牛客挑战赛38 - A - 多边形与圆

题目链接：https://ac.nowcoder.com/acm/contest/4643/A

题意：一个半径为r的空心圆，内部有一个n个点的凸多边形，这个多边形在圆壳的内部滚动。多边形顶点按照逆时针顺序给出，保证每一个顶点都有机会接触圆壳。

起初，1号点,2号点一定在圆上，初始以1号点为轴心、然后依次以2, 3, ..., n号点为轴心“滚动”。具体地讲，在以i号点为轴心“滚动”时，多边形将保持i号点不动，并以该点为中心开始顺时针旋转，直到i+1号点接触圆为止，然后更换轴心，继续“滚动”。

求多边形从初始开始滚动、直到1号点再次到达圆上成为轴心为止，1号点在整个滚动过程中所经过的路程是多少。

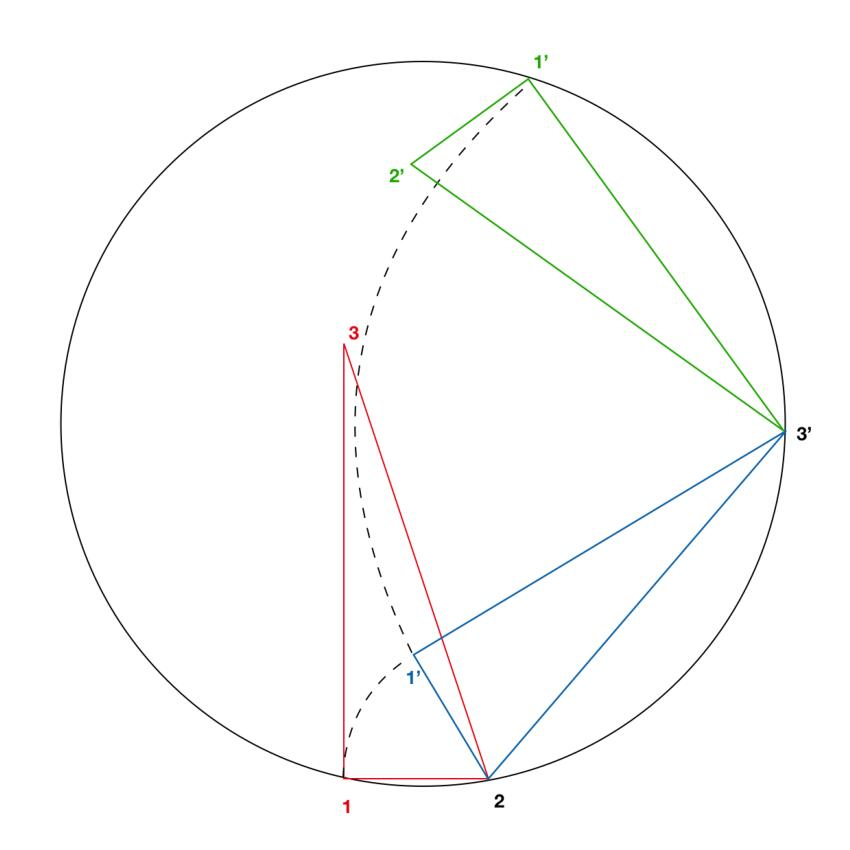
题解：画了很久之后才发现，第i次旋转的圆心角，可以由第i个点、第i+1个点、第i+2个点的组成的两条弦算出弦所对的圆心角（用余弦定理算），然后用圆心角算出弦与圆心组成的等腰三角形的底角（或者直接用余弦定理算出底角）。然后旋转角就是这两个底角的和减去第i+1个点所在的多边形的角。旋转半径不见得一定会是多边形的边，而是第1个点和第i+1个点的连线。注意旋转n-1次后第1个点会和第n个点重新出现在圆上。

const double PI = acos(-1.0);

double x[105], y[105];

double distance(int i, int j) {
    return sqrt((x[i] - x[j]) * (x[i] - x[j]) + (y[i] - y[j]) * (y[i] - y[j]));
}

double angle(int i, int j, int k) {
    double p1x = x[i] - x[j], p1y = y[i] - y[j];
    double p2x = x[k] - x[j], p2y = y[k] - y[j];
    double cosval = (p1x * p2x + p1y * p2y) / (sqrt(p1x * p1x + p1y * p1y) * sqrt(p2x * p2x + p2y * p2y));
    return acos(cosval);
}

int main() {
    int n, r;
    scanf("%d%d", &n, &r);
    for(int i = 1; i <= n; ++i)
        scanf("%lf%lf", &x[i], &y[i]);
    x[n + 1] = x[1], y[n + 1] = y[1];
    x[n + 2] = x[2], y[n + 2] = y[2];
    double sum = 0;
    for(int i = 1; i <= n - 1; ++i) {
        double alpha = acos(distance(i, i + 1) / (2.0 * r));
        double beta = acos(distance(i + 1, i + 2) / (2.0 * r));
        double A = alpha + beta - angle(i, i + 1, i + 2);
        sum += A * distance(1, i + 1);
    }
    printf("%.12f\n", sum);
    return 0;
}