2019-2020 ICPC, Asia Jakarta Regional Contest (Online Mirror, ICPC Rules, Teams Preferred)
题目链接:https://codeforces.com/contest/1252
A - Copying Homework
题意:给一个[1,n]的排列A,构造另一个排列B,到它的距离最大。两个排列的距离,是每个对应位置的元素的差的绝对值之和。
题解:画在数轴上面很容易发现,例如n=6时,[1,2]这一段只会最多经过1次,[2,3]这一段只会最多经过2次,[3,4]这一段只会最多经过3次……然后看一下好像和奇偶性也没什么关系。而Bi=n+1-Ai恰好是上面的最大值的一种构造。
C - Even Path
题意:给一个数字maze,它的生成规则是A[i][j]=R[i]+C[j],给出R数组和C数组。定义“偶数路径”为一条所有点权都是偶数的路径。每次询问两个点,保证起点和终点必为偶数格子,回答是否存在至少一条偶数路径连接他们。
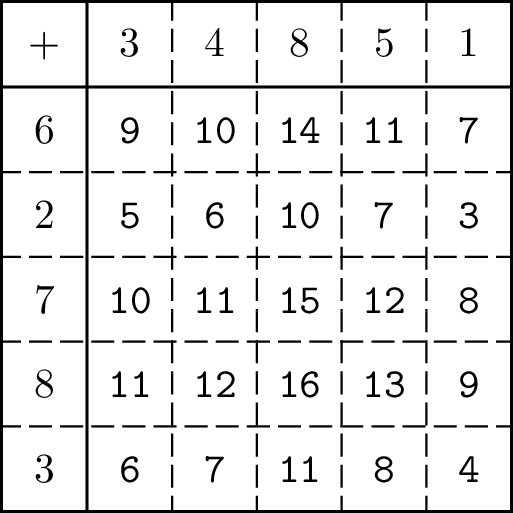
题解:并查集?比上一题还水?但是数据范围是蛮大的,不能这样暴力。考虑相邻的两格是否能互相到达,由于对应位置由相同的C[j]贡献,所以当C[j]是奇数时,两个同为奇数的R[i]与R[i+1]就同为偶数,当C[j]是偶数时,两个同为偶数的R[i]与R[i+1]也同为偶数。假如把偶数格子染黑色,把奇数格子染白色,那么从上面的结果就感觉到相邻两行要么就是相同颜色要么就是相反颜色。看看上面这个图貌似是这个意思。所以得到一个结论,假如从起点所在的行和终点所在的行之间存在某次奇偶交替,则无解,列同理。假如不存在交替是否一定有解?答案显然是肯定的(因为起点和终点必为偶数格子,而行和列都没发生奇偶交替,所以随便走过去都可以)。
所以做两个前缀和表示奇偶交替的次数,然后验证这中间没有奇偶交替即可。
注意:是要求中间的奇偶交替的次数,而不是奇数的次数,所以是求出奇偶性之后再做一次“差分”,然后统计“差分”的前缀和。注意这里确实不需要-1。显然“差分”的前缀和并不是原数组,因为这里的“差分”只是代表奇偶性翻转。
int r[100005];
int R[100005];
int c[100005];
int C[100005];
void test_case() {
int n, q;
scanf("%d%d", &n, &q);
for(int i = 1; i <= n; ++i) {
scanf("%d", &r[i]);
r[i] = r[i] & 1;
R[i] = (r[i] != r[i - 1]);
R[i] += R[i - 1];
}
for(int i = 1; i <= n; ++i) {
scanf("%d", &c[i]);
c[i] = c[i] & 1;
C[i] = (c[i] != c[i - 1]);
C[i] += C[i - 1];
}
while(q--) {
int r1, c1, r2, c2;
scanf("%d%d%d%d", &r1, &c1, &r2, &c2);
if(r1 > r2)
swap(r1, r2);
if(c1 > c2)
swap(c1, c2);
if(R[r2] - R[r1] == 0 && C[c2] - C[c1] == 0)
puts("YES");
else
puts("NO");
}
}
*H - Twin Buildings
题意:要在 \(n\) 块长方形地上造两栋形状一样(长和宽一样,可以旋转90°)的建筑物,建筑物可以建在两块不同的地上,或者同一块地上。为了风水好,他们的边必须与地面的边平行。求一栋建筑的最大的面积。
题解:首先,答案不少于每块地的面积的一半,这就是两栋建在同一块地上的最大值。然后,对于某块地而言,要建一个最大的建筑物,应该就是拿另一块地和这块地取交或者旋转90°取交的最大值。可惜不能 \(n^2\) 搞。一个很显然的思路,就是把每块地和它的旋转90°的结果放进一个数据结构里,这个数据结构可以回答某块地作为A时,这个数据结构中的地作为B时的最大的面积。然后轮到这块地做A的时候,就从数据结构里面暂时移除它和它的旋转90°。所有比A长的矩形,答案就取A的长和AB的宽的最小值,所以就在比A长的矩形中求最大的宽。所有比A宽的矩形,答案就取A的宽和AB的长的最小值,所以就在比A宽的矩形中求最大的长。剩下的矩形一定是长比A小,宽也比A小的,答案就是B的面积的两倍。前面两种情况可以用平衡树或者权值线段树维护。对于第三种情况,可以直接跳过,等待A和B交换位置的时候就会被统计。
需要注意的是,权值线段树的每个叶子需要保存前三大,因为每次询问前会至多移除两个。
但是会不会有更简单的做法呢?
struct SegmentTree {
#define ls (o<<1)
#define rs (o<<1|1)
static const int MAXN = 200000;
int ma1[(MAXN << 2) + 5];
int ma2[MAXN + 5];
int ma3[MAXN + 5];
int cma1[MAXN + 5];
int cma2[MAXN + 5];
void PushUp(int o) {
ma1[o] = max(ma1[ls], ma1[rs]);
}
void Build(int o, int l, int r) {
if(l == r) {
ma1[o] = -INF;
ma2[l] = -INF;
ma3[l] = -INF;
cma1[l] = -INF;
cma2[l] = -INF;
} else {
int m = l + r >> 1;
Build(ls, l, m);
Build(rs, m + 1, r);
PushUp(o);
}
}
void Insert(int o, int l, int r, int p, int v) {
if(l == r) {
if(v > ma3[l]) {
ma3[l] = v;
if(ma3[l] > ma2[l]) {
swap(ma3[l], ma2[l]);
cma2[l] = ma2[l];
if(ma2[l] > ma1[o]) {
swap(ma2[l], ma1[o]);
swap(cma2[l], cma1[l]);
}
}
}
} else {
int m = l + r >> 1;
if(p <= m)
Insert(ls, l, m, p, v);
if(p >= m + 1)
Insert(rs, m + 1, r, p, v);
PushUp(o);
}
}
void Remove(int o, int l, int r, int p, int v) {
if(l == r) {
if(v <= ma3[l])
return;
if(v == ma2[l]) {
ma2[l] = ma3[l];
return;
}
if(v == ma1[o]) {
ma2[l] = ma3[l];
ma1[o] = ma2[l];
return;
}
exit(-1);
} else {
int m = l + r >> 1;
if(p <= m)
Remove(ls, l, m, p, v);
if(p >= m + 1)
Remove(rs, m + 1, r, p, v);
PushUp(o);
}
}
void UndoRemove(int o, int l, int r, int p) {
if(l == r) {
ma1[o] = cma1[l];
ma2[l] = cma2[l];
} else {
int m = l + r >> 1;
if(p <= m)
UndoRemove(ls, l, m, p);
if(p >= m + 1)
UndoRemove(rs, m + 1, r, p);
PushUp(o);
}
}
int Query(int o, int l, int r, int ql, int qr) {
if(ql <= l && r <= qr) {
return ma1[o];
} else {
int m = l + r >> 1;
int res = -INF;
if(ql <= m)
res = Query(ls, l, m, ql, qr);
if(qr >= m + 1)
res = max(res, Query(rs, m + 1, r, ql, qr));
return res;
}
}
#undef ls
#undef rs
} st;
int L[100005];
int idL[100005];
int W[100005];
int idW[100005];
int V[200005], vtop;
void show() {
for(int i = 1; i <= vtop; ++i)
printf("%d ", st.Query(1, 1, vtop, i, i));
puts("");
for(int i = 1; i <= vtop; ++i)
printf("%d ", st.ma2[i]);
puts("");
for(int i = 1; i <= vtop; ++i)
printf("%d ", st.ma3[i]);
puts("\n---");
}
void test_case() {
int n;
scanf("%d", &n);
vtop = 0;
ll sumarea = 0;
for(int i = 1; i <= n; ++i) {
scanf("%d%d", &L[i], &W[i]);
sumarea = max(sumarea, 1ll * L[i] * W[i]);
V[++vtop] = L[i];
V[++vtop] = W[i];
}
sort(V + 1, V + 1 + vtop);
vtop = unique(V + 1, V + 1 + vtop) - (V + 1);
for(int i = 1; i <= n; ++i) {
idL[i] = lower_bound(V + 1, V + 1 + vtop, L[i]) - V;
idW[i] = lower_bound(V + 1, V + 1 + vtop, W[i]) - V;
}
st.Build(1, 1, vtop);
for(int i = 1; i <= n; ++i) {
st.Insert(1, 1, vtop, idL[i], W[i]);
st.Insert(1, 1, vtop, idW[i], L[i]);
}
for(int i = 1; i <= n; ++i) {
st.Remove(1, 1, vtop, idL[i], W[i]);
st.Remove(1, 1, vtop, idW[i], L[i]);
sumarea = max(sumarea, 2ll * W[i] * min(st.Query(1, 1, vtop, idW[i], vtop), L[i]));
sumarea = max(sumarea, 2ll * L[i] * min(st.Query(1, 1, vtop, idL[i], vtop), W[i]));
st.UndoRemove(1, 1, vtop, idL[i]);
st.UndoRemove(1, 1, vtop, idW[i]);
}
printf("%lld.%c\n", sumarea / 2, "05"[sumarea % 2 == 1]);
}
看了标签是贪心,我都惊呆了。假如是两个有包含关系的矩形,则是取小的那个矩形,否则设矩形1为 \(L_1\times W_1\) 矩形2为 \(L_2\times W21\) ,且 \(L_1>L_2\) 且 \(W_1<W_2\) 且 \(L_1\geq W_1\) 且 \(L_2\geq W_2\) ,若长对长,宽对宽,结果为 \(L_2\times W_1\) ,若长对宽,宽对长,则是 \(min(L_1,W_2)\times min(L_2,W_1)=W_2\times W_1\leq L_2\times W_1\) 所以一定是长对长,宽对宽。按长排序,每个矩形考虑排在其后面的矩形,贡献长的一定是它本身,而贡献宽的是一个后缀最大值和它本身的宽的最小值。
pii a[100005];
void test_case() {
int n;
scanf("%d", &n);
ll ans = 0;
for(int i = 1; i <= n; ++i) {
int x, y;
scanf("%d%d", &x, &y);
if(x < y)
swap(x, y);
a[i] = {x, y};
ans = max(ans, 1ll * x * y);
}
sort(a + 1, a + 1 + n);
int maxW = a[n].second;
for(int i = n - 1; i >= 1; --i) {
ans = max(ans, 2ll * a[i].first * min(a[i].second, maxW));
maxW = max(maxW, a[i].second);
}
printf("%lld.%c\n", ans / 2, "05"[ans % 2 == 1]);
}
反思:引入一点假设,貌似可以观察出规律。且得到奇怪的知识各边平行的两个矩形的面积最大的交,为长边对长边,短边对短边的结果。





