Codeforces Round #619 (Div. 2)

题目链接：https://codeforces.com/contest/1301

A - Three Strings

水题

B - Motarack's Birthday

题意：给一个数组，至少一个位置是空的，要求给所有的空的位置填上同一个数字x，使得相邻两个数字的差最小，有多种x输出任意一种。

题解：显然相邻两个数字的差，要么是固定的两个数字提供的，要么就是一个数字和一个空位提供的（两个空位之间是没有差的）。只需要找到空位两边的最大值和最小值，这个时候x肯定是选择这俩的平均值（假如有两个平均值，选择任意一个）。

C - Ayoub's function

题意：在n个数字0中，选恰好m个变成1。使得这个数字字符串中，包含至少一个1的子串最多。输出最多有多少个包含至少一个1的子串。

题解：子串个数是恒定的，所以等价于要全是0的子串最少。打表发现貌似是平均分配0的情况下满足题意。写了一个这个东西。

应该准确一点的证明是这样：考虑两个全为0的子串，总长为l，其中一个长为x，那么他们贡献的全为0的子串的个数就是： \(f(x)=\frac{1}{2}x(x+1)+\frac{1}{2}(l-x)(l-x+1)\) 即 \(f(x)=\frac{1}{2}(2x^2-2lx+l^2+l)\) 意思就是尽可能平均的时候取到最小值。

void test_case() {
    ll n, k;
    scanf("%lld%lld", &n, &k);
    if(k == 0) {
        puts("0");
        return;
    }
    ll ans = (n + 1) * n / 2;
    if(n == k) {
        printf("%lld\n", ans);
        return;
    }
    ll cn = n - k;
    if(cn <= k) {
        printf("%lld\n", ans - cn);
        return;
    }
    ++k;
    ll m1 = cn / k;
    ll m2 = m1 + 1;
    ll c2 = cn % k;
    ll c1 = (cn - (c2 * m2)) / m1;
//    printf("m1=%lld m2=%lld\n", m1, m2);
//    printf("c1=%lld c2=%lld\n", c1, c2);
//    printf("cn=%lld sum=%lld\n", cn, c1 * m1 + c2 * m2);
    ans -= ((m1 + 1) * m1) / 2 * c1;
    ans -= ((m2 + 1) * m2) / 2 * c2;
    printf("%lld\n", ans);
}

总结：注意有k个1，是把0分成k+1份，注意特判不够分的情况，这时平均值的下整是0，有可能会RE：dividing by zero。

*D - Time to Run

题意：给一个 \(n*m(1\leq n \leq 500,1\leq m\leq 500)\) 个格子，相邻格子x,y之间有两条边，分别是x->y和y->x。限制：每条边至多经过1次，且起始格子必须在左上角，求是否能恰好走k条边。

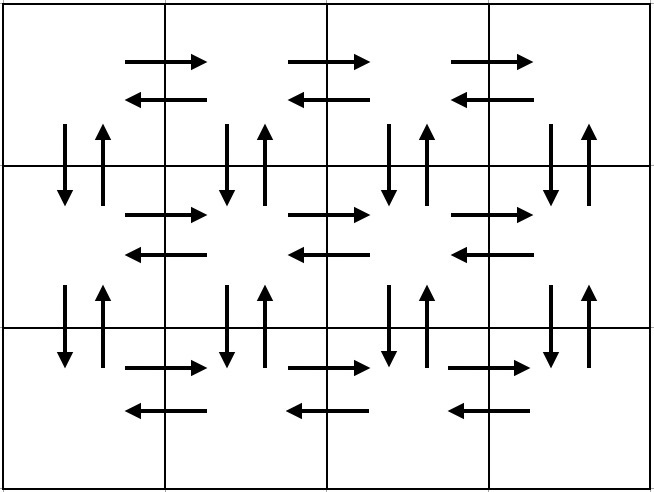
题解：不妨设 \(m>=n\) 一开始想到一种策略，就是逐行扫描，每次走到最右然后折返到最左，再向下移动，这样至多移动 \(n*(m-1)*2+(n-1)\) 次，写出了一种（蠢的，浪费步骤的）实现，交上去WA了。想到左右向的边已经充分利用了，但是只用了向下的一条完整的边。考虑上面的构造肯定是不优的，因为我到了左下角之后至少还能向上走回去。再想想可以在回来的时候逐列扫描，也就是每次先向上走，再向下走，到底边之后再向左移动。发现这样的构造是可以遍历所有的边的，所以答案就是这种遍历所有边的构造。

写的时候注意，限制只能有3000行输出，平均给每行每列就只有3行输出，一开始还搞什么/4又%4的，白白浪费步骤，上面这个构造中每行每列至多使用了3行输出进行扫描。去掉/4又%4之后还要注意，每次移动不能是0格。

pair<int, char> ans[3005];
int atop;

void add(int &k, int x, char c) {
    if(x) {
        ans[++atop] = {x, c};
        k -= x;
    }
}

void test_case() {
    int n, m, k;
    scanf("%d%d%d", &n, &m, &k);
    if(k > 4 * n * m - 2 * n - 2 * m) {
        puts("NO");
        return;
    }

    atop = 0;
    int y = 1;
    while(k) {
        add(k, min(m - 1, k), 'R');
        if(y == n)
            break;
        add(k, min(m - 1, k), 'L');
        add(k, min(1, k), 'D');
        ++y;
    }
    int x = m;
    while(k) {
        add(k, min(n - 1, k), 'U');
        add(k, min(n - 1, k), 'D');
        add(k, min(1, k), 'L');
        --x;
    }

    puts("YES");
    printf("%d\n", atop);
    for(int i = 1; i <= atop; ++i)
        printf("%d %c\n", ans[i].first, ans[i].second);
}