模板 - 数学 - 组合数学 - 置换群

Burnside引理：
等价类的个数就是旋转不同角度的不动点的数量的平均。

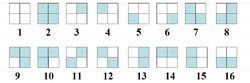
4个正方形，涂2种颜色，涂色方法显然有2^4=16种，由旋转组成的等价类的个数为：

逆时针旋转0°：
16种自己和自己等价
逆时针旋转90°：
只有全白和全黑旋转后和自己等价。
逆时针旋转180°：
只有全白和全黑，主对角黑和副对角黑4种和自己等价。
逆时针旋转270°：
只有全白和全黑旋转后和自己等价。

等价类的个数为：(16+2+4+2)/4=6种

Polya定理：
n个结点的环，染m种颜色的，只经过旋转的本质不同的涂色方法数。

ll Polya(ll n, ll m) {
    ll res = 0;
    for(ll i = 1; i * i <= n; i++) {
        if(n % i)
            continue;
        res += phi(i) * qpow(m, n / i - 1);
        if(i * i != n)
            res += phi(n / i) * qpow(m, i - 1);
    }
    res %= mod;
    return res;
}