求二维整型数组的所有子数组的和的最大子数组

 //注：本次小队成员为：王友军，白宇乾，黄瑞玻；原因与上一次相同，请见谅。

本次作业是关于二维整型数组的最大子数组的求解，相比第一次的一维数组来说，确实难了些。经过我们的苦思冥想，想了很多设计思路，但是都是存在着很多问题；在没有别的好的方法选择之后，我们只能选择了最基本的：枚举法进行求解。设计思路：

1.确定二维数组的所有子数组的数量，并用一个一维整型数组sum[]存储;

2.从第一个元素开始，以第一个元素为子数组的起始元素，将整个数组遍历,每得到一个二维子数组，就存储到sum[]中；然后以第二个元素为开始；依此类推，直到最后一个元素结束。

3.然后求出sum[]数组中的最大元素，则该元素就是最大的子数组和。

程序代码：

#include<iostream>
using namespace std;

int main()
{
    int m,n;
    cout << "请输入二维数组的行和列：";
    cin >> n>> m;
    //定义一个可变长二维数组;
    int** a;
    a = new int*[n];
    for (int i = 0; i <= n; i++)
    {
        a[i] = new int[m];
    }
    //定义一个存储二维数组所有子数组的可变长一维数组;
    int *sum=new int [m*(m+1)*n*(n+1)/4];
    for (int i = 0; i < m*(m + 1)*n*(n + 1) / 4; i++)
    {
        sum[i] = 0;
    }
    int t = 0;
    cout << "输入数组的值：" << endl;
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            cin >> a[i][j];
        }
    }
    //用枚举法将所有子数组的和求出，放到sum数组里;
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            for (int p = i; p < n; p++)
            {
                for (int q = j; q < m; q++)
                {
                    for (int y = i; y <= p; y++)
                    {
                        for (int x = j; x <= q; x++)
                        {
                            //求子数组和;
                            sum[t] = sum[t] + a[y][x];
                        }
                    }
                    t++;
                }
            }
        }
    }
    //求最大子数组;
    for (int i = 0; i < m*(m + 1)*n*(n + 1) / 4; i++)
    {
        if (sum[0] < sum[i])
        {
            sum[0] = sum[i];
        }
    }
    cout<< "最大子数组的和为:"<<sum[0] << endl;
    system("pause");
    return 0;
}

测试截图：

 

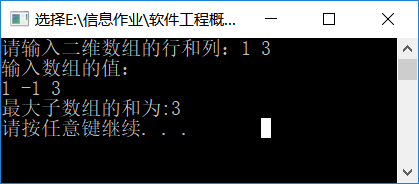
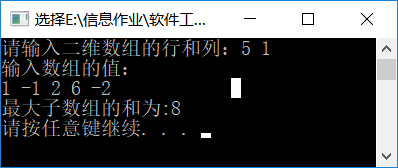
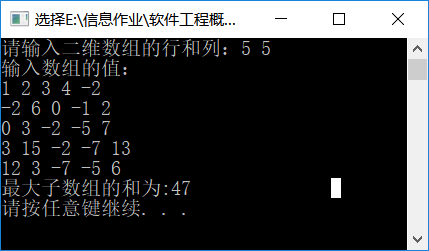
小组成员：