POJ 1486 Sorting Slides（二分图完全匹配必须边）题解

题意：给你n张照片的范围，n个点的坐标，问你能唯一确定那几个点属于那几张照片，例如样例中4唯一属于A，2唯一属于C，1唯一属于B，3唯一属于C

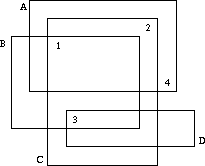
思路：进行二分图完全匹配，怎么判断唯一属于？匹配完之后删掉某一条匹配边再跑一次二分图匹配，如果还能完全匹配，那么就不是唯一，反之唯一。

代码：

#include<set>
#include<map>
#include<stack>
#include<cmath>
#include<queue>
#include<vector>
#include<string>
#include<cstdio>
#include<cstring>
#include<sstream>
#include<iostream>
#include<algorithm>
typedef long long ll;
using namespace std;
const int maxn = 100 + 10;
const int MOD = 1e9 + 7;
const int INF = 0x3f3f3f3f;
struct node{
    int x1, x2, y1, y2;
}p[maxn];
struct Node{
    int x, y;
}a[maxn];
struct Edge{
    int to, next;
}edge[maxn * 4];
int g[maxn][maxn], linker[maxn], ans[maxn], n;
bool used[maxn];
bool dfs(int u){
    for(int v = 0; v < 2 * n; v++){
        if(g[u][v] && !used[v]){
            used[v] = true;
            if(linker[v]== -1 || dfs(linker[v])){
                linker[v] = u;
                return true;
            }
        }
    }
    return false;
}
int hungary(){
    int res = 0;
    memset(linker, -1, sizeof(linker));
    for(int u = 0; u < 2 * n; u++){
        memset(used, false, sizeof(used));
        if(dfs(u)) res++;
    }
    return res;
}
bool inside(node m, Node n){
    if(n.x > m.x1 && n.x < m.x2 && n.y > m.y1 && n.y < m.y2) return true;
    return false;
}
int main(){
    int ca = 1;
    while(~scanf("%d", &n) && n){
        for(int i = 0; i < n; i++){
            scanf("%d%d%d%d", &p[i].x1, &p[i].x2, &p[i].y1, &p[i].y2);
        }
        memset(g, 0, sizeof(g));
        for(int i = 0; i < n; i++){
            scanf("%d%d", &a[i].x, &a[i].y);
            for(int j = 0; j < n; j++){
                if(inside(p[j], a[i])){
                    g[i][n + j] = g[n + j][i] = 1;
                }
            }
        }
        printf("Heap %d\n", ca++);
        int ret = hungary();
        memcpy(ans, linker, sizeof(ans));
        if(ret != 2 * n) printf("none\n");
        else{
            bool ok = false;
            for(int i = n; i < 2 * n; i++){
                g[i][ans[i]] = g[ans[i]][i] = 0;
                ret = hungary();
                if(ret == 2 * n) continue;
                printf("%s(%c,%d)", ok == true? " " : "",'A' + (i - n), ans[i] + 1);
                ok = true;
                g[i][ans[i]] = g[ans[i]][i] = 1;
            }
            if(!ok) printf("none\n");
            else printf("\n");
        }
        printf("\n");
    }
    return 0;
}