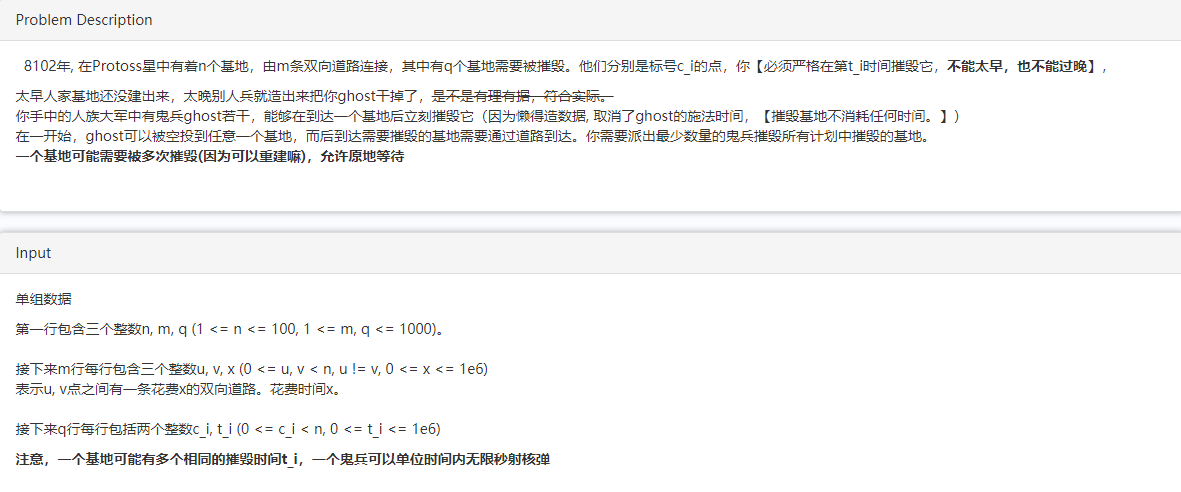
FJUT3591 侦测到在途的聚变打击（最小不可相交路径覆盖）题解

题意：给你n个点，点间m条路，给出在每条路要走的时间。现在有q个任务，要摧毁q个点，每次提供ci和ti表示在时间ti摧毁点ci（必须正好在时间ti才能摧毁），每个点可能需要多次摧毁（同一时间能在同一个点摧毁无数个点），允许在某个点停留任意时间。问现在要派几个小兵去摧毁点，最少派几个？

原题：

思路：小兵既然能无限停留在某个点，那么我能从t小的点走到t大的点并摧毁t大的那个点的条件，应该是这两点间最短路小于等于时间差。所以我们直接Floyd跑多源最短路。但是他只需要摧毁q个可能重复的点，不是摧毁整张图，那么我们可以这么想，把q次摧毁看成q个单独的点，每个点的距离就是他们所代表的点之间的最短路（显然相同两个点距离0），然后这样拆点得到二分图，跑最小可相交路径覆盖。

参考：有向无环图（DAG）的最小路径覆盖

代码：

#include<set>
#include<map>
#include<stack>
#include<cmath>
#include<queue>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
typedef long long ll;
using namespace std;
const int maxn = 10000 + 10;
const int seed = 131;
const ll MOD = 1e9 + 7;
const int INF = 0x3f3f3f3f;
struct Edge{
    int v, next;
}edge[maxn * 100];
int head[maxn], tot;
ll mp[105][105];
void addEdge(int u, int v){
    edge[tot].v = v;
    edge[tot].next = head[u];
    head[u] = tot++;
}
void init(){
    memset(head, -1, sizeof(head));
    memset(mp, INF, sizeof(mp));
    tot = 0;
}
void floyd(int n){
    for(int k = 1; k <= 100; k++){
        for(int i = 1; i <= 100; i++){
            for(int j = 1; j <= 100; j++){
                if(mp[i][j] > mp[i][k] + mp[k][j]){
                    mp[i][j] = mp[i][k] + mp[k][j];
                }
            }
        }
    }
}
int cy[maxn];
bool vis[maxn];
bool dfs(int u){
    for(int i = head[u]; i != -1; i = edge[i].next){
        int v = edge[i].v;
        if(vis[v]) continue;
        vis[v] = true;
        if(cy[v] == -1 || dfs(cy[v])){
            cy[v] = u;
            return true;
        }
    }
    return false;
}
int solve(int n){
    int ret = 0;
    memset(cy, -1, sizeof(cy));
    for(int i = 1;i <= n; i++){
        memset(vis, 0, sizeof(vis));
        ret += dfs(i);
    }
    return ret;
}
int c[maxn], t[maxn];
int main(){
    int n, m, q;
    init();
    scanf("%d%d%d", &n, &m, &q);
    int u, v;
    ll x;
    for(int i = 0; i < m; i++){
        scanf("%d%d%lld", &u, &v, &x);
        u++, v++;
        mp[u][v] = mp[v][u] = min(mp[u][v], x);
    }
    for(int i = 1; i <= 100; i++)
        mp[i][i] = 0;
    floyd(n);
    for(int i = 1; i <= q; i++)
        scanf("%d%d", &c[i], &t[i]), c[i]++;
    for(int i = 1; i <= q; i++){
        for(int j = 1; j <= q; j++){
            if(i == j) continue;
            if(t[j] >= t[i] && mp[c[i]][c[j]] <= (t[j] - t[i])){
                addEdge(i, j + q);
            }
        }
    }
    printf("%d\n", q - solve(2 * q));
    return 0;
}