sha2-512算法实现原理深剖
一、基本介绍
SHA (Security Hash Algorithm) 是美国的 NIST 和 NSA 设计的一种标准的 Hash 算法,SHA 用于数字签名的标准算法的 DSS 中,也是安全性很高的一种 Hash 算法。
SHA-1 是第一代 SHA 算法标准,后来的 SHA-224、SHA-256、SHA-384 和 SHA-512 被统称为 SHA-2。本文介绍SHA2-512算法的实现原理。
二、实现原理
有关 SHA2-512 算法详情请参见 NIST.FIPS.180-4 。

SHA2-512是SHA2-256的改进版,其算法没变,只是分块大小由原来的512bits(32bits*16)改为1024bits(64bits*16),初始值及运算由原来的32位改为64位比特。
NIST.FIPS.180-4 是SHA2-512算法的官方文档,(建议了解SHA2-512算法前,先了解下SHA2-256 sha2-256算法实现原理深剖 )其实现原理共分为5步:
第1步:字节填充(Append Padding Bytes)
数据先补上1个1比特,再补上k个0比特,使得补位后的数据比特数(n+1+k)满足(n+1+k) mod 1024 = 896,k取最小正整数。
第2步:追加长度信息(Append Length)
数据比特位的数据长度追加到最后16字节中。
第3步:初始化MD Buffer(Initialize MD Buffer)
这一步最简单了,定义H0~H7八个8字节数组,分别赋初值即可。
uint64_t H0 = 0x6A09E667F3BCC908; uint64_t H1 = 0xBB67AE8584CAA73B; uint64_t H2 = 0x3C6EF372FE94F82B; uint64_t H3 = 0xA54FF53A5F1D36F1; uint64_t H4 = 0x510E527FADE682D1; uint64_t H5 = 0x9B05688C2B3E6C1F; uint64_t H6 = 0x1F83D9ABFB41BD6B;
uint64_t H7 = 0x5BE0CD19137E2179;
第4步:处理消息块(Process Message in 16-Byte Blocks)
这个是SHA2-512算法最核心的部分了,对第2步组装数据进行分块依次处理。

第5步:输出(Output)
这一步也非常简单,只需要将计算后的H0、H1、H2、H3、H4、H5、H6、H7进行拼接输出即可。
三、示例讲解
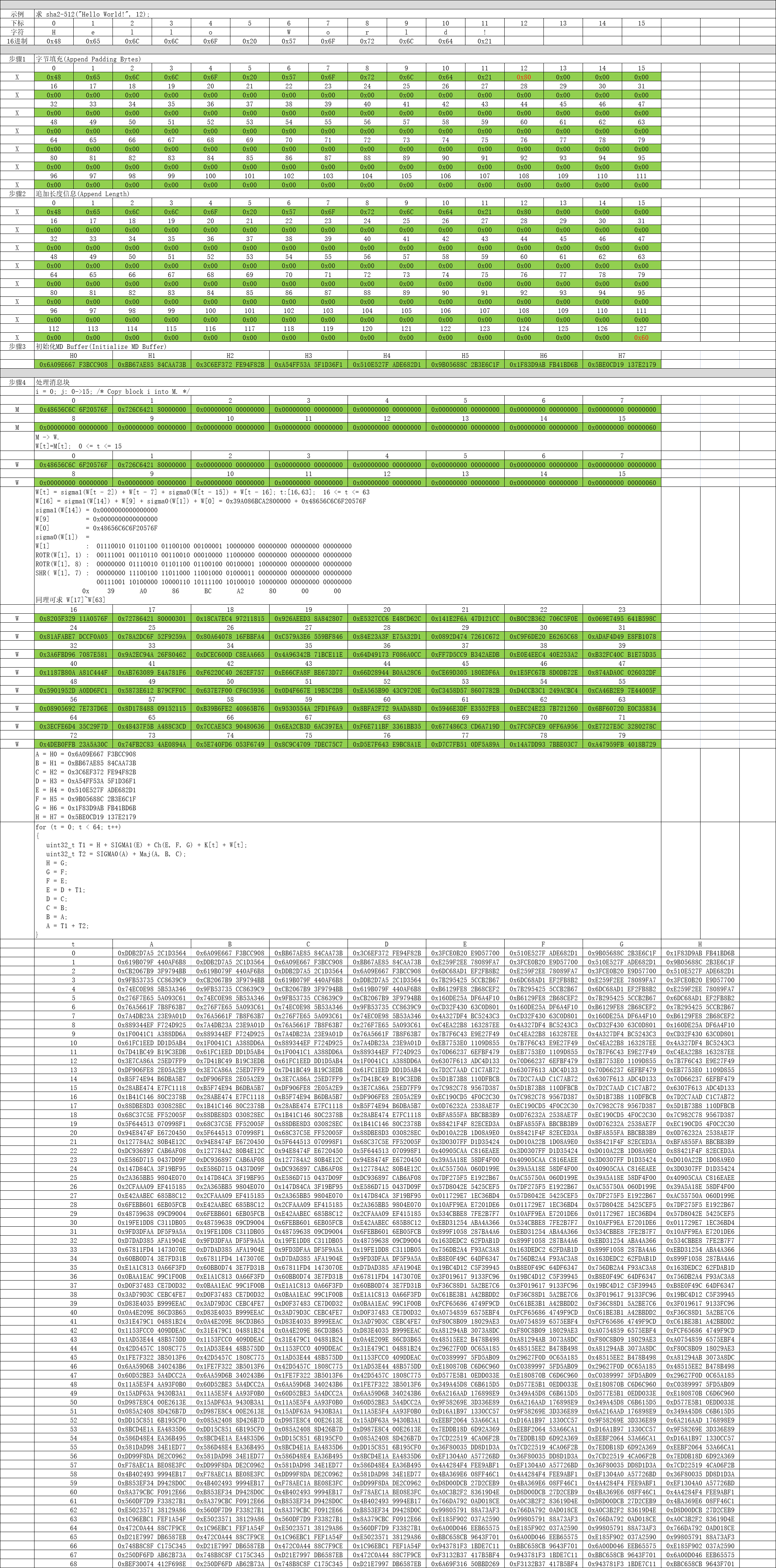
四、代码实现
以下为C/C++代码实现:
#include <string.h>
#include <stdio.h>
#define HASH_BLOCK_SIZE 128 /* 1024 bits = 128 bytes */
#define HASH_LEN_SIZE 16 /* 128 bits = 16 bytes */
#define HASH_LEN_OFFSET 112 /* 128 bytes - 16 bytes */
#define HASH_ROUND_NUM 80
typedef unsigned char uint8_t;
typedef unsigned short int uint16_t;
typedef unsigned int uint32_t;
typedef unsigned long long uint64_t;
typedef struct
{
uint64_t high; /* high 64 bits */
uint64_t low; /* low 64 bits */
} uint128_t;
/* SHA512 Constants */
static const uint64_t K[HASH_ROUND_NUM] =
{
0x428A2F98D728AE22, 0x7137449123EF65CD, 0xB5C0FBCFEC4D3B2F, 0xE9B5DBA58189DBBC,
0x3956C25BF348B538, 0x59F111F1B605D019, 0x923F82A4AF194F9B, 0xAB1C5ED5DA6D8118,
0xD807AA98A3030242, 0x12835B0145706FBE, 0x243185BE4EE4B28C, 0x550C7DC3D5FFB4E2,
0x72BE5D74F27B896F, 0x80DEB1FE3B1696B1, 0x9BDC06A725C71235, 0xC19BF174CF692694,
0xE49B69C19EF14AD2, 0xEFBE4786384F25E3, 0x0FC19DC68B8CD5B5, 0x240CA1CC77AC9C65,
0x2DE92C6F592B0275, 0x4A7484AA6EA6E483, 0x5CB0A9DCBD41FBD4, 0x76F988DA831153B5,
0x983E5152EE66DFAB, 0xA831C66D2DB43210, 0xB00327C898FB213F, 0xBF597FC7BEEF0EE4,
0xC6E00BF33DA88FC2, 0xD5A79147930AA725, 0x06CA6351E003826F, 0x142929670A0E6E70,
0x27B70A8546D22FFC, 0x2E1B21385C26C926, 0x4D2C6DFC5AC42AED, 0x53380D139D95B3DF,
0x650A73548BAF63DE, 0x766A0ABB3C77B2A8, 0x81C2C92E47EDAEE6, 0x92722C851482353B,
0xA2BFE8A14CF10364, 0xA81A664BBC423001, 0xC24B8B70D0F89791, 0xC76C51A30654BE30,
0xD192E819D6EF5218, 0xD69906245565A910, 0xF40E35855771202A, 0x106AA07032BBD1B8,
0x19A4C116B8D2D0C8, 0x1E376C085141AB53, 0x2748774CDF8EEB99, 0x34B0BCB5E19B48A8,
0x391C0CB3C5C95A63, 0x4ED8AA4AE3418ACB, 0x5B9CCA4F7763E373, 0x682E6FF3D6B2B8A3,
0x748F82EE5DEFB2FC, 0x78A5636F43172F60, 0x84C87814A1F0AB72, 0x8CC702081A6439EC,
0x90BEFFFA23631E28, 0xA4506CEBDE82BDE9, 0xBEF9A3F7B2C67915, 0xC67178F2E372532B,
0xCA273ECEEA26619C, 0xD186B8C721C0C207, 0xEADA7DD6CDE0EB1E, 0xF57D4F7FEE6ED178,
0x06F067AA72176FBA, 0x0A637DC5A2C898A6, 0x113F9804BEF90DAE, 0x1B710B35131C471B,
0x28DB77F523047D84, 0x32CAAB7B40C72493, 0x3C9EBE0A15C9BEBC, 0x431D67C49C100D4C,
0x4CC5D4BECB3E42B6, 0x597F299CFC657E2A, 0x5FCB6FAB3AD6FAEC, 0x6C44198C4A475817
};
/* Swap bytes in 64 bit value. 0x0123456789ABCDEF -> 0xEFCDAB8967452301*/
#define __bswap_64(x) \
((((x) & 0xff00000000000000ull) >> 56) \
| (((x) & 0x00ff000000000000ull) >> 40) \
| (((x) & 0x0000ff0000000000ull) >> 24) \
| (((x) & 0x000000ff00000000ull) >> 8) \
| (((x) & 0x00000000ff000000ull) << 8) \
| (((x) & 0x0000000000ff0000ull) << 24) \
| (((x) & 0x000000000000ff00ull) << 40) \
| (((x) & 0x00000000000000ffull) << 56))
static uint64_t Ch(uint64_t X, uint64_t Y, uint64_t Z)
{
return (X & Y) ^ ((~X) & Z);
}
static uint64_t Maj(uint64_t X, uint64_t Y, uint64_t Z)
{
return (X & Y) ^ (X & Z) ^ (Y & Z);
}
/* 循环向右移动offset个比特位 */
static uint64_t ROTR(uint64_t X, uint64_t offset)
{
return (X >> offset) | (X << (64 - offset));
}
/* 向右移动offset个比特位 */
static uint64_t SHR(uint64_t X, uint64_t offset)
{
return X >> offset;
}
/* SIGMA0 */
static uint64_t SIGMA0(uint64_t X)
{
return ROTR(X, 28) ^ ROTR(X, 34) ^ ROTR(X, 39);
}
/* SIGMA1 */
static uint64_t SIGMA1(uint64_t X)
{
return ROTR(X, 14) ^ ROTR(X, 18) ^ ROTR(X, 41);
}
/* sigma0, different from SIGMA0 */
static uint64_t sigma0(uint64_t X)
{
return ROTR(X, 1) ^ ROTR(X, 8) ^ SHR(X, 7);
}
/* sigma1, different from SIGMA1 */
static uint64_t sigma1(uint64_t X)
{
return ROTR(X, 19) ^ ROTR(X, 61) ^ SHR(X, 6);
}
#define ASSERT_RETURN_INT(x, d) if(!(x)) { return d; }
/* 此处的inlen用int不合理 但我们只是研究学习算法 不作为实际应用 */
int sha2_512(unsigned char *out, const unsigned char* in, const int inlen)
{
ASSERT_RETURN_INT(out && in && (inlen >= 0), 1);
int i = 0, j = 0, t = 0;
// step 1: 字节填充(Append Padding Bytes)
// 数据先补上1个1比特,再补上k个0比特,使得补位后的数据比特数(n+1+k)满足(n+1+k) mod 1024 = 896,k取最小正整数
int iX = inlen / HASH_BLOCK_SIZE;
int iY = inlen % HASH_BLOCK_SIZE;
iX = (iY < HASH_LEN_OFFSET) ? iX : (iX + 1);
int iLen = (iX + 1) * HASH_BLOCK_SIZE;
unsigned char* X = malloc(iLen);
memcpy(X, in, inlen);
// 先补上1个1比特+7个0比特
X[inlen] = 0x80;
// 再补上(k-7)个0比特
for (i = inlen + 1; i < (iX * HASH_BLOCK_SIZE + HASH_LEN_OFFSET); i++)
{
X[i] = 0;
}
// step 2: 追加长度信息(Append Length) [此处inlen是按int处理的p[0~7]直接写死0 ]
uint8_t *pLen = X + (iX * HASH_BLOCK_SIZE + HASH_LEN_OFFSET);
uint64_t iTempLen = inlen << 3;
uint8_t *pTempLen = &iTempLen;
pLen[0] = 0; pLen[1] = 0; pLen[2] = 0; pLen[3] = 0;
pLen[4] = 0; pLen[5] = 0; pLen[6] = 0; pLen[7] = 0;
pLen[8] = pTempLen[7]; pLen[9] = pTempLen[6]; pLen[10] = pTempLen[5]; pLen[11] = pTempLen[4];
pLen[12] = pTempLen[3]; pLen[13] = pTempLen[2]; pLen[14] = pTempLen[1]; pLen[15] = pTempLen[0];
// Step 3. 初始化MD Buffer(Initialize MD Buffer)
uint64_t H0 = 0x6A09E667F3BCC908;
uint64_t H1 = 0xBB67AE8584CAA73B;
uint64_t H2 = 0x3C6EF372FE94F82B;
uint64_t H3 = 0xA54FF53A5F1D36F1;
uint64_t H4 = 0x510E527FADE682D1;
uint64_t H5 = 0x9B05688C2B3E6C1F;
uint64_t H6 = 0x1F83D9ABFB41BD6B;
uint64_t H7 = 0x5BE0CD19137E2179;
uint64_t M[HASH_BLOCK_SIZE / 8] = { 0 };
uint64_t W[HASH_ROUND_NUM] = { 0 };
// step 4: 处理消息块(Process Message in 64-Byte Blocks)
for (i = 0; i < iLen / HASH_BLOCK_SIZE; i++)
{
/* Copy block i into M. */
for (j = 0; j < HASH_BLOCK_SIZE; j = j + 8)
{
uint64_t k = i * HASH_BLOCK_SIZE + j;
M[j / 8] = ((uint64_t)X[k] << 56) | ((uint64_t)X[k + 1] << 48) | ((uint64_t)X[k + 2] << 40) | ((uint64_t)X[k + 3] << 32)
| ((uint64_t)X[k + 4] << 24) | ((uint64_t)X[k + 5] << 16) | ((uint64_t)X[k + 6] << 8) | (uint64_t)X[k + 7];
}
/* W[t]=M[t]; t:[0,15] */
for (t = 0; t <= 15; t++)
{
W[t] = M[t];
}
/* W[t] = sigma1(W[t - 2]) + W[t - 7] + sigma0(W[t - 15]) + W[t - 16]; t:[16,63] */
for (t = 16; t < HASH_ROUND_NUM; t++)
{
W[t] = sigma1(W[t - 2]) + W[t - 7] + sigma0(W[t - 15]) + W[t - 16];
}
uint64_t A = H0;
uint64_t B = H1;
uint64_t C = H2;
uint64_t D = H3;
uint64_t E = H4;
uint64_t F = H5;
uint64_t G = H6;
uint64_t H = H7;
for (t = 0; t < HASH_ROUND_NUM; t++)
{
uint64_t T1 = H + SIGMA1(E) + Ch(E, F, G) + K[t] + W[t];
uint64_t T2 = SIGMA0(A) + Maj(A, B, C);
H = G;
G = F;
F = E;
E = D + T1;
D = C;
C = B;
B = A;
A = T1 + T2;
}
H0 = H0 + A;
H1 = H1 + B;
H2 = H2 + C;
H3 = H3 + D;
H4 = H4 + E;
H5 = H5 + F;
H6 = H6 + G;
H7 = H7 + H;
}
// step 5: 输出
uint64_t* pOut = (uint8_t*)out;
pOut[0] = __bswap_64(H0);
pOut[1] = __bswap_64(H1);
pOut[2] = __bswap_64(H2);
pOut[3] = __bswap_64(H3);
pOut[4] = __bswap_64(H4);
pOut[5] = __bswap_64(H5);
pOut[6] = __bswap_64(H6);
pOut[7] = __bswap_64(H7);
free(X);
return 0;
}
int main()
{
unsigned char digest[64] = { 0 };
sha2_512(digest, "Hello World!", strlen("Hello World!"));
return 0;
}


