不常用的黑科技——「三元环」

万恶之源：

给定一张无重边、无自环的无向图（点数为$n$，边数为$m$，且$n,m$同阶），问有多少个无序三元组$(i,j,k)$，使得存在：

1. 有一条连接$i,j$的边

2. 有一条连接$j,k$的边

3. 有一条连接$k,i$的边

举个例子：

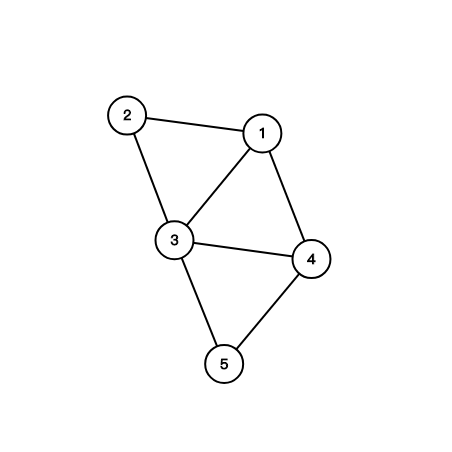
这张图中有三个三元环：$(1,2,3),(1,3,4),(3,4,5)$

有一个显然的基于度数的乱搞的做法（本人并没有写过……），可以在这里阅读到：jiachin_zhao [hdu 6184 Counting Stars](三元环计数)

这里介绍一种十分优秀的三元环计数方法：

首先要对所有的无向边进行定向，对于任何一条边，从度数大的点连向度数小的点，如果度数相同，从编号小的点连向编号大的点

此时这张图是一个有向无环图

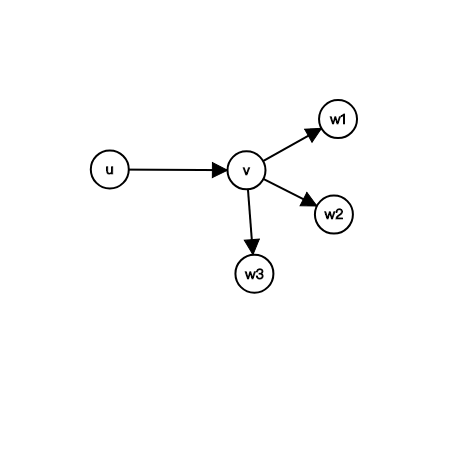
之后枚举每一个点$u$，然后将$u$的所有相邻的点都标记上“被$u$访问了”，然后再枚举$u$的相邻的点$v$，然后再枚举$v$的相邻的点$w$，如果$w$存在“被$u$访问了”的标记，那么$(u,v,w)$就是一个三元环了

而且每个三元环只会被计算一次

那么现在就只需要证明三件事：

1. 定向后的图是一个有向无环图

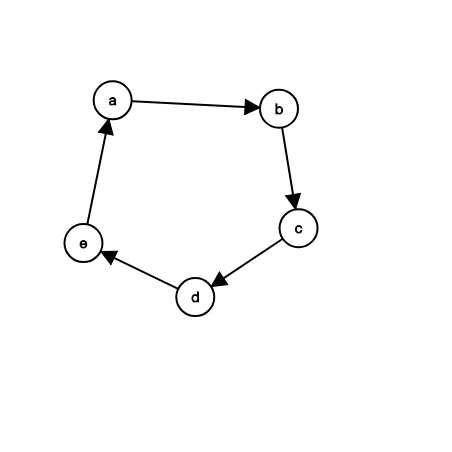
以上图为例，用$deg_u$表示$u$在原图中的度数，则$deg_a \ge deg_b \ge deg_c \ge deg_d \ge deg_e \ge deg_a$

既$deg_a=deg_b=deg_c=deg_d=deg_e=deg_a$

对于度数相同的点，是按照编号从小到大连边的，则$a \le b \le c \le d \le e \le a$

既$a=b=c=d=e$

然而点的编号是$1 \sim n$的全排列，因此不会产生如上的事情，既不存在环

由于这张图有向，而且没有环，因此这张图就是有向无环图

2. 时间复杂度是$O(m  \sqrt m)$（在此认为$n,m$同阶）

对于“打标记”这个操作，每个点都会将所有的出边遍历一遍，那么这里的时间复杂度为$O(n+m)$

对于访问$u$，然后访问$v$，然后访问$w$，可以这么考虑：对于每条边（$u \rightarrow v$），对时间复杂度的贡献为$out_v$​，其中$out_v$表示$v$的出边个数

这样就转化为了求$\sum_{i=1}^{n}out_i$

不妨将$out_v$分类讨论

1. $out_v \le \sqrt m$​，那么由于$u$连接$v$，因此$deg_u \ge deg_v$​，这样的uu的个数是$O(n)$的，因此这里的时间复杂度为$O(n \sqrt m)$

2. $out_v \gt \sqrt m$，那么由于$u$连接$v$，因此$deg_u \ge deg_v$，既$deg_u \gt \sqrt m$​，这样的$u$的个数是$O(\sqrt m)$的，因此这里的时间复杂度为$O(\sqrt m m)=O(m \sqrt m)$

因此时间复杂度为$O(n+m+n\sqrt m+m\sqrt m)=O(m \sqrt m)$

3. 每个三元环只会被统计一次

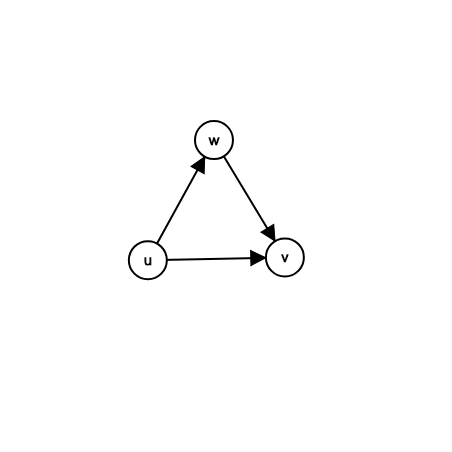
三元环在有向无环图上无非就长这样：

也只能且只会在$u$处被计算一次

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
vector<int> g[N];
int deg[N], vis[N], n, m, ans;
struct E { int u, v; } e[N * 3];
int main() {
    scanf("%d%d", &n, &m);
    for(int i = 1 ; i <= m ; ++ i) {
        scanf("%d%d", &e[i].u, &e[i].v);
        ++ deg[e[i].u], ++ deg[e[i].v];
    }
    for(int i = 1 ; i <= m ; ++ i) {
        int u = e[i].u, v = e[i].v;
        if(deg[u] < deg[v] || (deg[u] == deg[v] && u > v)) swap(u, v);
        g[u].push_back(v);
    }
    for(int x = 1 ; x <= n ; ++ x) {
        for(auto y: g[x]) vis[y] = x;
        for(auto y: g[x])
            for(auto z: g[y])
                if(vis[z] == x)
                    ++ ans;
    }
    printf("%d\n", ans);
}