JZOJ 5803. 【2018.8.12省选模拟】girls

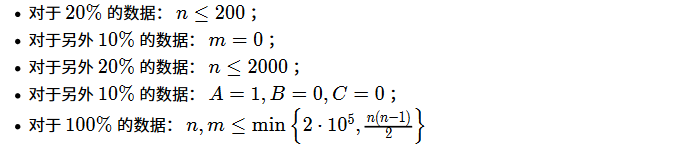
A,B,C<=1e6
保证冲突关系中的x不等于y
设$f(i)$表示不满足条件的对数至少有$i$对时的答案
则$ans=f(0)-f(1)+f(2)-f(3)$
稍微解释一下,如果$(0,1),(1,2)$属于不能在一起的集合的话
在$f(0)$中,$(0,1,2)$会被加上一遍
在$f(1)$中,$(0,1,2)$会被减去两遍,分别在$(0,1,*),(*,1,2)$中统计到
在$f(2)$中,$(0,1,2)$会被加上一遍
在$f(3)$中,不会计算到
然后成功将答案容斥对了
计算$f(0)$
枚举$0 \le i \le n-1$,统计$i$在每个位置(三种情况,$(j,k,i),(j,i,k),(i,j,k)$)上出现次数
1. 对于$(j,k,i)$,出现次数为$C_{i}^{2}$
2. 对于$(j,i,k)$,出现次数为$i \times (n - i - 1)$
3. 对于$(i,j,k)$,出现次数为$C_{n-i-1}^{2}$
然后乘上对应的系数(三种情况,$A \times i, B \times i, C \times i$),累加起来就是$f(0)$了
计算$f(1)$
直接枚举不合法关系$(x,y)$,分别讨论$(x,y,z),(x,z,y),(z,x,y)$三种情况
计算$f(2)$
对于不合法的关系$(x,y)$,视作$x$和$y$之间有一条无向边
每个点维护两个$vector$,分别存储与该点相连,编号小于该点的点,以及编号大于该点的点
这样一来至少有两对不合法的方案就一共有三种(假设当前枚举到了$x$,其中$(y,z)$是$x$相邻中的点)
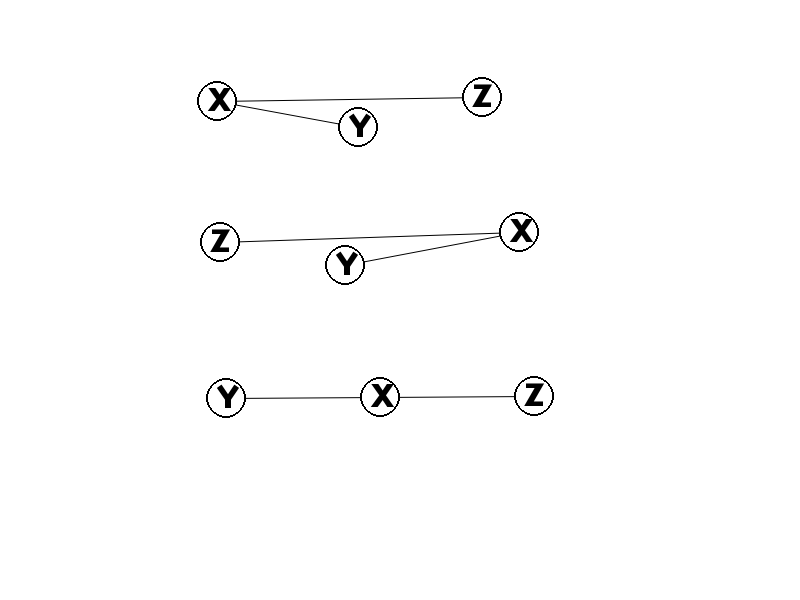
对于前两种情况,可以将两个$vector$排序后边计算前/后缀和,边统计答案
对于第三种情况,直接统计贡献即可
计算$f(3)$
即统计图上三元环的个数,方法如下:
1. 对于不合法关系$(x,y)$,连无向边$(x,y)$
2. 对于所有的无向边,将其定向:如果$u$和$v$的度数不相同,则边的方向为度数大的朝向度数小的,否则编号小的朝向编号大的,此时这张图是一个$DAG$
3. 开一个全局$vis$数组,大小为点的个数
4. 枚举了$x$,将$x$所有出点在$vis$数组中标为$1$
5. 枚举$x$的所有出点$y$,然后枚举所有出点$z$,如果$z$在$vis$数组中被标为$1$,那么$(x,y,z)$就是一个三元环
6. 将$vis$数组清空
7. 继续枚举,直到整张图的点都枚举过
时间复杂度大约为$O(m \sqrt n)$
关于此题容斥的正确性可以这么证明:
设一个三元组$(x,y,z)$,其中$x \lt y \lt z$且存在$k$对不合法关系
则对答案的贡献为$g(0)-g(1)+g(2)-g(3)=1-k+C_{k}^{2}-[k=3]=[k=0]$

1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef unsigned long long ull; 4 const int N = 2e5 + 10; 5 struct REL { int x, y; } rel[N]; 6 int n, m; 7 ull A, B, C, cnt[4], ans; 8 vector<int> lt[N], gt[N], g[N]; 9 int deg[N], vis[N]; 10 ull sumA[N], sumB[N], sumC[N]; 11 12 ull calc1(int x, int y) { 13 if(x > y) swap(x, y); 14 ull res = 0; 15 if(x > 0) res += sumA[x - 1] + x * (B * x + C * y); 16 if(x + 1 < y) res += (y - x - 1) * (A * x + C * y) + (sumB[y - 1] - sumB[x]); 17 if(y + 1 < n) res += (n - 1 - y) * (A * x + B * y) + (sumC[n - 1] - sumC[y]); 18 return res; 19 } 20 21 ull calc3(int x, int y, int z) { 22 if(x > y) swap(x, y); 23 if(x > z) swap(x, z); 24 if(y > z) swap(y, z); 25 assert(x < y && y < z); 26 ull res = 0; 27 res += A * x + B * y + C * z; 28 return res; 29 } 30 31 void sol() { 32 for(int i = 0 ; i < n ; ++ i) { 33 ull c = C * i * (1ll * i * (i - 1) / 2); 34 ull b = B * i * i * (n - i - 1); 35 ull a = A * i * ((1ll * n - i - 1) * (n - i - 2) / 2); 36 cnt[0] += a + b + c; 37 } 38 for(int i = 1 ; i <= m ; ++ i) { 39 int x = rel[i].x, y = rel[i].y; // x < y 40 gt[x].push_back(y), lt[y].push_back(x); 41 ++ deg[x], ++ deg[y]; 42 cnt[1] += calc1(x, y); 43 } 44 for(int i = 0 ; i < n ; ++ i) { 45 if(lt[i].size()) sort(lt[i].begin(), lt[i].end()); 46 if(gt[i].size()) sort(gt[i].begin(), gt[i].end(), greater<int>()); 47 ull tot = lt[i].size() * gt[i].size(); 48 ull sumlt = 0, sumgt = 0, res = 0; 49 int lttot = 0, gttot = 0; 50 for(int x: lt[i]) { 51 res += sumlt + lttot * B * x + lttot * C * i; 52 sumlt += A * x; 53 ++ lttot; 54 } 55 for(int y: gt[i]) { 56 res += gttot * A * i + gttot * B * y + sumgt; 57 sumgt += C * y; 58 ++ gttot; 59 } 60 if(lt[i].size() && gt[i].size()) { 61 res += sumlt * gt[i].size(); 62 res += B * i * tot; 63 res += sumgt * lt[i].size(); 64 } 65 cnt[2] += res; 66 } 67 for(int i = 1 ; i <= m ; ++ i) { 68 int x = rel[i].x, y = rel[i].y; 69 if(deg[x] < deg[y]) swap(x, y); 70 if(deg[x] == deg[y] && x > y) swap(x, y); 71 g[x].push_back(y); 72 } 73 for(int x = 0 ; x < n ; ++ x) { 74 if(g[x].size()) sort(g[x].begin(), g[x].end()); 75 for(int y: g[x]) vis[y] = 1 + x; 76 for(int y: g[x]) 77 for(int z: g[y]) 78 if(vis[z] == 1 + x) 79 cnt[3] += calc3(x, y, z); 80 } 81 ans = cnt[0] - cnt[1] + cnt[2] - cnt[3]; 82 } 83 84 int main() { 85 ios :: sync_with_stdio(0), cin.tie(0), cout.tie(0); 86 freopen("girls.in", "r", stdin); 87 freopen("girls.out", "w", stdout); 88 cin >> n >> m; 89 cin >> A >> B >> C; 90 for(int i = 0 ; i < n ; ++ i) { 91 if(i) sumA[i] += sumA[i - 1], sumB[i] += sumB[i - 1], sumC[i] += sumC[i - 1]; 92 sumA[i] += A * i; 93 sumB[i] += B * i; 94 sumC[i] += C * i; 95 } 96 vector<pair<int, int> > tmp; 97 for(int i = 1 ; i <= m ; ++ i) { 98 cin >> rel[i].x >> rel[i].y; 99 assert(rel[i].x != rel[i].y); 100 tmp.push_back(make_pair(min(rel[i].x, rel[i].y), max(rel[i].x, rel[i].y))); 101 } 102 sort(tmp.begin(), tmp.end()); 103 tmp.erase(unique(tmp.begin(), tmp.end()), tmp.end()); 104 m = tmp.size(); 105 for(int i = 1 ; i <= m ; ++ i) rel[i].x = tmp[i - 1].first, rel[i].y = tmp[i - 1].second; 106 sol(); 107 cout << ans << endl; 108 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号