AtCoderGrandContest015C Nuske vs Phantom Thnook

C - Nuske vs Phantom Thnook

---

Time limit : 4sec / Memory limit : 256MB

Score : 700 points

Problem Statement

Nuske has a grid with N rows and M columns of squares. The rows are numbered 1 through N from top to bottom, and the columns are numbered 1 through Mfrom left to right. Each square in the grid is painted in either blue or white. If Si,j is 1, the square at the i-th row and j-th column is blue; if Si,j is 0, the square is white. For every pair of two blue square a and b, there is at most one path that starts from a, repeatedly proceeds to an adjacent (side by side) blue square and finally reaches b, without traversing the same square more than once.

Phantom Thnook, Nuske's eternal rival, gives Q queries to Nuske. The i-th query consists of four integers xi,1, yi,1, xi,2 and yi,2 and asks him the following: when the rectangular region of the grid bounded by (and including) the xi,1-th row, xi,2-th row, yi,1-th column and yi,2-th column is cut out, how many connected components consisting of blue squares there are in the region?

Process all the queries.

Constraints

• 1≤N,M≤2000
• 1≤Q≤200000
• Si,j is either 0 or 1.
• Si,j satisfies the condition explained in the statement.
• 1≤xi,1≤xi,2≤N(1≤i≤Q)
• 1≤yi,1≤yi,2≤M(1≤i≤Q)

---

Input

The input is given from Standard Input in the following format:

N M Q
S1,1..S1,M
:
SN,1..SN,M
x1,1 yi,1 xi,2 yi,2
:
xQ,1 yQ,1 xQ,2 yQ,2

Output

For each query, print the number of the connected components consisting of blue squares in the region.

---

Sample Input 1

Copy

3 4 4
1101
0110
1101
1 1 3 4
1 1 3 1
2 2 3 4
1 2 2 4

Sample Output 1

Copy

3
2
2
2

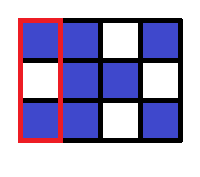
In the first query, the whole grid is specified. There are three components consisting of blue squares, and thus 3 should be printed.

In the second query, the region within the red frame is specified. There are two components consisting of blue squares, and thus 2 should be printed. Note that squares that belong to the same component in the original grid may belong to different components.

---

Sample Input 2

Copy

5 5 6
11010
01110
10101
11101
01010
1 1 5 5
1 2 4 5
2 3 3 4
3 3 3 3
3 1 3 5
1 1 3 4

Sample Output 2

Copy

3
2
1
1
3
2

// 二维前缀和 图的性质 连通块

/*
  对于不包含环的图,连通块数目=点数-边数（这是什么鬼。。。）
 */

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cstdlib>

using namespace std;

const int N = 2010;

char mp[N][N];

int n, m, q, a[N][N], c[N][N], b[N][N];

#define plus(arr, val, i, j) arr[i][j] = arr[i][j - 1] + arr[i - 1][j] - arr[i - 1][j - 1] + (val)

int main() {
    scanf("%d%d%d", &n, &m, &q);
    for(int i = 1 ; i <= n ; ++ i) {
        scanf("%s", mp[i] + 1);
    }

    for(int i = 1 ; i <= n ; ++ i) {
        for(int j = 1 ; j <= m ; ++ j) {
            plus(a, mp[i][j] == '1', i, j);
            plus(b, mp[i][j] == '1' && mp[i][j - 1] == '1', i, j);
            plus(c, mp[i][j] == '1' && mp[i - 1][j] == '1', j, i);
        }
    }

    for(int i = 1, x, y, xx, yy ; i <= q ; ++ i) {
        scanf("%d%d%d%d", &x, &y, &xx, &yy);
        printf("%d\n",
               (a[xx][yy] - a[x - 1][yy] - a[xx][y - 1] + a[x - 1][y - 1]) -
               (b[xx][yy] - b[xx][y] - b[x - 1][yy] + b[x - 1][y]) -
               (c[yy][xx] - c[yy][x] - c[y - 1][xx] + c[y - 1][x]));
    }
}