codeforces863E Turn Off The TV

E. Turn Off The TV

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Luba needs your help again! Luba has n TV sets. She knows that i-th TV set will be working from moment of time li till moment ri, inclusive.

Luba wants to switch off one of TV sets in order to free the socket. Let's call some TV set redundant if after switching it off the number of integer moments of time when at least one of TV sets is working won't decrease. Luba will be very upset if she has to switch off a non-redundant TV set.

Help Luba by telling her the index of some redundant TV set. If there is no any, print -1.

Input

The first line contains one integer number n (1 ≤ n ≤ 2·105) — the number of TV sets.

Then n lines follow, each of them containing two integer numbers li, ri (0 ≤ li ≤ ri ≤ 109) denoting the working time of i-th TV set.

Output

If there is no any redundant TV set, print -1. Otherwise print the index of any redundant TV set (TV sets are indexed from 1 to n).

If there are multiple answers, print any of them.

Examples

input

3
1 3
4 6
1 7

output

1

input

2
0 10
0 10

output

1

input

3
1 2
3 4
6 8

output

-1

input

3
1 2
2 3
3 4

output

2

Note

Consider the first sample. Initially all integer moments of time such that at least one TV set is working are from the segment [1;7]. It's easy to see that this segment won't change if we switch off the first TV set (or the second one).

Note that in the fourth sample you can switch off the second TV set, since even without it all integer moments such that any of the TV sets is working denote the segment [1;4].

题目大意（如果没有理解错的话）：

你有若干台电视机，其中第i台电视机在[li, ri]时间播放
你需要找到一台电视机，使得删去这台电视机之后原先的所有可以播放电视的时间段上仍有电视机播放
如果找不到，输出-1

 

思路：

首先离散化一下，然后对于每个电视机的时间段用差分的思路进行区间增加，然后再定义前缀数组表示1~i中被多个电视机播放的时间点的个数，查询的时候直接提取这一段区间然后看是否为0即可。

（然而离散化的时候需要把l[i]-1也加进去）

考虑如下数据：

3

1 2

4 5

2 4

正确答案应该输出-1，而如果去掉了l[i]-1就离散化的话输出3

因为错误程序会把4转换成了3，然后就成了[1,2][3,4][2,3]了，然而第三个电视机是不能删掉的，不然时间3没有电视机播放

 

官方题解：

Firstly let's compress the moments of time. Note that storing only l and r isn't enough (consider pairs ([1, 2], [3, 4]) and ([1, 2], [4, 5])), you also should take (l - 1).

Now moments of time are up to 6·105. For every moment calculate the number of segments to cover it (make cntl +  = 1 and cntr + 1 -  = 1 for each segment and take prefix sums over this array). Then let prefi be the number of moments of time covered by only one segment on some prefix up to i-th moment.

And finally if for some segment [l, r] from the input prefr - prefl - 1 is 0 then you can safely delete this segment.

Overall complexity: .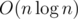

 

 

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cstdlib>

using namespace std;

const int N = (2e5 + 10) * 3;

int n, l[N], r[N], num[N], size, val[N], cnt[N];

int main() {
    scanf("%d", &n);
    for(int i = 1 ; i <= n ; i ++) {
        scanf("%d%d", &l[i], &r[i]);
        num[i] = l[i];
        num[i + n] = r[i];
        num[i + n + n] = l[i] - 1;
    }
    sort(num + 1, num + 1 + n * 3);
    size = unique(num + 1, num + 1 + n * 3) - num - 1;
    for(int i = 1 ; i <= n ; i ++) {
        l[i] = lower_bound(num + 1, num + 1 + size, l[i]) - num;
        r[i] = lower_bound(num + 1, num + 1 + size, r[i]) - num;
        val[l[i]] ++;
        val[r[i] + 1] --;
    }
    for(int i = 1 ; i <= size ; i ++) {
        val[i] += val[i - 1];
    }
    for(int i = 1 ; i <= size ; i ++) {
        cnt[i] += cnt[i - 1] + (val[i] == 1);
    }
    for(int i = 1 ; i <= n ; i ++) {
        if(cnt[r[i]] - cnt[l[i] - 1] == 0) {
            printf("%d\n", i);
            return 0;
        }
    }
    puts("-1");
}