Luogu 2473 奖励关

题目描述

你正在玩你最喜欢的电子游戏，并且刚刚进入一个奖励关。在这个奖励关里，系统将依次随机抛出k次宝物，每次你都可以选择吃或者不吃（必须在抛出下一个宝物之前做出选择，且现在决定不吃的宝物以后也不能再吃）。

宝物一共有n种，系统每次抛出这n种宝物的概率都相同且相互独立。也就是说，即使前k-1 次系统都抛出宝物1（这种情况是有可能出现的，尽管概率非常小），第k次抛出各个宝物的概率依然均为1/n。

获取第 i 种宝物将得到Pi分，但并不是每种宝物都是可以随意获取的。第i种宝物有一个前提宝物集合Si。只有当Si中所有宝物都至少吃过一次，才能吃第i 种宝物（如果系统抛出了一个目前不能吃的宝物，相当于白白的损失了一次机会）。注意，Pi 可以是负数，但如果它是很多高分宝物的前提，损失短期利益而吃掉这个负分宝物将获得更大的长期利益。

假设你采取最优策略，平均情况你一共能在奖励关得到多少分值？

输入输出格式

输入格式：

第一行为两个正整数k 和n，即宝物的数量和种类。以下n行分别描述一种

宝物，其中第一个整数代表分值，随后的整数依次代表该宝物的各个前提宝物（各

宝物编号为1到n），以0结尾。

输出格式：

输出一个实数，保留六位小数，即在最优策略下平均情况的得分。

输入输出样例

输入样例#1：

1 2
1 0
2 0

输出样例#1：

1.500000

输入样例#2：

6 6
12 2 3 4 5 0
15 5 0
-2 2 4 5 0
-11 2 5 0
5 0
1 2 4 5 0

输出样例#2：

10.023470

说明

1 <= k <= 100, 1 <= n <= 15，分值为[-106,106]内的整数。

设f[i][S]为第i轮决策，当前已经吃了集合S的物品（可以重复，因为吃某个物品的前提条件与数量无关，仅与吃过的物品有关）。

根据期望公式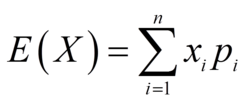以及对于每一个可能出现的物品都有吃（如果可以吃的话）或者不吃的选择，而且每种物品出现的概率均为1/n。

那么可以得到 E(i,S) = sum{1/n * max(E(i + 1, S), ((S & pre[a]) == pre[a]) * E(i + 1, S | (1 << (a - 1)))}，其中a是枚举的可能出现的物品，pre是某种物品如果能吃到的最小前置物品满足集合。

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cstdlib>

using namespace std;

int k, n, pre[20], val[20];
double f[200][1 << 17];

int main() {
    // freopen("in", "r", stdin);
    scanf("%d%d", &k, &n);
    for(int i = 1, t ; i <= n ; i ++) {
        scanf("%d", &t);
        val[i] = t;
        while(scanf("%d", &t) == 1 && t)
            pre[i] |= 1 << (t - 1);
    }
    for(int T = k ; T >= 1 ; T --) {
        for(int j = 0 ; j < (1 << n) ; j ++) {
            for(int i = 1 ; i <= n ; i ++) {
                if((j & pre[i]) == pre[i])
                    f[T][j] += max(f[T + 1][j], f[T + 1][j | (1 << (i - 1))] + val[i]);
                else 
                    f[T][j] += f[T + 1][j];
            }
            f[T][j] /= n;
        }
    }
    printf("%.6lf\n", f[1][0]);
}