24.11.21
A
怎么只有我一个写这种唐诗做法啊/kk
当括号匹配时会对若干区间造成贡献。
如果我们考虑每个右括号作为右端点统计贡献区间的话,左侧所有和它同一括号范围内(或最外层)的同层的左括号作为左端点和其构成一个贡献区间。
举例子来说
\(({\color{blue}(}))({\color{yellow}(}){\color{yellow}(}{\color{red})})\)
在上串中,在统计 \(\color{red})\) 作为右端点的区间时,那两个 \(\color{yellow}(\) 均与其构成贡献区间。
注意标蓝的左括号虽然与其层数相同,但是和它分别处于两个外层括号包裹下,已经隔了一层可悲的厚屏障了(雾不与其构成贡献区间。对于左括号同理。
所以我们倒着扫一遍,对于每个左括号求出它右侧有多少右括号与其构成贡献区间,在差分数组上这一位就加上多少。
顺着扫一遍,对于每个右括号求出它左侧有多少左括号与其构成贡献区间,在差分数组上下一位减去多少。如果我们记
(为 \(1\),)为 \(-1\)。
那么我们知道对于前缀和为 \(x\) 处的右括号与之匹配的左括号处的前缀和应为 \(x + 1\)。
如果出现了右括号,其包裹的区间内的左括号不会再做贡献,所以将其包裹的区间里的左括号(前缀和为应为 \(x + 2\))的计数器清零。对于左括号同理。与其匹配的右括号为 \(x - 1\),出现左括号时将 \(x\) 的计数器清零。
或者我们考虑另一种做法。
考虑每对匹配括号对其区间内的贡献一对匹配的括号一定会对其区间内造成贡献。
此外如果左右有与其同层的配对括号那么与其拼接同样是合法的,
如果左侧的同层括号对数是 \(L\),右侧的是 \(R\),那么该括号对区间的贡献为 \((L + 1)\cdot(R + 1)\)。
std 写的是第二种。
没有用差分区间加,子区间直接继承父区间的答案,再算自己新的贡献,这就是两侧匹配括号的答案,而再往里的子区间会继承它的答案计算答案。
麻了 A 这么唐一个题让我写题解怎么比 CD 题解加起来还长。写题唐写题解也唐是吧。
B
原到了 8.30 号。
何日重到苏澜桥-数论版。
理解一下 \(\gcd \neq 1\) 的情况,就是每乘一个 \(10\) 之后 \(D\) 就消去一个 \(2 > \times 5\)。然后 \(2^{20} > D\),就可以消去 \(2, 5\) 的影响。
PC 题解
设 \(h_i\) 表示 \(1\sim i\) 字符构成的十进制数字,即 \(h_i=\sum\limits_{j=1}^{i}s_i10^{i-j}\) 。
一个子串 \([l,r]\) 构成的十进制数字能整除 \(D\) 当且仅当 \(h_r-h_{l-1}\times10^{r-l+1}\equiv0\pmod D\) ,也就是说 \(h_r\equiv h_{l-1}\times10^{r-l+1}\pmod D\)。
设 \(f_i\) 为以 \(i\) 为结尾子串不能被 \(D\) 整除的前 \(i\) 个字符的划分方案数,\(g_i\) 为以 \(i\) 为结尾子串能被 \(D\) 整除的前 \(i\) 个字符的划分方案数,
每次转移 \(f_i=\sum\limits_{h_i-h_{j-1}\times10^{i-j+1}\not\equiv0\pmod D}g_j\),\(g_i=\sum\limits_{h_r-h_{l-1}\times10^{r-l+1}\equiv0\pmod D}f_j+g_j\)。
暴力向前扫是 \(O(n^2)\) 的,考虑优化。
若 \(\gcd(10,D)=1\),那么上述同余方程可以写成 \(h_r\times10^{-r}\equiv h_{l-1}\times10^{-(l-1)}\pmod D\),将 \(f_i,g_i\) 放进 \(h_i\times10^{-i}\) 对应桶里,每次查询桶里数的和即可。
若 \(\gcd(10,D)\neq1\),这时候 \(10\) 在\(\mod D\) 意义下没有逆元,不能用上述方法。
将 \(D\) 分解为 \(2^x5^yz\) 的形式。
那么同余方程可以分解为两个:
\(\begin{cases}h_r\equiv h_{l-1}\times10^{r-l+1}\pmod {2^x5^y}\\h_r\equiv h_{l-1}\times10^{r-l+1}\pmod {z}\end{cases}\)
如果要满足 \([l,r]\) 构成的十进制数字能整除 \(D\),必须同时满足上方两个式子。
由于 \(D\) 最大是 \(10^6\),也就是说 \(\max(x,y)\le20\),所以 \(r-l+1\ge20\) 的时候,\(h_{l-1}\times10^{r-l+1}\equiv0\pmod {2^x5^y}\)。
此时需要判断的条件就变成了:
\(\begin{cases}h_r\equiv 0\pmod {2^x5^y}\\h_r\equiv h_{l-1}\times10^{r-l+1}\pmod {z}\end{cases}\)
而 \(\gcd(10,z)=1\) ,套用 \(\gcd(10,D)=1\) 的方法就行了。
而当 \(r-l+1 < 20\) 的时候不能这么做,这部分暴力向前扫 \(20\) 个就行了。
C
yyzz 题解
首先我们不考虑 “两个矩阵如果删除的元素位置不同,但最后得到的结果相同,我们认为是相同的” 这句话,可以得到一个朴素的 dp:\(f_{i,j}=\sum\limits_{j-k\leq l \leq j+k}f_{i-1,l}\),然后这个用前缀和优化转移即可做到 \(\mathcal O(nm)\)。
回过头来观察这句话对结果的影响,同一行一段相等的元素,移除它们的结果是一样的,这意味着我们会计算许多重复状态,考虑去除重复贡献。
我们发现对于第 \(i\) 行相邻的两个相同元素 \(j-1,j\),它们对应上一层的范围是这样的:
(红线为 \(j-1\),蓝线为 \(j\))
显然,上图中被白线框出来的线段被重复覆盖了,这一段为 \([j-k,j+k-1]\)。
我们新增一个数组 \(g\) 来记录每个元素可能会重复计算的贡献,那么 \(f\) 的转移方程就不难推出:
\[f_{i,j}=\sum\limits_{j-k\leq l \leq j+k}f_{i-1,l}-\sum\limits_{j-k+1\leq l \leq j+k}g_{i-1,l} \]注意 \(g\) 的起始位置为 \(j-k+1\),因为左端点不会产生重复贡献。
根据 \(g\) 数组的定义和我们上面推出的式子,可以得到转移:
\[g_{i,j}=[a_{i,j}=a_{i,j-1}]\times (\sum\limits_{j-k\leq l\leq j+k-1}f_{i-1,l}-\sum\limits_{j-k+1\leq l\leq j+k-1}g_{i-1,l}) \]答案即为 \(\sum\limits_{1\leq i\leq m} f_{n,i}-\sum\limits_{2\leq i\leq m} g_{n,i}\)。
然后这个也是从一段区间转移,前缀和优化即可,时间复杂度 \(\mathcal O(nm)\)。
D
NT 题解
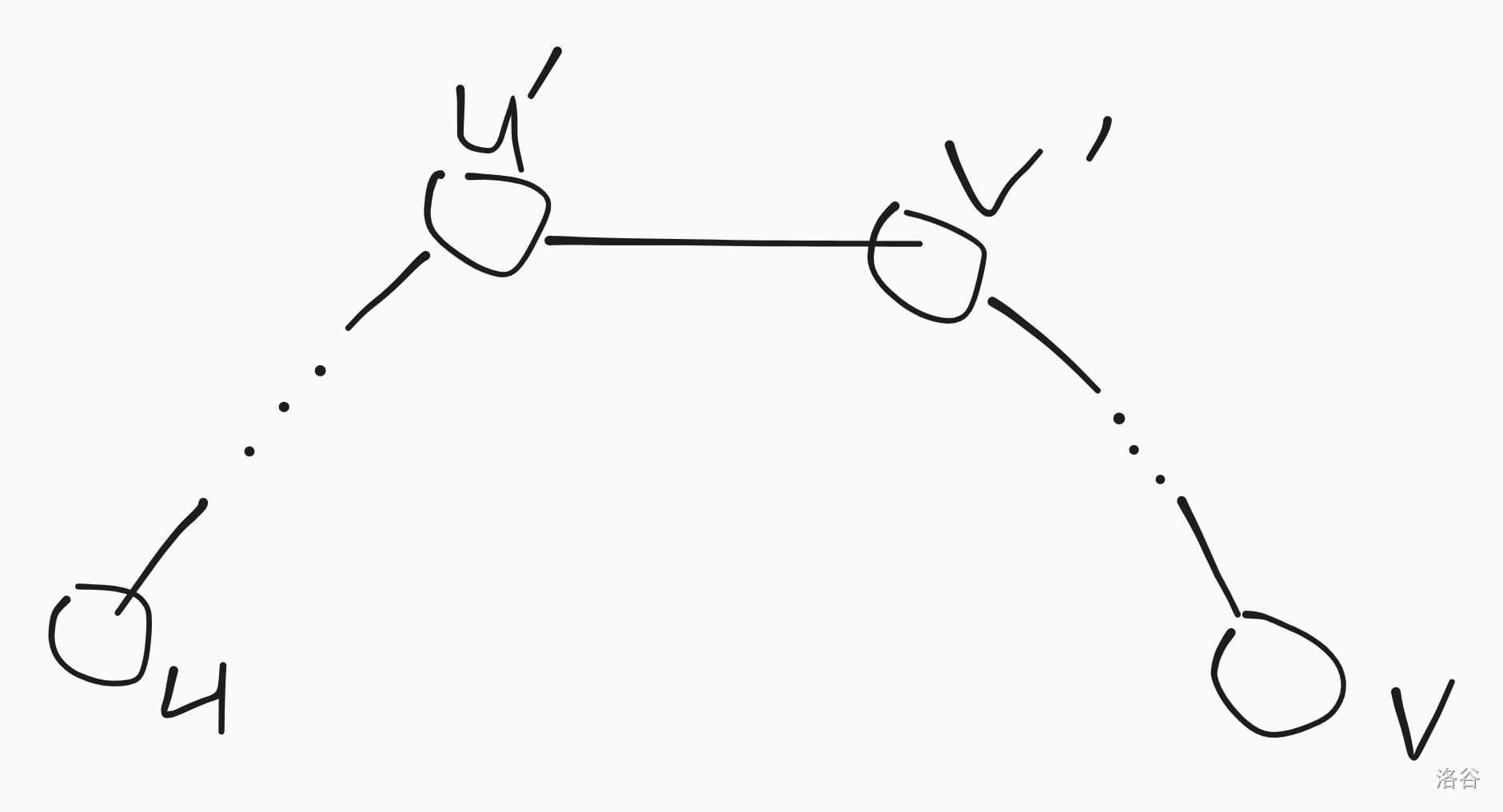
首先对于询问我们可以发现最后的答案一定是形如下图:
并且最大的边一定在左右两侧中的一侧。
那我们考虑 kruskal 从小到大加边,每次去合并连通块,因为我们是从小到大加的,所以最后答案一定会变成下图:
那么我们考虑合并的时候将出边和询问都合并到一个点上,使用启发式合并可以做到 \(O(n\log^2 n)\)。
不是您搁这打 CodeGolf 呐?
把询问存到点上(存对应另一个点和编号)。
思路是这么个思路,里面计算答案和合并的过程感觉不如换张图理解:
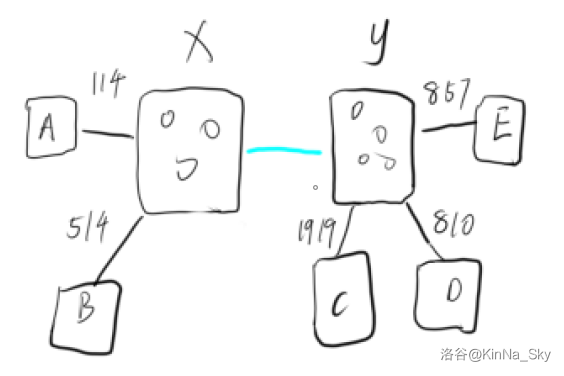
启发式合并中,不妨使 \(x\) 为边数和询问数较少的集合。
如果我们现在最小边是蓝边,我们要计算以其作为答案即次大边的询问。
它已经是当前最小边了,要计算以其为次大边作为答案我们就要走且仅走一条其他边,由于 \(x\) 边数和询问数更少,所以
- 扫 \(x\) 非 \(y\) 的出点,查 \(y\) 中是否有询问这个出点的,回答那些询问;
- 扫 \(x\) 的询问,查 \(y\) 是否有这个询问的出点,回答那些询问。
合并就是合并。把边和未回答的询问放到一个点上,由于 \(x\) 较少,所以把 \(x\) 的边和询问插到 \(y\) 里。

注意也要更改别的集合的出边和询问,让原来指向 \(x\) 的边和询问指向 \(y\)。