AT_abc379_g
过于一眼的轮廓线 dp。
兼纪念 abc 首场无伤 AK。

首先我们可以经过缜密的计算的得到矩形的宽不超过 \(14\)。
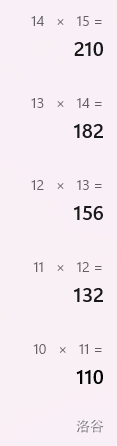
然后现在你有 \(4\) 个数(边界视作 \(0\))。
不难想到 \(4\) 进制状压轮廓线 dp。
轮廓线 dp
状压 dp 的一种,轮廓线是分隔已处理部分与未处理部分的线。
在本题中,轮廓线应形如这样:
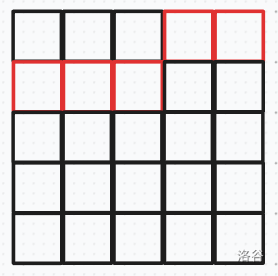
将轮廓线上的点从左到右压在二进制位从低到高位上。
转移时枚举交界(那个黑色的拐点)的状态判断转移的合法性进行转移。
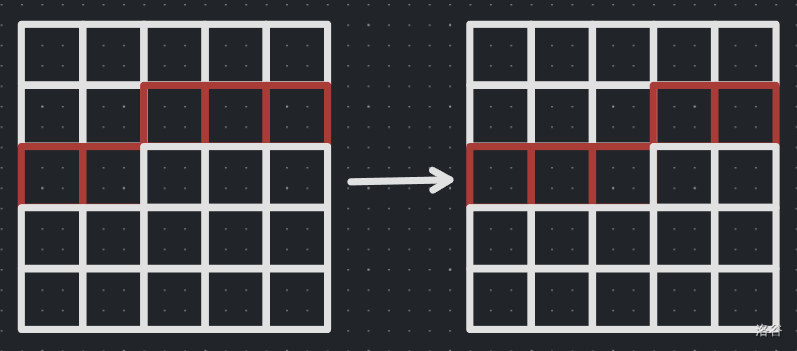
由于显然有很多无用状态直接用 map 存 dp 状态和值。
那么在 \((i, j)\) 格子处我们要考虑上面和左面(若 \(j = 1\) 则不需)的格子判断转移是否合法。
提取上面的值:up = (sta >> ((j - 1) * 2)) & 3;。
提取左面的值:lf = (sta >> ((j - 2) * 2)) & 3;。
枚举填什么数(\(k\)),注意还有题目要求的限制。
即 mp[i][j] == '?' || mp[i][j] == '0' + k。
在转移合法情况下,我们从当前状态 \(sta\) 得到下一个状态 \(nxt\)。
提取出无关状态,然后把我们枚举的数塞进去:
int Base = (1 << m) - 1;
// ...
int tmp = Base ^ (3 << ((j - 1) * 2));
int nxt = (sta & tmp) | (k << ((j - 1) * 2));
然后计数 dp 正常转移,由于转移只与上一轮廓线有关可以滚动数组。



