第四章----关系代数运算

一、关系代数运算

（一）关系代数运算的特点

1、抽象的关系操作语言

2、运算对象和运算结果都是关系

（二）关系代数运算符

　　

 

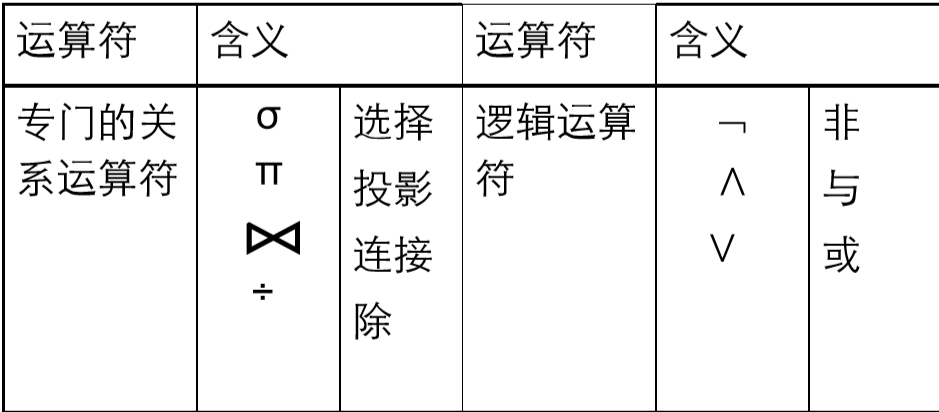
（三）关系代数运算

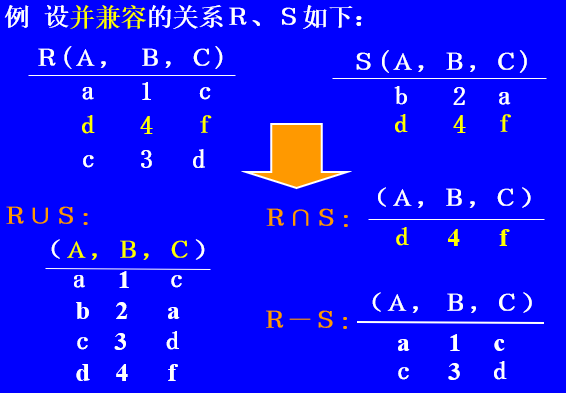
传统的集合运算：

a）并兼容的关系：

　　若两个关系的属性个数相同，且对应属性的域也相同，则称这两个关系是并兼容的。

b）并运算：记作R∪S  

c）差运算：记作R-S

d）交运算：记作R∩S

b）c）d）中关系R和S必须是并兼容的。

 

 e）笛卡尔积乘积运算

　　两个属性个数分别是m、n，元组个数分别为k₁，k₂的关系R和S，它们的笛卡尔乘积是一个关系，

该关系属性个数为m+n、元组个数为k₁*k₂，记为R×S

 

专门的关系运算：

• 选择
• 投影
• 连接
• 除

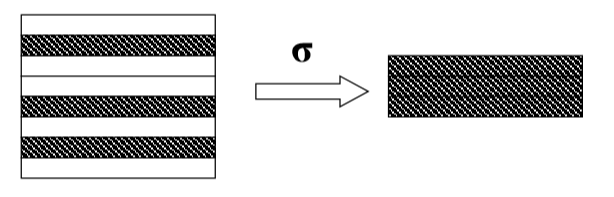
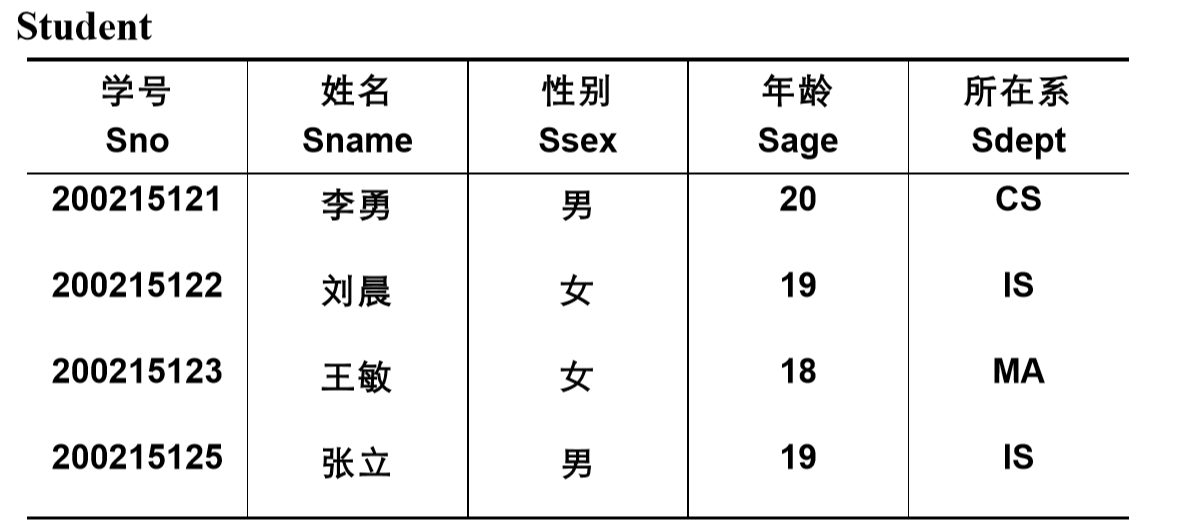
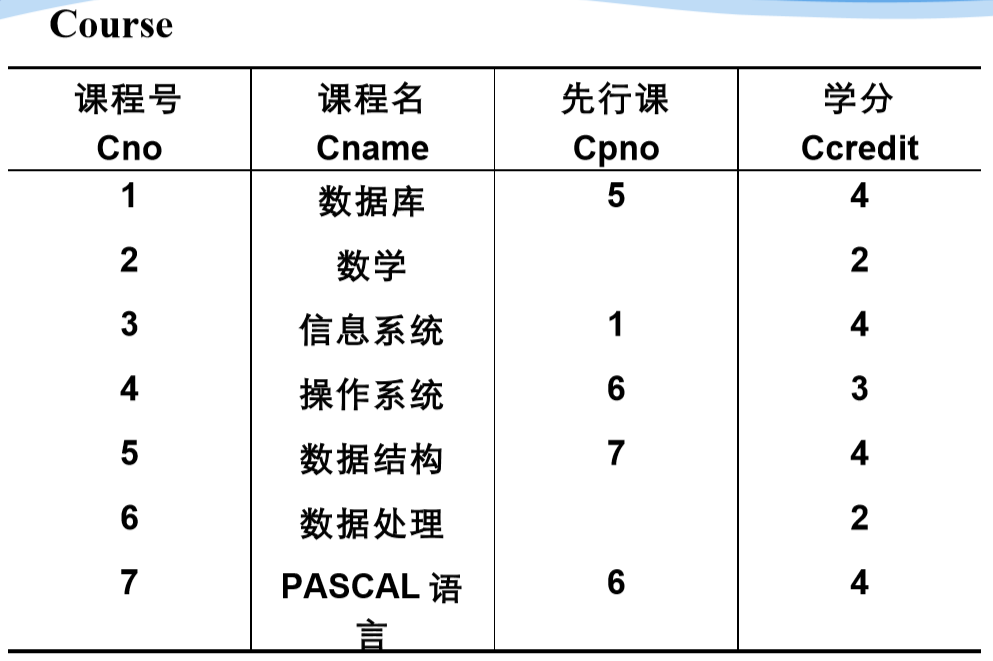
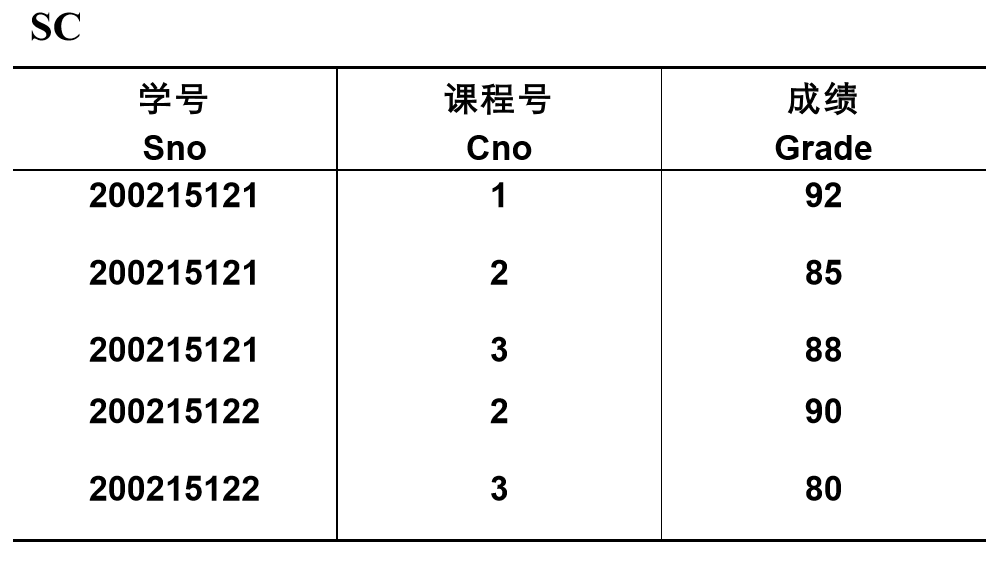
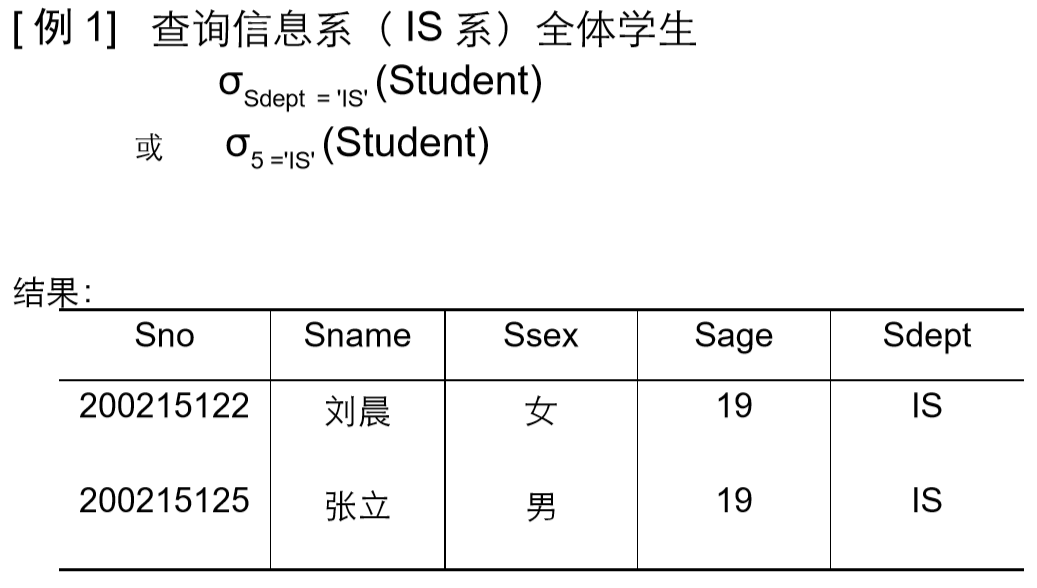
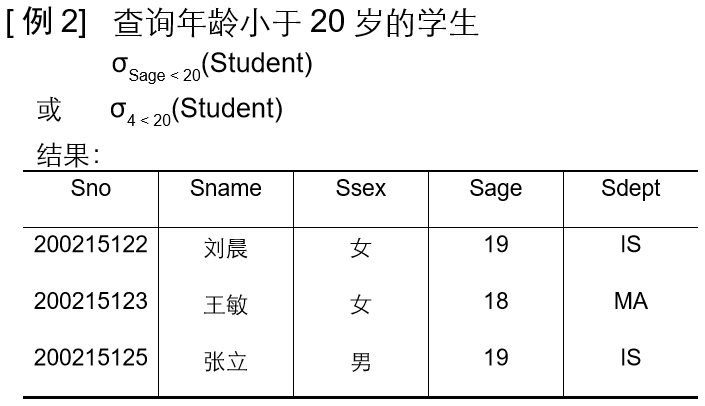
选择

1) 选择又称为限制（Restriction）　　

2) 选择运算符的含义

　　在关系R中选择满足给定条件的诸元组         

　　　　 σF(R) = {t|t∈R∧F(t)= '真'}

　　F：选择条件，是一个逻辑表达式，基本形式 为： X₁θY₁

3）选择运算是从关系R中选取使逻辑表达式F为真的元组，是从行的角度进行的运算

                           

                                                                   

 

 

 投影

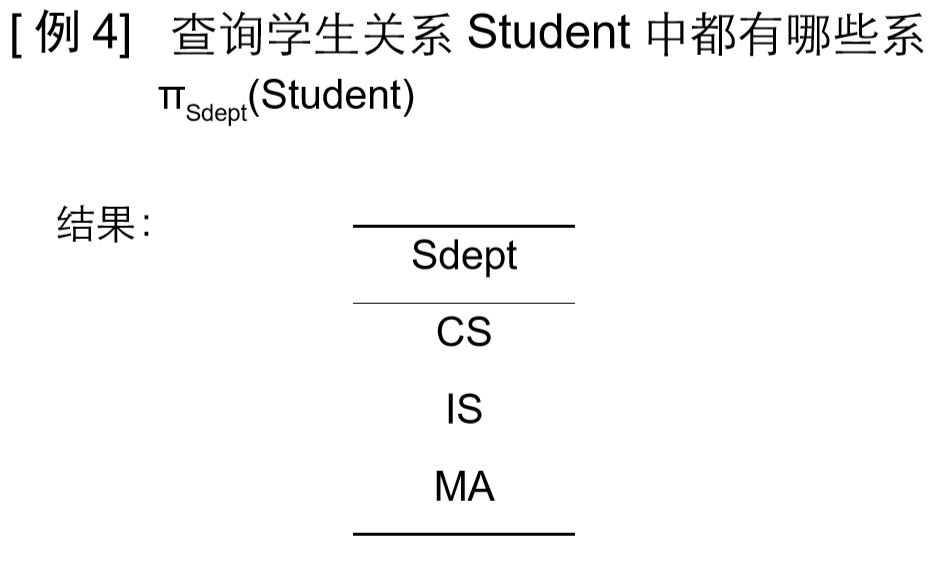
1）投影运算符的含义

从R中选择出若干属性列组成新的关系         

    πA(R) = { t[A] | t R }

　　A ： R中的属性列 

2）投影操作主要是从列的角度进行运算

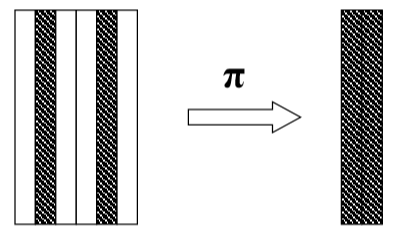
 但投影之后不仅取消了原关系中的某些列，而且还能取消某些元组（避免重复行）

 

               

 

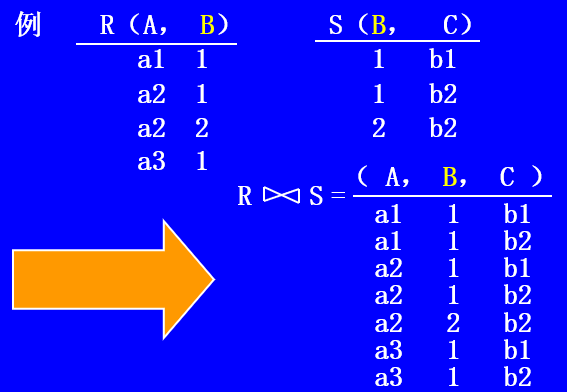
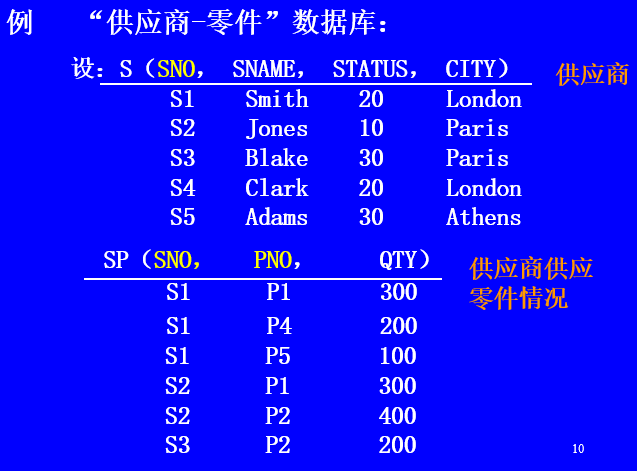
连接 

一般连接，即θ-连接。记为：

                                     

 

 

 自然连接：自然连接是两个关系在同名属性上进行等值连接的运算。

记为：

　　　　

 

      

 

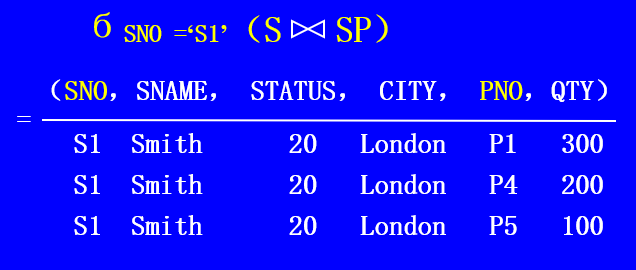
除

我也不是很懂.. 

https://blog.csdn.net/u012411414/article/details/41048861?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task

 

//有补充会添加