实时光线追踪（1）Denoising: Spatio-Temporal Filtering

目录

• Spatial Filtering（空间滤波）
  • 基于距离的高斯滤波
  • Bilateral Filtering（双边滤波）
  • 基本问题
• Temporal Filtering（时序滤波）
  • Motion Vector
  • Velocity Buffer [TODO]
  • 混合系数
  • 基本问题
• SVGF [2017]
  • Joint Bilateral Filtering（联合双边滤波）
  • 加速 Spatial Filtering
    • 可分离的高斯滤波
    • A-trous Wavelet
• A-SVGF [2018]
  • 估计 Temporal Gradient
  • 重建 Temporal Gradient Texture
  • 计算 Temporal 混合系数
• 不同种类信号的 Filtering
  • Shadow Filtering
  • Indirect Diffuse Filtering
  • Indirect Specular/Glossy Filtering
  • Radiance Filtering
• 更可靠的 Motion Vectors [2021]
  • Shadow Motion Vector
  • Glossy Motion Vector
  • Dual Motion Vector
• 基于 BRDF 预积分的信号解调 [2021]
  • BRDF 预积分
  • Lighting Filtering
• 其它 [TODO]
  • Outliers Removal
  • ID Detection
  • Clampping [TODO]
  • 动静像素差异处理 [UFSH2023]
• 参考

denoising 主要分为 先验方法 和 后验方法，所谓后验方法就是指在已经采样完的信号上做降噪，先验方法往往是指如何做更高质量的采样来减少噪声。

Spatial Filtering（空间滤波）

对空间上邻域的 pixels 进行复用（其实就是混合起来），从而增加采样数，让当前图像噪声更加小些。

\[\tilde{C} = \frac{\sum_{k} w_kC_k}{\sum_{k} w_k} \]

\(k\) 为空间邻域 pixels 数（即样本数），\(w\) 为邻域样本的权重，\(C\) 为降噪前的 color，\(\tilde{C}\) 为降噪后的 color。

基于距离的高斯滤波

仅考虑距离因素，会让图像均匀变糊，损失了大量有用的高频信息。

Bilateral Filtering（双边滤波）

额外考虑了颜色因素（基于认为颜色变化剧烈的地方是边界，不应该贡献太多权重）

\[w(i, j, k, l)=\exp \left(-\frac{(i-k)^{2}+(j-l)^{2}}{2 \sigma_{d}^{2}}-\frac{\|I(i, j)-I(k, l)\|^{2}}{2 \sigma_{r}^{2}}\right) \]

\(\sigma_d\) 和 \(\sigma_r\) 都是主观设置的常量，即自己来决定各因素的权重影响。

基本问题

• 带宽开销与降噪质量的权衡：空间上可复用的邻域 pixels 实际上是很多很多的，但是都读取它们的信息将导致巨量带宽开销，因此往往只能取最高质量的若干个邻域 pixels 来复用。当然，怎么衡量质量也是另一个问题。
• 过度模糊：spatial filtering 实际上就相当于一个空间上的图像模糊操作，并且很容易产生过度模糊丢失高频信息（细节）的图像。

Temporal Filtering（时序滤波）

对时序上的 pixels 进行复用，理论上其实历史帧图像中的所有 pixels 都可以被用来尝试复用，但由于性能成本问题，我们一般只会找最高质量的那个历史 pixel，也就是想找到本帧某 pixel 对应上一帧哪个 pixel 然后进行线性混合。

当然，我们不能简单地去找相同的屏幕 uv 坐标上的 pixel 来混合；因为物体和摄像机随时都会发生移动等变化，这时候就需要借助 motion vector 来找到上帧对应的准确屏幕位置。

Motion Vector

back projection（后向投影）：用于计算出 pixel 在两帧之间的 motion vector（即要找到本帧某 pixel 对应上一帧哪个 pixel）。

仅考虑镜头变化的情况：

float3 HistoryScreenPosition = float3(ScreenPosition, DeviceZ);
float4 ThisClip = float4(HistoryScreenPosition, 1);
float4 WorldPosition = mul(ThisClip, ClipToWorld); // 乘上当前帧的逆视口变换
float4 PrevClip = mul(WorldPosition, WorldToPrevClip); // 乘上历史帧的视口变换
float3 PrevScreenPosition = PrevClip.xyz / PrevClip.w; // 得到历史帧对应屏幕位置
float2 MotionVector = PrevScreenPosition - ScreenPosition;

然而，实际上场景中的物体也可能会发生变化，仅考虑镜头变化（视口变换）可能会得到坏的 pixel 样本，因此更准确的 motion vector 应当考虑上物体变化：

float3 HistoryScreenPosition = float3(ScreenPosition, DeviceZ);
uint TransformID = GetTransformIDFromScreen(HistoryScreenPosition); // 从屏幕信息（一般是GBuffer或VBuffer）中获取 transform ID，可以理解为当前物体（mesh instance）的 ID
float4 ThisClip = float4(HistoryScreenPosition, 1);
float4 WorldPosition = mul(ThisClip, ClipToWorld); // 乘上当前帧的逆视口变换
float4 LocalPosition = mul(WorldPosition, Transforms[TransformID].WorldToLocal); // 乘上所在物体的当前帧的逆世界变换，得到相对于物体的局部位置
float4 PrevWorldPosition = mul(LocalPosition, Transforms[TransformID].LocalToPrevWorld); // 乘上所在物体的历史帧的世界变换，得到历史帧的世界位置
float4 PrevClip = mul(PrevWorldPosition, WorldToPrevClip); // 乘上历史帧的视口变换
float3 PrevScreenPosition = PrevClip.xyz / PrevClip.w; // 得到历史帧对应屏幕位置
float2 MotionVector = PrevScreenPosition - ScreenPosition;

Velocity Buffer [TODO]

混合系数

假设我们已经有了 motion vector，那么只需要对本帧 pixel 的位置施加这个 motion vector 来得到上帧对应 pixel 的屏幕位置，并且这个历史屏幕位置没有超出历史帧屏幕范围，那么就可以将上一帧对应位置的 pixel 的 color 与本帧 pixel 的 color 进行线性混合：

\[\bar{C}^{(i)}=\operatorname{Filter}\left[\tilde{C}^{(i)}\right] \]

\[\bar{C}^{(i)}=\alpha \bar{C}^{(i)}+(1-\alpha) C^{(i-1)}​ \]

~ 为未空间滤波，- 为已空间滤波；\(\alpha\) 一般为 0.1~0.2

基本问题

• 图像滞后，鬼影问题（ghosting）：由于 temporal filtering 实际就是混合历史帧的 color，因此图像的更新是会引入延迟的，尤其是当场景物体快速运动时，往往会造成残影拖尾的效果，非常影响观感。
• 屏幕空间信息不足：比如，历史帧屏幕外的点进入了当前帧屏幕内；再比如，被遮挡的物体突然在下一帧的屏幕出现。

SVGF [2017]

SVGF（Spatio-Temporal Variance Guided Filter）主要是采用了更聪明也更符合现代 G-Buffer 管线的 spatial filtering 方法，再搭配上 temporal filtering，可以说是 real-time denoising 的里程碑。

SVGF = Joint Bilateral Filtering + Temporal Filtering。SVGF 算是 real-time denoising 的经典方案了，后续的降噪方案大都基于此去改进或创新。

Joint Bilateral Filtering（联合双边滤波）

Joint Bilateral filtering：一种 spatial filtering 方法，通过充分利用 G-buffer 的各种属性作为参考，来控制滤波的核和权重。实际关键就是在判断高频信息属于噪声还是图像信息，而 G-buffer 是光栅化过程生成的完全没有噪声，因此作为滤波的指导是非常有用的。

考虑的点有：

• 联合考虑深度差异和法线（不能简单的单纯考虑深度差异）
  • 实际上就是考虑沿平面的深度差距

\[w_{z}=\exp \left(-\frac{|z(p)-z(q)|}{\sigma_{z}|\nabla z(p) \cdot(p-q)|+\epsilon}\right) \]

• 法线的差异
  • 求出来的值有可能是负值，因此使用了 max() 函数
  • \(\sigma_n\) 是为了更突出法线变化

\[w_{n}=\max (0, n(p) \cdot n(q))^{\sigma_{n}} \]

注：如果使用法线贴图，使用法线贴图变换前的法线。

• 亮度的差异（两点颜色间的灰度差距）：差异过大则认为两点位置靠近边界，贡献不应过大
  • 由于噪声可能会出现干扰，因此需要 variance 指导

\[w_{l}=\exp \left(-\frac{\left|l_{i}(p)-l_{i}(q)\right|}{\sigma_{l} \sqrt{g_{3 \times 3}\left(\operatorname{Var}\left(l_{i}(p)\right)\right)}+\epsilon}\right) \]

方差 Var 的计算：

1. 计算需要滤波的点 7×7 范围内的方差
2. 按时域的方法，通过motion vector计算上一帧对应像素的方差，并计算平均（相当于按时域滤波了，将方差变得时域上平滑）
3. 再在周围 3×3 的区域内做空间的平均滤波

最后某个邻域 pixel 的综合权重就可以计算为

\[w=w_z*w_n*w_l \]

加速 Spatial Filtering

空间滤波核越大，其可得到的邻域信息也越多（样本数也会越多），但性能开销也会越大，而以下方法主要是为了加速大核滤波。

可分离的高斯滤波

如果滤波核采用高斯函数的形式，得益于 2D 高斯可分离成水平垂直两次 1D 高斯滤波的特性，可以对图像进行一个水平方向的 1D 高斯滤波 pass 和一个垂直方向的 1D 高斯滤波 pass，将时间复杂度从 \(O(mnk^2)\) 降到 \(O(2mnk)\)

\(m,n\) 代表图像长宽，\(k\) 代表方形滤波核边长

\[G_{2 D}(x, y)=G_{1 D}(x) \cdot G_{1 D}(y)$​ \]

\[\iint F\left(x_{0}, y_{0}\right) G_{2 D}\left(x_{0}-x, y_{0}-y\right) \mathrm{d} x \mathrm{~d} y=\int\left(\int F\left(x_{0}, y_{0}\right) G_{1 D}\left(x_{0}-x\right) \mathrm{d} x\right) G_{1 D}\left(y_{0}-y\right) \mathrm{d} y \]

A-trous Wavelet

而对于非高斯函数形式或者说更复杂的滤波核（例如联合双边滤波核），就很难像单纯的高斯核那样可分离成两个 1D Pass。这时候就可能需要 a-trous wavelet 方法来优化较大滤波范围的原始2D滤波

a-trous Wavelet：采用多 pass 的方式，每个 pass 使用 3×3 或 5×5 的小滤波范围但逐渐增加采样间隔。

具体来说，第 \(i\) 个 pass 的采样间隔将为 \(2^{i-1}-1\)（相邻两个 pass 的采样间隔相差 \(2^i\)）

ps：其实可以理解成层次化空间滤波。

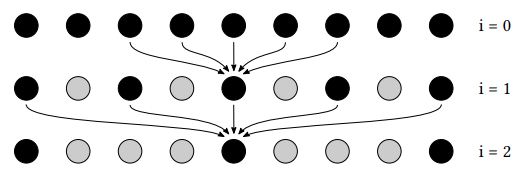
时间复杂度 \(O(mnk^2)\) 降到 \(O(mn\cdot 5^2\cdot log_2{k})\)，只是需要额外的纹理用来写入前一个 pass 的输出（中间结果）。因此对于超大范围的滤波，使用 a-trous wavelet 方法增加的写入开销还是远远比节省的采样开销小。

例如：本来一个 64×64 的 2D 滤波，在该方法中就会变成使用 5 个 Pass，每个 Pass 做 5×5 的 2D 滤波。因为在使用第五个 pass 时，采样间隔为 15，也就是说采样总跨度为 15*4+5 = 65，即 65×65 的滤波范围，与 64×64 已经非常相似。

A-SVGF [2018]

改进了 SVGF 的 temporal filtering 操作，先计算出 temporal gradient（时域梯度，可以理解成表示 shading point 在两帧之间着色变化的程度），再根据此计算出每 pixel 做 temporal filtering 时的混合系数，而不非使用一个固定的混合系数，增强了结果的时序稳定性。

实际这个方法个人感觉非常不实用，因为做了一大堆 gradient 重建却只是为了计算一个历史混合系数，实际工业界里我们常用历史 GBuffer 和当前帧 GBuffer 的差异来指导历史混合系数。

估计 Temporal Gradient

temporal 样本的复用需要进行 reprojection，而 reprojection 有两种方法：

• back projection（后向投影）就是把本帧的 sample 投影到先前帧的位置：\(\overleftarrow{G}_{i, j}\)
• forward projection（前向投影）先前帧的样本投影到本帧：\(\overrightarrow{G}_{i-1, j}\)

定义第 i 帧的第 j 个像素的表面采样表示为 \(G_{i,j}\)

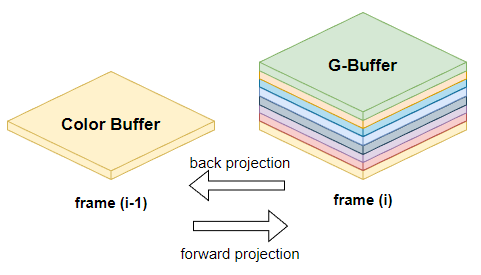
以前计算 motion vector 时，我们往往是使用 back projection，而在计算 temporal gradient 时我们使用了 forward projection。原因是本帧拥有的信息（G-Buffer）往往比上帧拥有的信息（例如最少的只有个 color buffer）多，使用 forward projection 的时候就可以有更多参考信息。

但实际上保存多一个历史帧 GBuffer 也无伤大雅，本文假设的情况是只能保存少量的历史帧信息（例如更低分辨率的 GBuffer）。

介绍完上面前置的知识后，这里定义 \(f\) 为着色函数，那么 temporal gradient 则可以表示为：

\[\delta_{i, \vec{j}}=f_{i}\left(\vec{G}_{i-1, j}\right)-f_{i-1}\left(G_{i-1, j}\right) \]

在上一帧渲染的收尾阶段时，我们可以将屏幕分成若干个 tile，每个 tile 抽取一个 pixel \(G_{i-1}\) 作为历史样本，并将历史样本列表传递给本帧（也就是它的下一帧），该列表样本实际上就是一个 \(\frac{1}{n}\) 低分辨率且阉割版的 GBuffer（包含 position 和 transform ID）。

在本帧，我们对历史样本列表的所有样本进行 forward projection，找到它们对应在本帧的位置 \(\vec{G}_{i-1, j}\)

也就是说上一帧保留的信息有：Color Buffer + \(\frac{1}{n}\) 分辨率的 GBuffer（每个 texel 只需要带 position 属性 + transform ID 属性） + 所有物体的 transforms

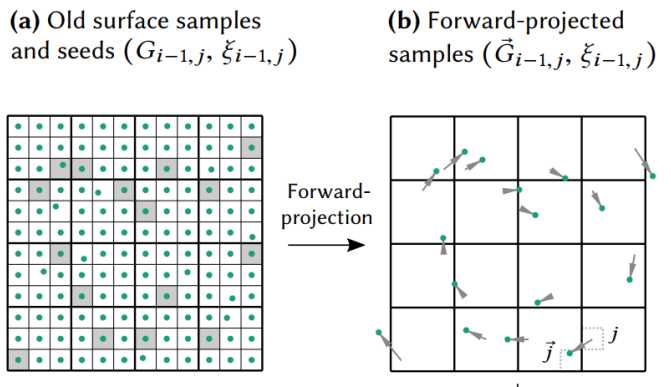
虽然对所有历史 pixels（完整分辨率的历史 GBuffer）作 forward projection 能获得质量更好的 temporal gradient，但这样需要开销增大太多不值得；而稀疏的历史 pixels 样本足以在低开销的情况下估计并重建出够用的 temporal gradient（无需太精确）。

然后，对应本帧的位置 \(\vec{G}_{i-1, j}\) + 利用本帧的 G-Buffer 信息并重新着色得到着色结果 \(f_{i}\left(\vec{G}_{i-1, j}\right)\)

同时，历史样本 \(G_{i-1}\) + 直接利用上一帧 color buffer 不做任何插值就能直接索引找到着色结果 \(f_{i-1}\left(G_{i-1, j}\right)\)

稳定的随机采样：我们还希望 temporal gradient 的方差不要过大（更少的噪声），即对上一帧 \(G_{i-1}\) 的着色与 forward projection 后重新的着色之间的变化尽可能少受些噪声干扰。

\[\begin{array}{r} \operatorname{Var}\left(\delta_{i, \vec{j}}\right)=\operatorname{Var}\left(f_{i}\left(\vec{G}_{i-1, j}, \xi_{i, j}\right)\right)+\operatorname{Var}\left(f_{i-1}\left(G_{i-1, j}, \xi_{i-1, j}\right)\right) \\ -2 \cdot \operatorname{Cov}\left(f_{i}\left(\vec{G}_{i-1, j}, \xi_{i, \vec{j}}\right), f_{i-1}\left(G_{i-1, j}, \xi_{i-1, j}\right)\right) \end{array} \]

而这其中着色函数可能依赖于随机数 \(\xi\)（例如path tracing 时随机数会用于选择采样方向），我们就需要减少随机数带来的干扰。

为此，应当保持 forward projection 后也依赖于相同的随机数，即令 \(\xi_{i-1,\vec{j}}:=\xi_{i-1, j}\)。这样我们的历史样本还需要存储上对应的随机数种子 \(\xi_{i-1, j}\)

这样，每个样本位置对应的 temporal gradient 就能算出来了：\(\delta_{i, \vec{j}}=f_{i}\left(\vec{G}_{i-1, j}\right)-f_{i-1}\left(G_{i-1, j}\right)\)

接着，就需要根据这些稀疏的 temporal gradient 样本，重建出稠密的 temporal gradient 2D texture。

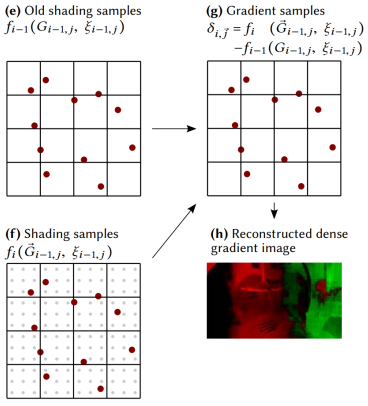
重建 Temporal Gradient Texture

稀疏的 temporal gradient 样本可以看成是 image 中几个特别亮的 texel，而我们可以利用 joint bilateral filtering 的思路插值出来得到一张 temporal gradient 2D texture。

重建过程中几个要点：

• 初始 temporal gradient image 全部 texel 的梯度值设置为 0（全黑），除了 temporal gradient 样本位置所在的 texel 是亮点（含有梯度值）

• 滤波范围需要大一些（因为样本稀疏）

• 需要多次迭代的联合双边滤波：

  \[\hat{\delta}^{(k+1)}(p)=\frac{\sum_{q \in \Omega} h^{(k)}(p, q) w^{(k)}(p, q) \hat{\delta}^{(k)}(q)}{\sum_{q \in \Omega} h^{(k)}(p, q) w^{(k)}(p, q)} \]

个人的奇思妙想：不知道 temporal gradient 是否能再利用 temporal 思想，混合上一帧的 temporal gradient，来得到更加精确的 temporal temporal gradient ？

计算 Temporal 混合系数

已经有了重建好的 temporal gradient image，现在我们要控制时序滤波的因子了，首先加入标准化因子：

\[\Delta_{i, \vec{j}}=\max \left(f_{i}\left(\vec{G}_{i-1, j}, \xi_{i-1, j}\right), f_{i-1}\left(G_{i-1, j}, \xi_{i-1, j}\right)\right) \]

因为空的层梯度设置为了 0，并使用了联合双边滤波产生 \({\hat{\Delta}_{i}(p)}\)，我们定义密度和标准化历史权重（该式意义在于让 \(λ\) 小于等于 1）：

\[\lambda(p):=\min \left(1, \frac{\left|\hat{\delta}_{i}(p)\right|}{\hat{\Delta}_{i}(p)}\right) \]

最后我们定义的 adaptive temporal 的混合系数为：

\[\alpha_{i}(p):=(1-\lambda(p)) \cdot \alpha+\lambda(p) \]

不同种类信号的 Filtering

color 信号实际上往往是由若干种信号调制而成，前面提到的 filtering 大都是在对调制后的 color 信号再进行 filtering，但如果我们可以在调制前拆分出这若干种信号并分别进行 filtering 后再调制，往往取得的降噪效果是更好的，原因如下：

• color 信号实际上是包含了无噪声的信号和有噪声的信号。如果拆分得当，我们就只需要对有噪声的部分信号进行 filtering，降噪效果会好很多（因为解调出无噪声部分后，剩余的信号函数往往会更加平滑）。
• 对不同拆分的信号类型，我们可以针对性使用不同的 filtering 方法，从而增强降噪效果。

Shadow Filtering

direct illumination = \(\sum_{n}\) direct lighting(n) * shadow factor(n)，n 为光源数量。

因此我们可以拆分出 shadow factor 信号并进行 filtering。并且由于 shadow 的特性，我们不需要对整个 shadow factor 图像进行 filtering，而只用对 shadow 边缘（软阴影部分）做 filtering。

详细做法可见 实时光线追踪（2）降噪：Nvidia Real-time Denoiser - KillerAery - 博客园 (cnblogs.com) 中的 tile-based denoising 章节。

Indirect Diffuse Filtering

indirect illumination 的 diffuse color 就是等于 irradiance / PI * albedo，因此我们可以利用 G-Buffer 解调出无噪声的 albedo 信号，从而只用对更平滑的 irradiance 信号（而非 indirect diffuse color 信号）做 filtering。

当然实际中，往往是在计算完 indirect irradiance 后不应用 albedo，而是做了 filtering 后再应用 albedo。

• 基于 normal + irradiance 的 filtering：根据本 pixel 法线对应半球范围与复用 pixel 法线对应半球范围的重合比例来决定 irradiance 的混合权重。

  此外对于 temporal filtering，需要额外记录历史帧 normal + irradiance。

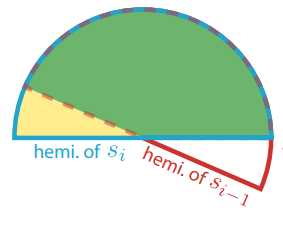
Indirect Specular/Glossy Filtering

indirect illumination 的 specular/glossy color 不像 diffuse color 那样很方便就能直接解调出 BRDF 部分（diffuse 信号与出射方向无关，而 specular 有关），为此可以有两种思路：

• 基于 normal + n 个 irradiance 的 filtering：使用 n 个圆锥立体角来粗略表示在不同方向上的 irradiance 强度信息（粗略代表了 shading point 在这个立体角范围接受的 irradiance），相当于拥有 n 个需要做 filtering 的信号；很显然，该方法需要增加 n 倍的 filtering 开销，并且由于 n 有限，也只能做粗略的 glossy filtering，对高精度的 specular 还是不推荐使用。

  此外对于 temporal filtering，需要记录历史帧 normal + n 个 irradiance。

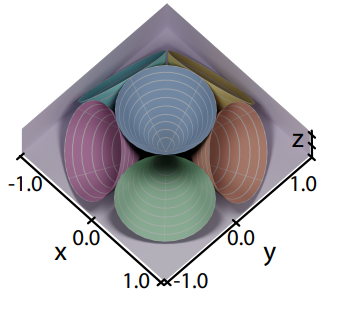
• 另外一种思路，在后面的“基于 BRDF 预积分的信号解调 [2021]”章节中将会详细描述如何解调出近似的 BRDF 部分，从而只用对剩余部分进行降噪，但是可能效果上会稍微有偏。

Radiance Filtering

前面对 indirect diffuse 还是 indirect specular/glossy 的 filtering，都是希望对 color 拆分出无噪的 BRDF 部分和剩余的 lighting 部分，然后对 lighting 部分做降噪（lighting 部分往往是一种 irradiance，可以感性理解成接受光照的总和）。

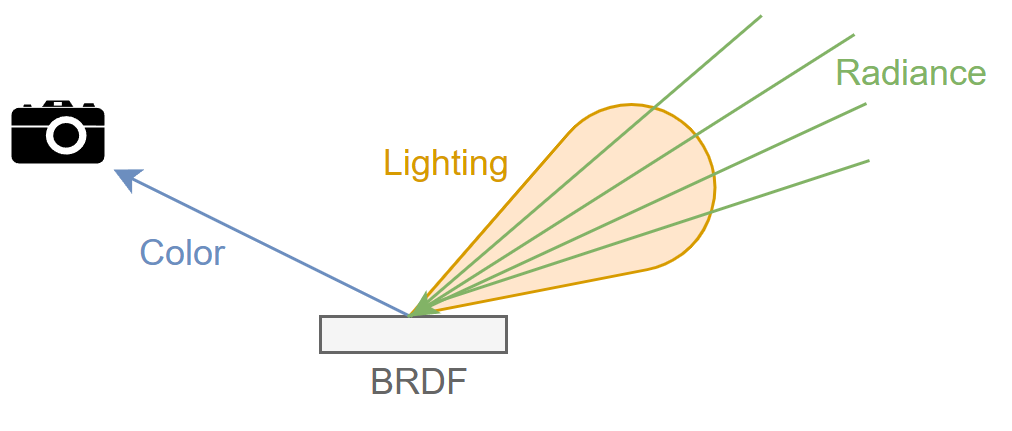
而 radiance filtering 的思路更进一步，对 incident ray 的 radiance 做 filtering，常用于 indirect specular/glossy 算法。我们假设每个 pixel 有一定数量的 rays（一般为 1 spp），并通过 BRDF 来做 importance sampling。

• 直接复用空间上相邻 pixels 的 rays 作为本 pixel 的额外 rays，从而增加蒙特卡洛积分的样本数。

  也就是说原来对 color 做 filtering 是相当于下式：

  \[\begin{aligned} & \widehat{L_o}\left(x, \omega_o\right)=\sum_j w_j f_r\left(x_j, \omega_{i, j}, \omega_{o, j}\right) L_i\left(x_j, \omega_{i, j}\right)\left(n_j \cdot \omega_{i, j}\right) \end{aligned} \]

  而对 radiance 做 filtering 则相当于下式：

\[\begin{aligned} \widehat{L_o}\left(x, \omega_o\right)=\sum_j w_j f_r\left(x, \omega_{i, j}, \omega_o\right) L_i\left(x_j, \omega_{i, j}\right)\left(n \cdot \omega_{i, j}\right), \end{aligned} \]

相邻 pixels 的 BRDF 相差越大，那么引入的 bias 就越大（因为 BRDF pdf 不匹配，更具体来说就是存在相邻 pixel pdf = 0 而本 pixel pdf 为非 0 值的样本域）。在实践中可以通过比较 pixels 几何相似性来决定额外 ray 的权重（甚至极度不同的情况下可以直接丢弃 ray），从而尽可能减轻 bias。

另外，也需要为每个额外 ray 重新计算 BRDF 项（n 个额外 ray = n 次计算 BRDF），这可能带来一定的计算开销。

• ray reconstruction：当采用低于 1 spp 的 ray tracing 时，会有一些 pixels 缺失 ray 信息，此时可以利用时序上或空间上相邻且有 ray 信息的 sample pixels，根据 BRDF lobe 相似性来重建本 pixel 的 ray（主要是重建出 ray 的 radiance 和 hit distance）。

DLSS 3.5 基本原理便是 ray reconstruction，只是额外引入了神经网络方法。

更可靠的 Motion Vectors [2021]

motion vector 并不总是存在或无效，强行应用就会出现鬼影（随着时间的推移，不合理的泄漏或阴影滞后）：

• 背景中的静态位置可能被前一帧的运动物体遮挡。
• 对于 shadow, glossy reflection 效果，motion vector 可能是错误的（例如 receiver 具有长度为 0 的 motion vector，但投射到其上的 shadow 可能随光源任意移动）

本 paper 并没有结合这三种 motion vector 来使用，只是分别在三种应用场景分别单独使用 shadow，glossy，dual 测测结果。如果要落地的话，可以考虑分开多种信号并分别使用不同的 temporal filtering 来处理：

• 对于 RT shadow 产生的 visibility 信号，可以使用基于 shadow motion vector 的 temporal filtering。
• 对于 GI 产生的 indirect specular 信号，可以使用基于 glossy motion vector 的 temporal filtering。
• 对于绝大部分信号（尤其 indirect diffuse 信号），均可使用基于 dual motion vector 的 temporal filtering 以取代传统 motion vector。

Shadow Motion Vector

Percentage Closer Soft Shadows (PCSS) 需要 shading point 发射若干 rays 来检测可以打到面光源的通过率（也就是 visibility），也就是说需要往 light 采样多次。我们期望利用时序上（上一帧）的样本来增加 PCSS 的采样数。

具体步骤：

1. 在本帧，让 shading point 投射一条 shadow ray 打到 light 上，并记下可能穿过 blocker 的点 \(b_i\) 和打到光源面上的点 \(l_i\)
2. back projection ：\(b_i\) 通过本帧 blocker 的逆变换 \(T^{-1}_i\) 和上一帧 blocker 的变换 \(T_{i-1}\) 得到 \(b_{i-1}\) ；同理 \(l_i\) 也能得到 \(l_{i-1}\)
3. 以 \(s_i\) 和其法线 \(n_{s_i}\) 构造一个无限长平面，然后将 \(l_{i-1}\) 与 \(b_{i-1}\) 连成线后相交于该平面，算出该相交点 \(s_{i-1}\)

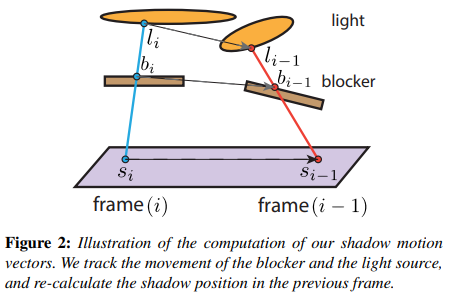
4. 把 \(s_{i-1}\) 投影到本帧 camera 的屏幕中，并得到屏幕 uv 后根据 depth buffer 重建出实际被看到的 shading point 位置 \(s^V_{i-1}\)，也就是说计算出的 motion vector = \(s^V_{i-1}-s_{i-1}\)

5. 此外，当 \(s^V_{i-1}\) 与 \(s_i\) 真的如假设那样在同一平面，那么这个 motion vector 极大概率是准确的，也就是说采样历史帧时可以参考 \(s^V_{i-1}\)；否则，就不应该过多参考 \(s^V_{i-1}\)

   为此，可以根据 \(\theta\) （\(s_i\) 法线与 motion vector 的夹角）来实现加权的 temporal 混合，这样当 \(\theta\) 与 \(\frac{\pi}{2}\) 相差很大时就可以相当于拒绝采样历史帧样本。

   weight：

\[ \alpha^{V}=1-G\left(\theta-\frac{\pi}{2} ; 0,0.1\right) \cdot(1-\alpha) \]

\(cos \theta = \frac{n_{s_i} \cdot (s^V_{i-1}-s_i)}{|s^V_{i-1}-s_i|}\)

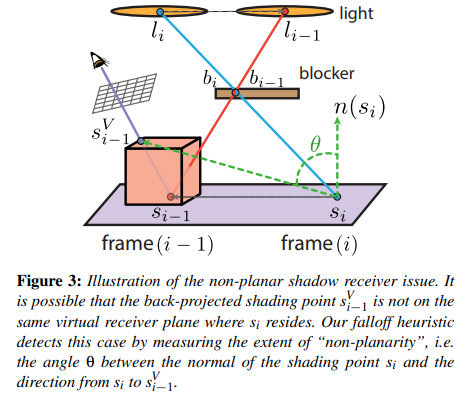
不过采样结果是稍微 noisy 的，因此还需要一些 clean-up filter。

Glossy Motion Vector

对于 glossy motion vector，也是类似思想。我们期望利用时序上（上一帧）的样本来增加 glossy reflection 的采样数。

具体步骤：

1. 在本帧，让 shading point 根据 BRDF importance sampling 来生成一条 ray 并打到某个 mesh 上，并记下 hit point \(h_i\)
2. back projection ：\(h_i\) 通过本帧 mesh 的逆世界变换 \(T^{-1}_i\) 和上一帧 mesh 的世界变换 \(T_{i-1}\) 得到 \(h_{i-1}\)
3. 以 \(s_i\) 和其法线 \(n_{s_i}\) 构造一个无限长平面，然后将 \(h_{i-1}\) 于该平面翻转（类似形成一个倒置的虚像），并连接 camera point，算出与该平面的相交点 \(s^C_{i-1}\)

因为 glossy lobe 的中心方向是最强烈的反射方向，因此可以假设退化成纯镜面反射方向，就能得到反射率最高的 shading point

4. 以 \(s^C_{i-1}\) 为中心，邻近的 shading point 都可以作为采样的参考（根据 \(s^C_{i-1}\) 的材质 roughness 程度决定半径），并且对这一圈的样本按高斯分布的方式去加权采样结果作为历史帧的 color
5. 类似 shadow motion vector，利用 \(\theta\) 检测共平面的程度，当 \(\theta\) 与 \(\frac{\pi}{2}\) 相差很大时就可以相当于拒绝采样历史帧样本

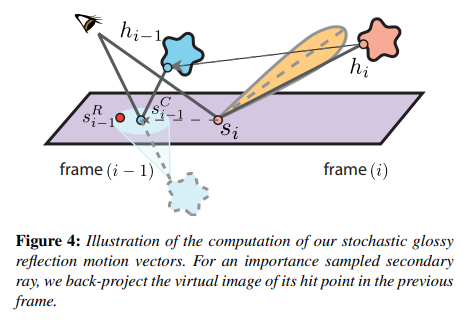
Dual Motion Vector

假设在本帧 pixel \(x_i\) 可见，而在上一帧它被 occluder \(y\) 遮挡住了。

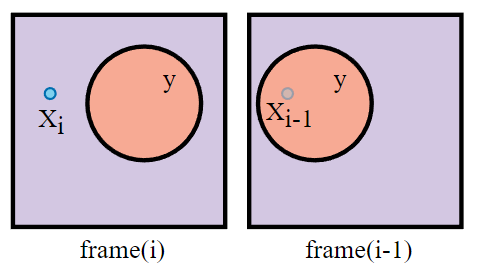
传统 motion vector ：

1. 对本帧 \(x_i\) 进行 reprojection 得到对应上帧的位置 \(x^o_{i-1}\)（但其实 \(x^o_{i-1}\) 是投影在了上帧的 occluder \(y\) 上，因此得到的上帧 color 是 occluder \(y\) 的 color）
2. 强行混合本帧 \(x_i\) 的 color 和上帧的 color，这也是造成鬼影的一大原因

dual motion vectors：基于假设要渲染的 pixel 和 occluder 的相对位置不变。

1. 对本帧 \(x_i\) 进行 back projection 得到对应上帧的位置 \(y\)
2. 再将上帧 \(y\) 进行 forward projection （需要借助历史 id buffer）得到对应本帧的位置 \(z\)
3. 计算相对位移 \(offset = x_i-z\)
4. 那么最终找到的对应上帧位置便是 \(x^o_{i-1} = y + offset\)
5. 混合本帧 \(x_i\) 的 color 和上帧 \(x^o_{i-1}\)

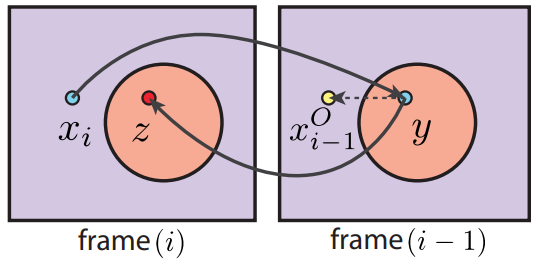
对于没有遮挡物的案例来说，\(offset\) 往往是 0，即用了 dual motion vectors 会退化成传统 motion vector：

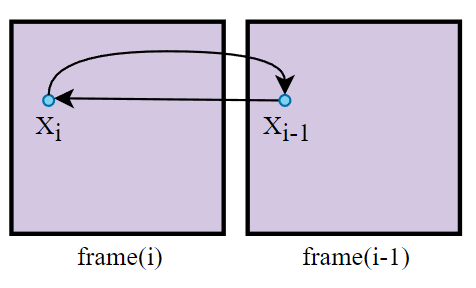
为什么要假设渲染的 pixel 和 occluder 的相对位置不变？

这是因为，根据相对位置算出来的上帧位置虽然一般不是该 pixel 以前的真正位置，但是该位置很大概率是位于与该 pixel 处在同一平面的邻近位置，而这些位置得到的 color 和 pixel 得到的 color 就很大相似度，有一定参考价值。

个人想法：既然有历史 id buffer，其实这个方法在最后的步骤也可以结合 id detection 方法，通过比较 pixel 的历史 id 和当前 id 来进一步规避边缘情况。

基于 BRDF 预积分的信号解调 [2021]

平时我们做 filtering 都是对 color \(C\) 做的，而 \(C\) 就是渲染方程中的 \(L(\omega_o)\)：

\[\bar{C} = \operatorname{denoised}\left[C\right] \]

\[C = L\left(\omega_o\right) =\int_{\Omega} f_r\left(\omega_i, \omega_o\right) L\left(\omega_i\right) \cos \theta_i \mathrm{~d} \omega_i \]

而这篇 paper 尝试将渲染方程中的 BRDF 部分解调出来：

\[\begin{aligned}L\left(\omega_o\right) & =\int_{\Omega} f_r\left(\omega_i, \omega_o\right) L\left(\omega_i\right) \cos \theta_i \mathrm{~d} \omega_i \\ & = F_\beta\left(\omega_o\right) \cdot \frac{\int_{\Omega} f_r\left(\omega_i, \omega_o\right) \cos \theta_i L\left(\omega_i\right) \mathrm{d} \omega_i }{F_\beta\left(\omega_o\right)}\\ & = F_\beta\left(\omega_o\right) \cdot L_W\left(\omega_o\right) \end{aligned} \]

其中，解调出来的部分（即 BRDF 部分积分）为 \(F_\beta\left(\omega_o\right)\) 。而剩余的部分组成了我们需要进行 filtering 的 lighting 信号 \(L_W\left(\omega_o\right)\) 。

最后，只对渲染方程中剩余的部分进行滤波，并重新调制回 color：

\[\bar{C} = F_\beta\left(\omega_o\right) \operatorname{denoised}\left[\hat{L}_W\left(\omega_o\right)\right] \]

效果图：

个人剖析（嫌长可跳过）：

paper的核心想法就是假设渲染方程可约等于 BRDF 部分积分和 lighting 部分积分相乘（实际就是 IBL 中的 split sum 方法）：

\[\begin{aligned}\int_{\Omega} f_r\left(\omega_i, \omega_o\right) L\left(\omega_i\right) \cos \theta_i \mathrm{~d} \omega_i & \approx \frac{\int_{\Omega_{f_{r}}} L_{i}\left(\omega_{i}\right) \mathrm{d} \omega_{i}}{\int_{\Omega_{f_{r}}} \mathrm{~d} \omega_{i}} \cdot \int_{\Omega^{+}} f_{r}\left(\omega_{i}, \omega_{r}\right) \cos \theta_{i} \mathrm{~d} \omega_{i} \\ & = \frac{\int_{\Omega_{f_{r}}} L_{i}\left(\omega_{i}\right) \mathrm{d} \omega_{i}}{\int_{\Omega_{f_{r}}} \mathrm{~d} \omega_{i}} \cdot F_\beta\left(\omega_o\right) \end{aligned} \]

那本 paper 的滤波行为就能将 BRDF 部分完美解调出来，而只用对真正意义上的 lighting 部分做滤波：

\[\begin{aligned} L_W\left(\omega_o\right) &= \frac{\int_{\Omega} f_r\left(\omega_i, \omega_o\right) \cos \theta_i L\left(\omega_i\right) \mathrm{d} \omega_i }{F_\beta\left(\omega_o\right)} \\& = \frac{\int_{\Omega_{f_{r}}} L_{i}\left(\omega_{i}\right) \mathrm{d} \omega_{i}}{\int_{\Omega_{f_{r}}} \mathrm{~d} \omega_{i}} \end{aligned} \]

然而实际上，这个假设是建立在近似公式上的，想让这个公式近似效果比较精确，那么需要满足以下一种或两种条件：

• 积分域 \(\Omega_G\) 比较小
• \(g(x)\) 比较光滑，即变化不是很大

这两个条件实际上就是分别对应两种理想情形：

• 如果 BRDF 是 specular 的，那么它的 lobe 往往比较尖锐，即只有很小的积分域才能接受环境光。
• 如果 BRDF 是 diffuse 的，那么它的 lobe 往往是均匀的半球状，即无论哪个方向的环境光打进来， \(f_r\) 函数的输出几乎没多少变化（甚至是个常数）。

但实际情形往往没有这么完美，因此这个近似公式会产生偏差，得到的 \(L_W\left(\omega_o\right)\) 实际上也不会刚好分子分母 \(F_\beta\left(\omega_o\right)\) 相抵消，因此会引入bias（主要来源于该渲染方程的解调并没有考虑 specular occlusion）。

BRDF 预积分

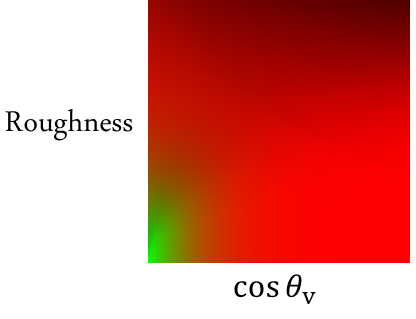
\(F_\beta\left(\omega_o\right)\) 便是解调出来的 BRDF 部分积分，跟 IBL 的 split sum 一模一样。

\[F_\beta\left(\omega_o\right)=\int_{\Omega} f_r\left(\omega_i, \omega_o\right) \cos \theta_i \mathrm{~d} \omega_i \]

为这个 BRDF 积分预先建立一张 2D LUT。在后续查表的时候，输入的两个参数 roughness 和 \(w_o\) ，就能得到对应的 \(F_\beta\) 值。

Lighting Filtering

接下来我们就只需要对每个 pixel 正常使用蒙特卡洛来计算出 lighting 积分：

\[L_W\left(\omega_o\right)=\int_{\Omega} \frac{f_r\left(\omega_i, \omega_o\right) \cos \theta_i L\left(\omega_i\right)}{F_\beta\left(\omega_o\right)} \mathrm{d} \omega_i \approx \frac{1}{F_\beta\left(\omega_o\right)} \cdot\sum_k \frac{f_r\left(\omega_i, \omega_o\right) \cos \theta_i L\left(\omega_i^{(k)}\right)}{p\left(\omega_i^{(k)}\right)} \]

再对 lighting 信号 \(\hat{L}_W\left(\omega_o\right)\) 进行滤波（可以搭配任何滤波方法，如 SVGF），再乘回 BRDF 预积分部分即可。

\[\bar{C} = F_\beta\left(\omega_o\right) \operatorname{denoised}\left[\hat{L}_W\left(\omega_o\right)\right] \]

结论：在我复现该算法后，虽然在物体表面上确实发现能保留一定的材质细节，然而对总体效果而言降噪作用微乎其微，并且还可能会引入一些过亮的边缘（因为 specular BRDF 积分在 grazing angle 下往往会很大），本质上就是因为算法有 bias 并且没有考虑 specular occlusion。

其它 [TODO]

Outliers Removal

可以根据空间上邻域 pixels 的值来算出一个 min/max 或者 variance，然后由此去 clamp 掉颜色差异较大的 pixel 样本（例如一些亮点）。当然直接粗暴的剔除这些亮点可能会导致能量不守恒，但是最高效的减少 firefly 方法就是如此。

ID Detection

通过 id（一般是 mesh id + instance id）来决定是否混合目标 pixel。

• 这对于 temporal filtering 来说尤其重要，因为可以通过判断前后两帧 motion vector 对应的 pixel 对应的物体是否为一个物体：如果不是同一物体，混合系数 \(\alpha\) 设为 0；这样能够大大减轻鬼影（ghosting）问题。

Clampping [TODO]

动静像素差异处理 [UFSH2023]

《鸣潮》的 TAAU 方案中为了实现静态像素更稳定，动态像素更清晰，采用了两种策略：

1. 像素的 velocity 越快，则历史权重越低。

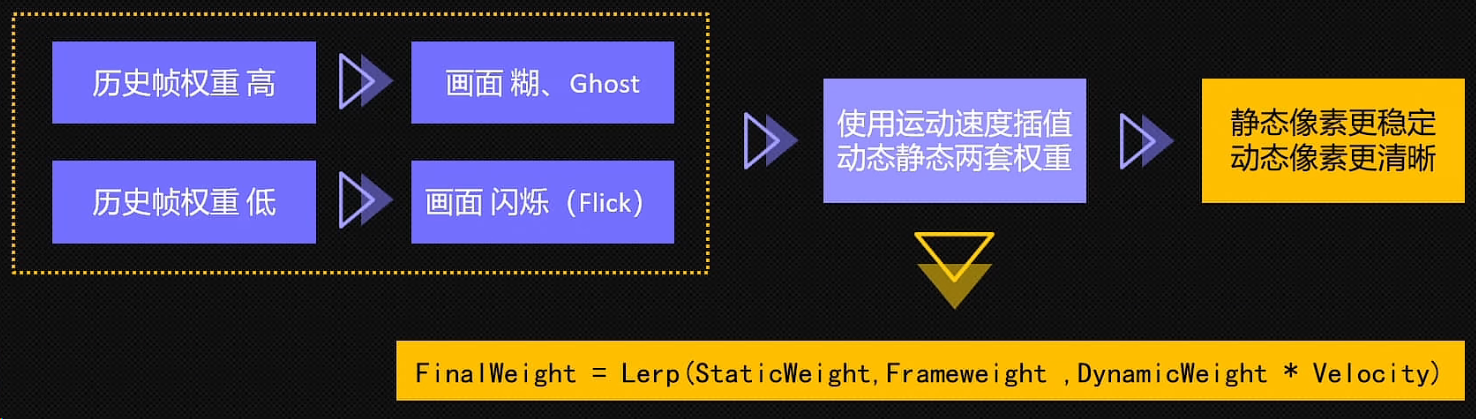
2. 像素的 velocity 越快，则越混合锐化结果，锐化滤波核用的是：

   \[\begin{equation} \left[ \begin{array}{ccc} 0 & -1 & 0 \\ -1 & 5 & -1 \\ 0 & -1 & 0 \end{array} \right] \end{equation} \]

   这个锐化滤波的五个样本刚好是可以复用的，减少读取 history texture 的次数。

参考

• [1] GAMES202-高质量实时渲染-闫令琪
• [2] Temporally Reliable Motion Vectors for Real-time Ray Tracing | EuroGraphics 2021
• [3] Spatiotemporal Variance-Guided Filtering: Real-Time Reconstruction for Path-Traced Global Illumination | HPG 2017
• [4] Gradient Estimation for Real-Time Adaptive Temporal Filtering | 2018
• [5] A-SVGF 论文分析
• [6] 光线追踪降噪技术 2020
• [7] Edge-Avoiding À-Trous Wavelet Transform for fast Global Illumination Filtering | HPG 2010
• [8] Real‐time Denoising Using BRDF Pre‐integration Factorization | Computer Graphics Forum 2021
• [9] Radiance filtering for interactive path tracing | ACM SIGGRAPH 2012
• [10] [UFSH2023]《鸣潮》基于虚幻引擎4的多平台效果和性能优化实践 | 库洛游戏