基于屏幕空间的实时全局光照（Real-time Global Illumination Based On Screen Space）

所谓基于屏幕，就是指利用的信息来源于“屏幕”，例如：frame buffer、depth buffer、G-buffer 都记录着屏幕所看到的各 pixel 的信息。

Reflective Shadow Maps（RSM）

Reflective Shadow Maps（RSM）：主要是利用了类似 shadow map 思想的GI技术，但 shadow map 严格意义上不属于用户的“屏幕”信息，而是属于光源的“屏幕”信息，为了懒得再写多一篇博客分类，我还是将其归纳为 screen space 的技术。

RSM的思路：将受到直接光照的地方都视为次级光源，那么 shading point x 所受的次级光照便是来源于各个次级光源的反射。

次级光照 = bounce 为1的间接光照，RSM算法只能支持 bounce 为 1 的间接光照效果

然后，假定次级光源均是 diffuse 物体，那么一小块次级光源 patch（这块次级光源面积位于点 \(x_p\) ）对 shading point x 的 irradiance 贡献是：

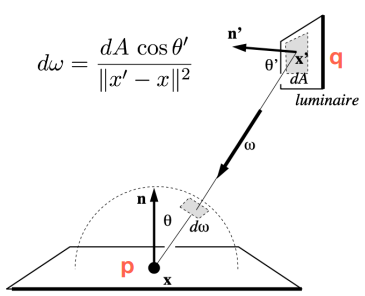
\[E_{p}(x) = \Phi_p \frac{\max (\mathbf{n_p} \cdot normalize(x-x_p),0)\max (\mathbf{n} \cdot normalize(x_{p}-x),0)}{\left\|x-x_{p}\right\|^{2}} \]

\(\Phi\) 是次级光源 patch 的 radiant flux，\(\mathbf{n_p}\) 是 \(x_p\) 的法线，\(\mathbf{n}\) 是 \(x\) 的法线

所有的次级光源 patch 对 \(x\) 的贡献加起来便是 \(x\) 的间接光照 irradiance：

\[E(x) =\sum \ E_{p}(x) \]

那么，怎么找到这些次级光源呢？这就用到了 shadow map 的思想：

阴影生成 pass：在光源摄像机渲染 shadow map （往往只记录了深度）的时候，顺便额外记录 世界坐标 \(x_p\) 、法线 \(n_p\)、接受的直接光源 radiant flux \(\Phi_p\)。那么就可以认为 shadow map 的一个 texel 对应一块patch ，从而这张 shadow map 就包含了所有次级光照 patch 的信息了。

实际上，世界坐标也可以通过uv坐标、遮挡深度来推算得到，好处是可以节省空间，坏处那自然是没那么精确了。

此外，计算一个 texel （或者说一块patch）的 \(\Phi_p\) 时，无论光源是directional light还是spot light，都不必计算 cosine 或者距离衰减，而直接用光源强度与物体 albedo 相乘

\[\Phi_p=\Phi(u_p,v_{p})= I * c_p \]

\(u_p、v_p\) 为 \(x_p\) 在 shadow map 上的纹理坐标。

主渲染pass：在 pixel shader 阶段，计算出 \(x\) 对应的 shadow map uv坐标，并取该坐标周围若干个 texel （这些正是我们要采样的次级光源点）对应的 世界坐标 \(x_p\) 、法线 \(n_p\)、接受的直接光源radiant flux \(\Phi_p\) ，它们将对 \(x\) 的渲染造成间接光照影响：

\[L_{indirect}(x,\mathbf{v}) = \frac{E(x)}{\pi} = \frac{{\sum_{\text {texels p}} \ E_{p}(x)}}{\pi} \]

RSM效果图：

RSM 重要性采样

理论上，为了实现最好的RSM效果，应当取整张 shadow map 的所有 texel 作为次级光源点，因为整张shadow map 意味着包含了整个光源照到的信息。但这样所需的采样数就相当于 shadow map 的分辨率，代价太高。

因此我们应当使用少量的采样数来保证性能，同时也要保证RSM的间接光源质量能够接受，那么就容易想到用 Importance Sampling 来加速采样的收敛。那么哪些地方的次级光源点比较重要呢？

RSM 假定，离 shading point x 近的点更可能给 x 的光照贡献大，而远的点给 x 的光照贡献小。

因此这个用于RSM的 Importance Sampling 将给近的的地方更多的采样点（当然权重更小），远的地方更少的采样点（权重更大），用可视化采样点数量和权重大概就是这个样子：

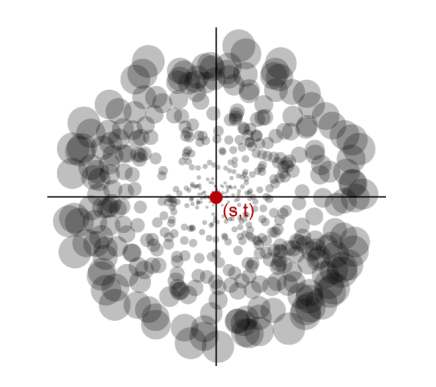
因此，选取一个随机采样点坐标 \((u,v)\) 和对应的权重 \(importance\)：

\[(u,v)=\left(s+r_{\max } \xi_{1} \sin \left(2 \pi \xi_{2}\right), t+r_{\max } \xi_{1} \cos \left(2 \pi \xi_{2}\right)\right) \]

\[importance = (\xi_{1})^2 \]

其中，\(s、t\) 为 shading point x 在 shadow map 的纹理坐标，\(\xi_{1}、\xi_{2}\) 为随机数

RSM 的应用与缺陷

缺陷：

性能开销与灯光数量成正比，有点昂贵（意味着需要同样数量的 shadow map、在多张 shadow map 采样等...）
由于 shadow map 记录的是光源摄像机屏幕上的表面几何信息，因此在计算 patch 对 shading point 的贡献时很难做到检查 visibility：

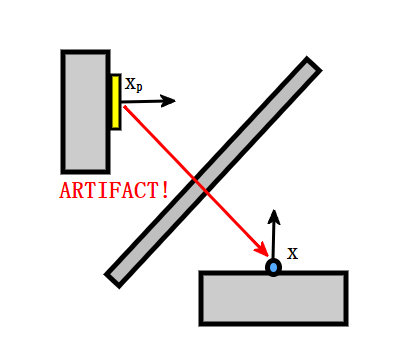
仅支持 one-bounce 间接光照效果
RSM 假设次级光源面均是 diffuse 的，这会影响图像的正确性（当然大部分情况下还是可以接受的）

应用：

作为廉价的GI方法，常被用于做单个重要光源的GI效果（例如手电筒）

Screen Space Ambient Occulsion（SSAO）

屏幕空间环境光遮蔽（Screen Space Ambient Occulusion,SSAO）：是一类游戏工业界很常用且廉价的屏幕空间 GI 方法。

所谓环境光遮蔽（AO），就是某个 shading point 因为被其它几何表面所遮挡，从而降低了接受环境光的比例（这种遮蔽常常发生在凹处表面）：

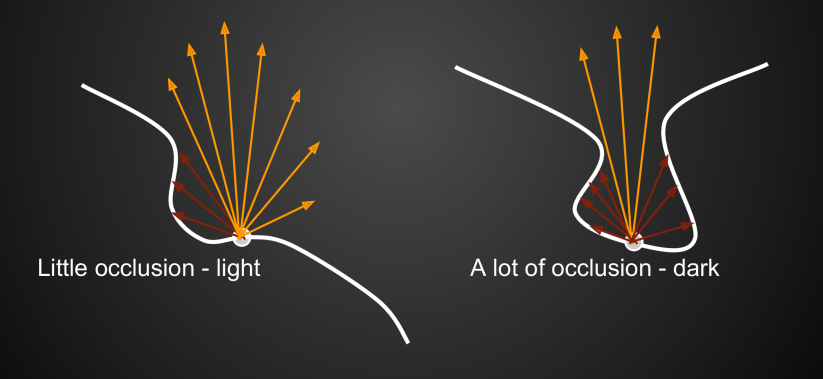
AO 的基本公式：

\[A(x) = 1-\frac{1}{\pi}\int{}V(x,w_i) cos\theta_i \mathrm{d}w_i \]

AO 往往只代表一个简单的光线入射遮挡比例，乘于它意味着需要把 shading point 当作 diffuse 的表面来看待（即与观察方向无关，出射到哪都是 \(\frac{1}{\pi}\) 的 irradiance）。

一种计算 AO 的经典方法就是通过蒙特卡洛 + ray casting 去预计算一个模型上各处的 AO，然后做成该模型的 AO texture 后就可以在运行时采样并与环境光照值相乘（AO texture 存的是 visibility 值）。

而 SSAO 不需要预计算过程，而只需要通过屏幕的 depth 信息就能做到还算不错的 AO 效果。

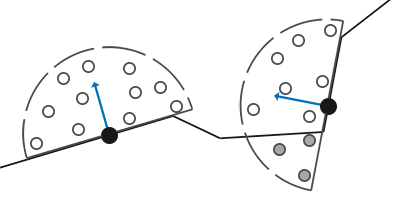
SSAO 的算法流程：对于某个 shading point ，

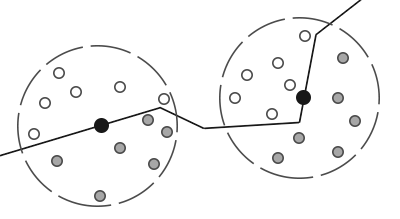
在该点一定半径内的球型范围内随机采样 N 个点，然后这些采样点将与 depth buffer 对应的深度作比较：若采样点的深度小于 depth buffer 对应位置的深度，则说明该采样点被遮蔽了
根据所有被遮蔽得到采样点数量 \(Occ\)，计算出 AO 为 \(A(p) = \frac{Occ}{N}\)
那么该 shading point 的环境光照即为

\[L_{indirect}(x) = \frac{1-A(x)}{\pi} \int_{\Omega^{+}} L_{\mathrm{environment}}\left(\mathrm{x}, \omega_{i}\right) {\rho} \cos \theta_{i} \mathrm{~d} \omega_{i} \]

\(\rho\) 为 albedo。

SSAO 效果图（左为关闭SSAO效果，右为开启SSAO效果，可以看到物体交界处等地方多了更多的暗部细节）：

SSAO Blur

实践中由于性能限制，SSAO 一般仅使用16个采样点，那么 AO 的结果将会是 noisy 的：

这时候就稍微修改下 SSAO 的算法流程，在计算 shading point 的 AO 时，不再直接乘于 color。而是先写入到一个 AO buffer 上，之后用一个屏幕后处理 pass 对 AO buffer 信息进行边缘保留滤波算法（其实就是保持边缘感的模糊操作，例如双边滤波算法），那么得到将是不那么 noisy 的 AO 结果：

SSAO 半球采样

实际上，渲染方程本就是上半球的积分，下半球的光线不会照到 shading point，因此 SSAO 采样范围不应该是一个球型，而应当是基于该点的法线为中心的半球形采样范围。

采样上半球采样范围的 SSAO 改进方法，得到该范围的采样点算法也很简单：

vec3 rand;				// 在球形上的随机坐标
vec3 n;					// shading point法线
rand = sign(dot(n,rand))*rand;	// 在半球上的随机坐标

SSAO 的应用与缺陷

缺陷：

仅包含屏幕表面的几何信息不能表示完全正确的 visibility，因此 AO 效果不那么准确（相对于预计算AO贴图）

例如，下图中间点的采样，有个红色采样点实际上没有被遮蔽。但是该采样点的深度小于depth buffer的对应深度，因此被 SSAO 判定为遮蔽了。

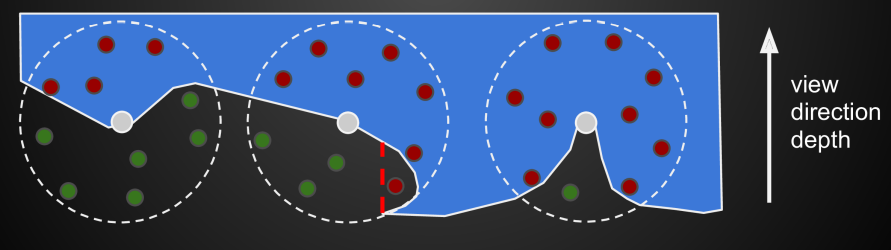
仅支持短距离的物体遮蔽效果

应用：

廉价的GI效果，提升画面的暗部细节，大部分游戏都会将其纳入一种画面增强选项，虽然之后有性能和效果更好的 HBAO 算法作为取代。

Screen Space Directional Occlusion（SSDO）

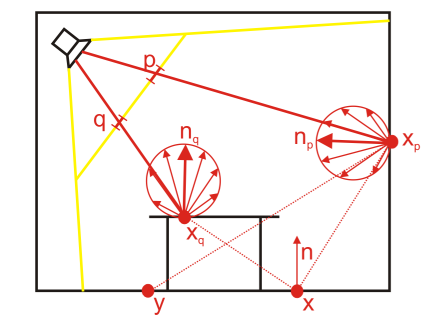
Screen Space Directional Occlusion（SSDO） 也是一类与 SSAO 极其相似的屏幕空间 GI 方法，区别在于它们看待光线遮蔽的角度是相反的：

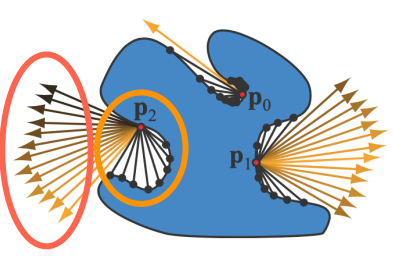
AO 认为 shading point 朝外的光线打到物体几何表面时，相当于外部环境光被这个表面遮挡了，因此（对于下面这幅图） AO 将红色部分视为间接光照来源，黄色部分视为损失的间接光照
而 DO 认为 shading point 朝外的光线打到物体几何表面时，相当于受到了表面的间接光照，因此（对于下面这幅图） DO 会将黄色部分视为间接光照来源，红色部分视为损失的间接光照

也因此，SSAO 往往增加的是明暗细节，而 SSDO 往往增加的是周围表面的颜色影响（或者说增加 color bleeding 效果）。

SSDO 需要依赖屏幕的 color, depth 信息来完成。

SSDO 算法流程的思路也和 SSAO 相似：对于某个 shading point，

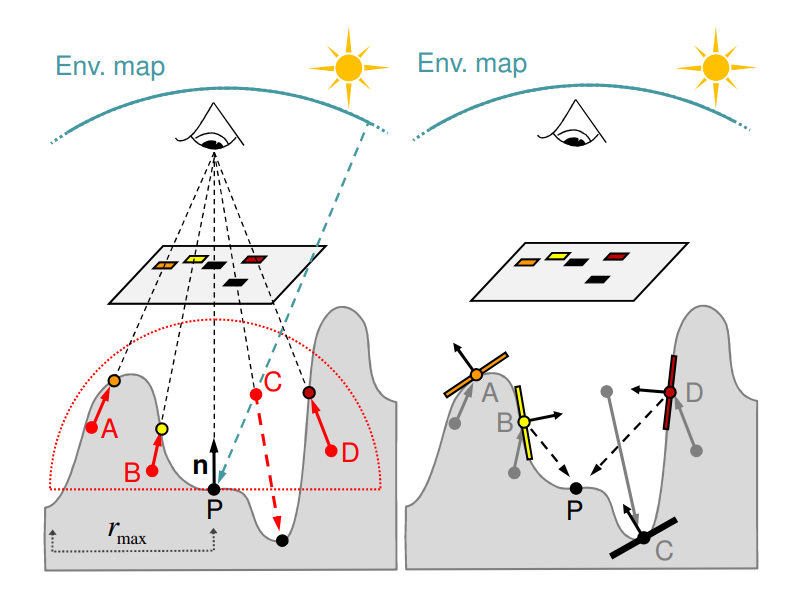
先在 shading point 一定半径内的半球型范围内随机采样 N 个点，然后这些采样点将与 depth buffer 对应的深度作比较：若采样点的深度小于 depth buffer 对应位置的深度，则说明该采样点被遮蔽了
对于每个被遮蔽的采样点，将该采样点对应的 pixel 视为次级光源 patch，对 shading point 造成间接光照的贡献：

SSDO 计算该 GI 的时候会把物体几何表面所有 pixels（也包括 shading point 本身）都将假设为 diffuse 表面

\[E_p(x) = L_{direct}(p)(1-V_p(x)) \frac{{Area}(p)\cos\theta_{s_i}\cos\theta_{r_i}}{d^2_i} \]

\(Area(p)\) 即为 pixel p 的片元面积，可以通过 p 的深度算出（p越远，对应的片元面积越大）

累积所有被遮蔽采样点的间接光照，得到该 shading point 的间接光照 irradiance，并以 diffuse 形式反射到眼睛里：

\[E(x) = \sum_{i=0}^N E_{p_i}(x) \]

\[L_{indirect}(x) = \frac{\rho}{\pi} E(x) \]

SSDO 效果图：

SSDO 的应用与缺陷

缺陷：

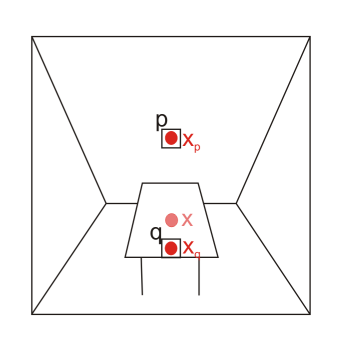
仅包含屏幕表面的几何信息仍然不能表示完全正确的 visibility，即会缺失屏幕看不到的平面信息（对于有颜色的GI效果很容易看出artifact）

仅支持短距离GI效果，而无法展示长距离的GI

仅支持 one-bounce 间接光照

Horizon Based Ambient Occlusion（HBAO）

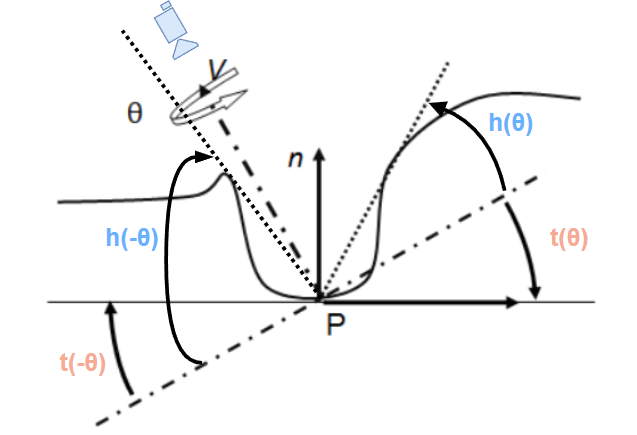
前面 SSAO 计算 AO 的方式太过耗费性能，因为它是基于估量面积覆盖率去计算 AO 的（样本是三维空间分布的），而为什么我们不能基于方向角覆盖率去计算 AO （样本是二维空间分布）呢？

HBAO 就是基于方向角覆盖率的思想出发：在 shading point 上往各个方向进行 ray casting，找到与 shading point 切平面夹角最大且 hit success（意味着遇到遮挡物）的 ray 方向，通过该 ray 方向和切平面的夹角 \(\alpha\) 就可以得到遮蔽率：

\[A = \int^{\alpha}_{\phi=0}\cos(\phi)\mathrm{d}\phi = \sin(\alpha) \]

不过，直接计算 \(\alpha\) 是挺耗的，需要将 ray 向量和切向量点积后进行反三角函数，因此原论文采取了一种更容易计算的近似方式：将 \(\alpha\) 拆成两部分，一部分是 ray 方向与 view 平面的角度差 \(h\) ，另一部分是切平面与 view 平面的角度差 \(t\)，其关系是 \(\alpha = h - t\)

在计算 ao cosine 贡献时，shading point 没有使用原来的 n 而是用 view 向量作为法向量，这样计算 AO 便可以：

\[A \approx \int^{h}_{\phi=t}\cos(\phi)\mathrm{d}\phi = \sin(h)-\sin(t) \]

HBAO 的具体算法流程为：

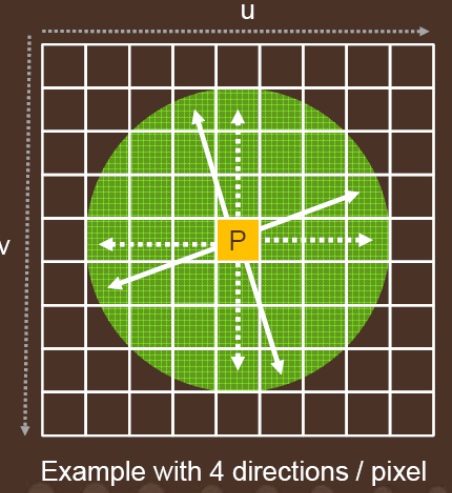
对于 shading point p，我们先屏幕空间上采样四个方向，它们对应 \(\theta_1\),\(\theta_2\),\(\theta_3\),\(\theta_4\) ：
- 初始的四个方向都是轴对齐的十字（虚线），然后对整个十字进行一个随机旋转角度，就可以得到当前帧的四个采样方向（实线）

对于某个采样方向 \(\theta\) ：
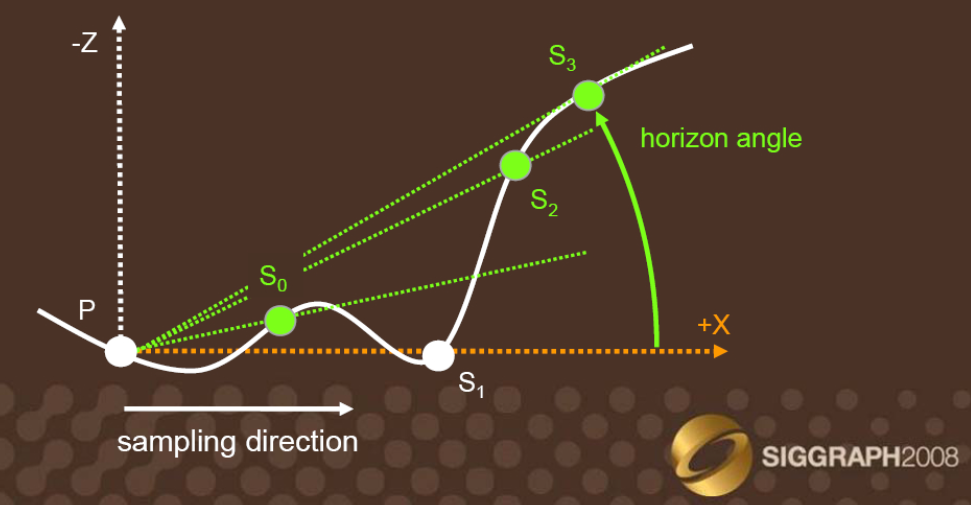
- shading point 上沿 \(\theta\) 方向进行 ray marching，最终找到可遇到遮蔽物与 view 平面最高仰角的 sin 值：
\[tan(h(\theta)) = \frac{RayDir.z}{\sqrt{(RayDir.x)^2+(RayDir.y)^2}} \]
\[\sin(h(\theta)) = \frac{\tan(h(\theta))}{\sqrt{1+\tan^2(h(\theta))}} \]

如下图例子，找到的最高仰角为 \(S_3\) 方向上的。
- 也顺便根据 ray tracing 结果对应的 hit dist \(r(\theta)\)，计算出本次 \(\theta\) 角切面的样本权重为：
  \[W(\theta) = max(0,1-\frac{r(\theta)}{R_{max}}) \]

根据 shading point 的 normal 算出其切线 tangent，算出切线与 view 平面的夹角的 sin 值，同理可算出 \(sin(t(\theta))\)

最终计算 AO 为：

\[\begin{aligned} A(x) & = \frac{1}{2\pi} \int_{\theta = -\pi}^{\pi} (\int^{h(\theta)}_{\phi=t(\theta)} \cos(\phi) \mathrm{d}\phi)W(\theta) \mathrm{d}\theta \\& = \frac{1}{2\pi} \int_{\theta = -\pi}^{\pi} ( \sin(h(\theta))-\sin(t(\theta)))W(\theta) \mathrm{d}\theta \end{aligned} \]

最后对 AO 图像进行一个空间滤波（或者说模糊）来降低噪声

HBAO 的 Normal 问题

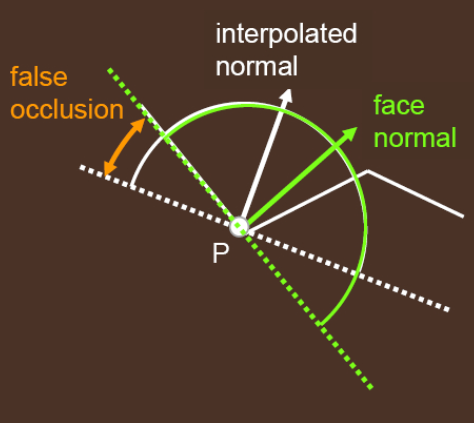
shading point 在利用 normal 计算切线 tangent 的时候，最好使用 face normal（即三角面法线）而非 interpolated normal（通过顶点插值得到的法线）：如果使用 interpolated normal ，那么在模型凹角处容易出现 artifacts。

如下例，face normal 比起 interpolated normal 才更能做到 AO 的正确性：

然而使用 face normal 后，对于低精度（low-tessellation）的曲面来说又会出现 artifacts：可能会出现黑白相间的现象，类似 shadow map 的 shadow acne 现象。

究其原因，如下图假设衔接处的 shading point 本应该是曲面，然而由于使用了低精度的 mesh，由 face normal 计算出来的 tangent plane 是偏下的，因此衔接处的 AO 过度偏暗。

这种情况反而用 interpolated normal 更能做到 AO 的正确性，不过由于大部分情况都不是曲面，因此还是建议算法以 face normal 为核心。

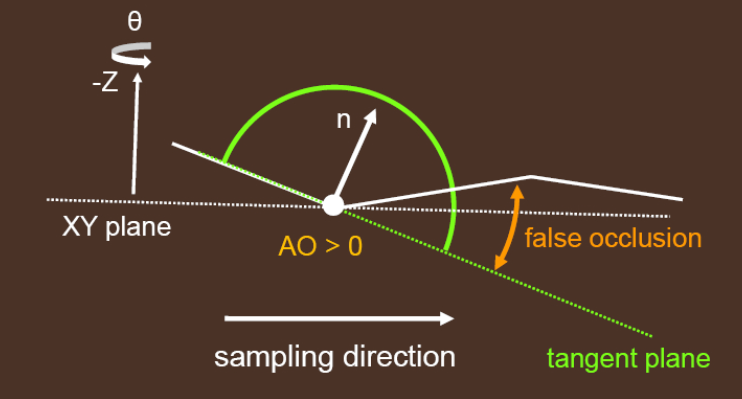
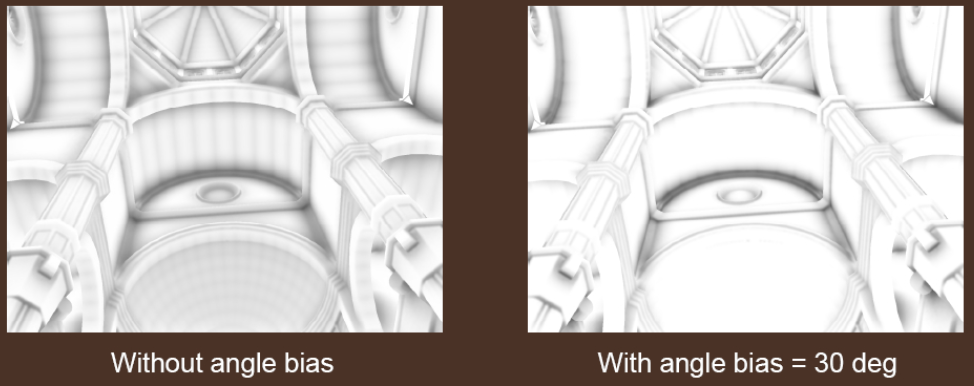
那么干脆借鉴 shadow map bias 的做法，我们也给 HBAO 加 bias（例如可以让 tangent plane 往上抬高 30 度角来）：

HBAO 的采样

HBAO 在选择屏幕空间采样方向和在 ray marching 的时候可以使用开销极其低廉的预定义样本（可通过数组定义）：每帧随机选择一种十字采样方向（共有5种），选定后每个采样方向 ray marching 也只步进两次。

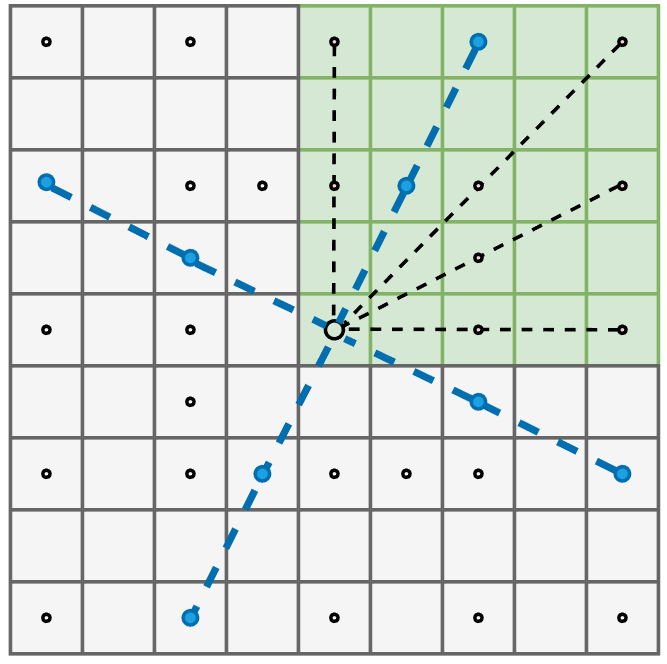
所以这种方式下 HBAO 的样本只需要 4个方向×2个步长 = 8个。其相比于 SSAO，样本数大大减少但却能同时能保持较好质量的 AO。

HBAO 的不连续问题

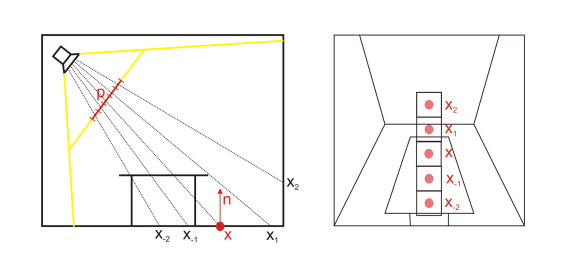
有些情况下，相邻的 shading point 可能 AO 是相差较大导致画面，如下图：

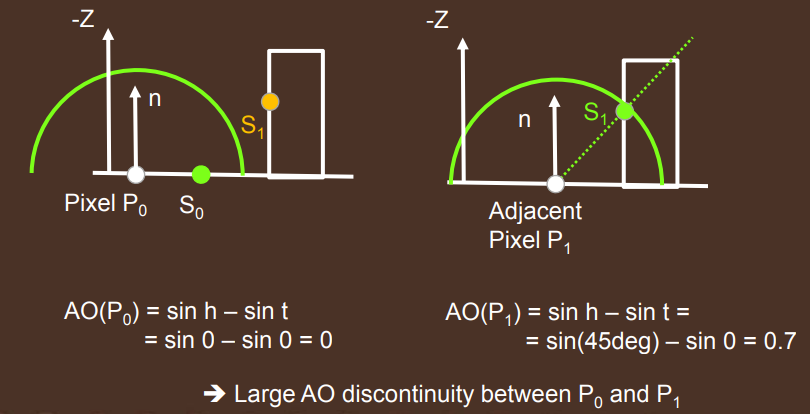
其核心原因在于，\(P_0\) 本来 AO = 0.7，而 \(P_1\) 的遮挡物超出 ray marching 的最远距离，于是 AO 突变为 0。我们当然也可以采用更长距离的 ray marching，代价是要不牺牲性能采样更多样本，要不降低质量使用间隔较大的步长。

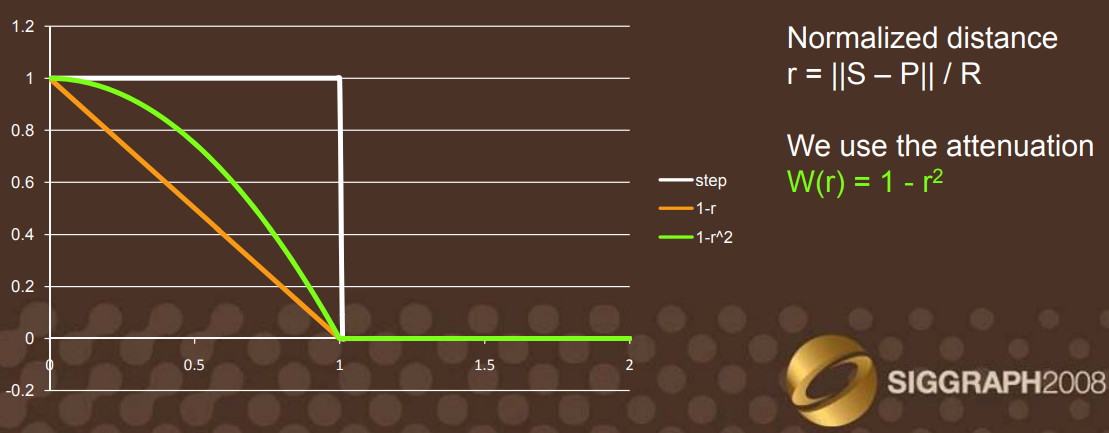
为了减少这种不连续的情况，论文在 HBAO 的流程中引入了混合权重：

\[W(\theta) = max(0,1-\frac{r(\theta)}{R_{max}}) \]

也可以采用更平滑的混合权重：

\[W(\theta) = max(0,1-(\frac{r(\theta)}{R_{max}})^2) \]

虽然总体 AO 会减轻，但是却能够很好地解决不连续问题，并且不引入新的性能开销或者造成 AO 质量降低。

HBAO 的应用与缺陷

应用：

HBAO 比 SSAO 开销往往更低：由于只需要更低于 SSAO 的样本数，甚至还能达到质量更高的 AO 效果。

缺陷：

对于有中空的 AO 情况，HBAO 会把 hit success 的最高仰角以下的方向都认为是被遮挡的，这是与 Ground Truth AO 不符（SSAO 反而更能适应这种中空情形）。

如图左，hit success 的是橙色射线，hit fail 的是绿色射线，而图右的 HBAO 统统认为最高仰角以下的射线都是 hit fail。

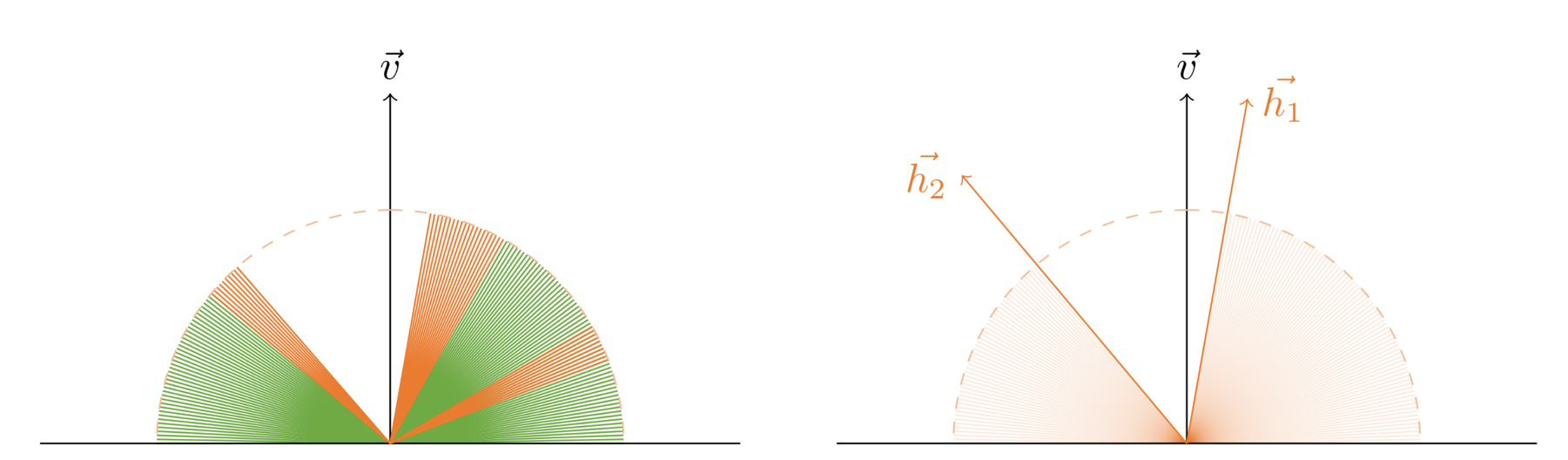
有空再补一补 HBAO+ 和 GTAO 的档

Screen Space Reflection（SSR）/Screen Space Ray Tracing（SSRT）

Screen Space Reflection（SSR）,一类与 ray tracing 思路非常相似的屏幕空间GI方法，因此也有被叫为 Screen Space Ray Tracing（SSRT）。

它的想法是，将屏幕所看到的表面几何信息当成一个场景，然后计算间接光照时，往半球范围若干个方向投射射线，看看能和这个场景的哪个屏幕像素点相交，这些便可以相交的像素点便是提供间接光照的来源。

SSR 需要用到的屏幕信息：color、normal、depth

SSR 的算法流程：

在第一个 pass 只渲染整个场景的直接光照，得到包含直接光照结果的 color buffer 、normal buffer、 depth buffer。
在第二个 pass 对整个屏幕渲染，对于某个 shading point ，在该点往半球随机方向投射若干条射线（使用 ray marching算法），然后将与射线相交的点 \(\mathrm{p'}\) 将对 shading point 的间接光照做出贡献（这与渲染方程是一致的）：

\[L_{\mathrm{indirect}}\left(\mathrm{p}, \omega_{o}\right) = \int_{\Omega^{+},V=1} L_{}\left(\mathrm{p'}, \omega_{i}\right) f_{r}\left(\mathrm{p}, \omega_{i}, \omega_{o}\right) \cos \theta_{i} \mathrm{~d} \omega_{i} \]

其中当射线命中时， \(V = 1\) ；否则，\(V = 0\)

为了减少计算，这里仍然假设次级光源点是 diffuse 的，这样式子实际可以写成：

\[L_{\mathrm{indirect}}\left(\mathrm{p}, \omega_{o}\right) = \int_{\Omega^{+},V=1} \frac{E(\mathrm{p'})}{\pi} f_{r}\left(\mathrm{p}, \omega_{i}, \omega_{o}\right) \cos \theta_{i} \mathrm{~d} \omega_{i} \]

此外，SSR 还可以通过使用不同的 brdf 来实现不同的反射效果：

SSR 效果图：

Ray Marching

得益于带 depth buffer，SSR 可以实现比较廉价的 Ray Marching 效果。Ray Marching 的精度和性能之间的平衡将取决于 march 的步长。

算法先从 start point 开始，

每次往射线方向走一个步长得到一个测试点，将该测试点变换成屏幕坐标 \((u,v,z)\)
根据uv坐标取 depth buffer 对应的深度 \(d\) 与 \(z\) 比较：若 \(z>d\) ，则说明射线碰到该uv位置上像素点的“柱条”，返还该测试点；否则，重复上述步骤

bool RayMarch(vec3 ori, vec3 dir, out vec3 hitPos) {
  float step = 1.0;
  vec3 lastPoint = ori;
  for(int i=0;i<10;++i){
    // 往射线方向走一步得到测试点深度
    vec3 testPoint = lastPoint + step * dir;
    float testDepth = GetDepth(testPoint);
    // 测试点的uv位置对应在depth buffer的深度
    vec2 testScreenUV = GetScreenCoordinate(testPoint);
    float bufferDepth = GetGBufferDepth(testScreenUV);
    // 若测试点深度 > depth buffer深度，则说明光线相交于该测试点位置所在的像素柱条
    if(testDepth-bufferDepth > -1e-6){
      hitPos = testPoint;
      return true;
    }
    // 继续下一次 March
    lastPoint = testPoint;
  }
  return false;
}

Ray Marching + Hi-z

在 SSR 的 ray marching 中，步长短了会导致要走很多步，消耗很多性能；而步长长了则可能会导致越过原本应该相交的地方后面，导致错误的相交。

为了优化这一过程，我们可以对 depth buffer 生成 hi-z（若干层 depth buffer，底层级比高层级的分辨率低），原理类似于 mimap，但不是传统 mimap 所取的平均值，而是换成了取最大值。这样我们在低层级的 depth buffer 进行大步的 marching 时碰到 texel，那么说明可能与在这块 texel 里的某个子像素相交，因此需要降低层级，进行更小步的 marching；若没碰到，则说明不在当前这块 texel 的任何子像素，可以继续下一大步（而且是更激进）。

这个 hi-z 加速方法实际上和 BVH 方法是相似的，hi-z 每个 texel 相当于每个 AABB 包围盒，层级越低则包围盒越大。

mip = 0;
while(level>-1)
    step through current cell;
	if(above Z plane) ++level;
	if(below Z plane) --level;

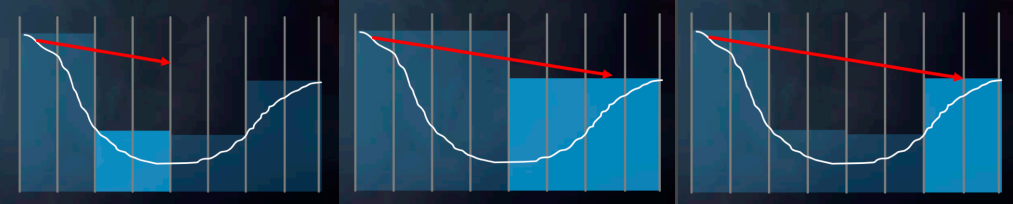
Edge Fading

由于 screen space 的方法天生丢失了屏幕以外的信息，在某些时候的渲染可能会看到反射物比较突兀的断掉了屏幕外的信息：

为了掩盖这一突兀的 artifact，可以使用基于像素uv坐标的间接光照权重贡献，即uv坐标越接近边界（例如接近u=0、u=1、v=0、v=1），则权重贡献应当越小：

优化

BRDF 重要性采样

为了让 SSR 的采样更容易收敛，我们可以根据不同的 BRDF lobe 在进行 importance sampling：

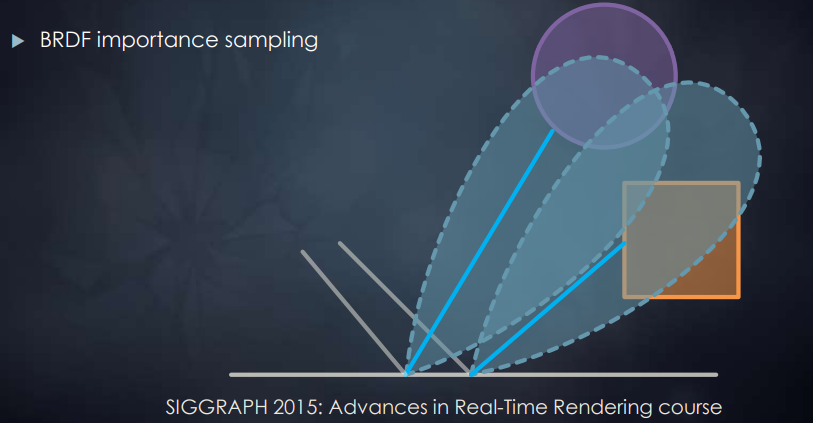
射线结果重用（Radiance Filtering）

当 pixel 的 ray marching 得出一个相交点时，不仅计算出对该 pixel 的间接光照贡献，还可以将计算该点与原 pixel 附近的 pixel 的间接光照贡献并赋给相应的 pixel ：

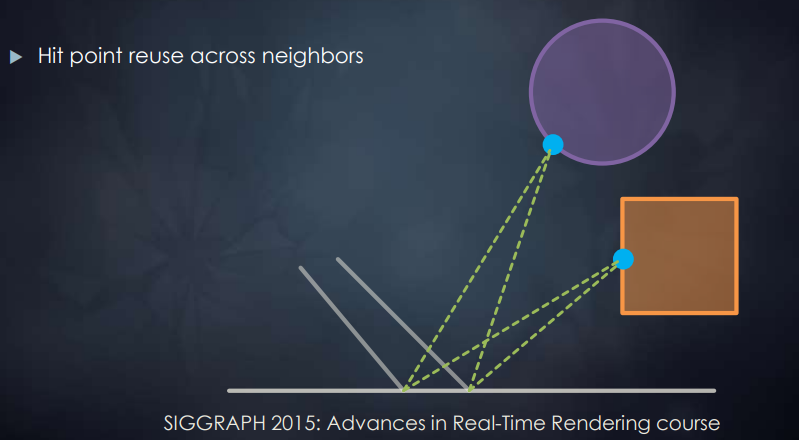
预过滤采样结果

每个方向采样得到的结果将根据不同的 BRDF lobe 来决定这个结果的权重，从而最终综合得到一个过滤后的间接光照结果，减少了采样的 noise 问题：

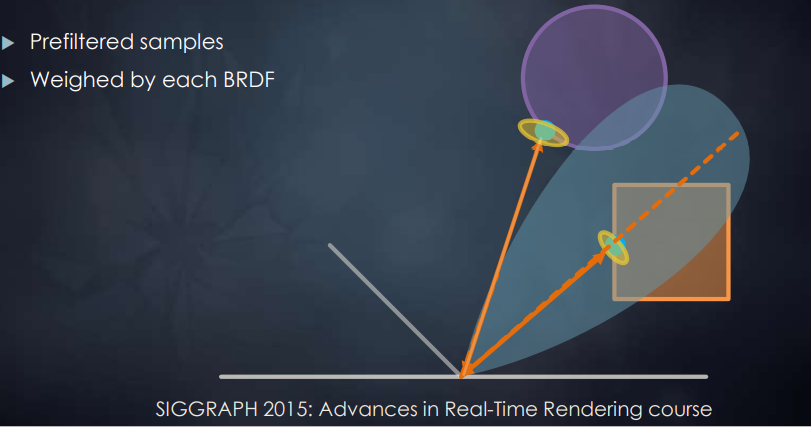
SSR/SSRT 的应用与缺陷

缺陷：

screen space 方法仍然缺失了屏幕所看不到的几何信息

diffuse 情况下，由于要往半球范围均匀采样（不能像specular/glossy那样用importance sampling极大优化采样），容易造成nosiy结果，这时候可能需要牺牲更多的性能来采样更多

应用：

SSR 的渲染效果非常好（更前面的方案看起来总像是增强部分的图像效果）
通过不同的 brdf 函数，可以自由调成各种反射效果（specular/glossy/diffuse）

Screen Space Pixel-projected Reflections

Pixel-projected Reflections（PPR）是用于 planar reflections（平面反射，常见于水面、光滑地板）情况下的一种聪明且低廉的算法，其核心思路是将场景的像素投影到反射平面的像素上，从而避免了从反射平面像素出发投射光线的操作（避免了光追的调用）。

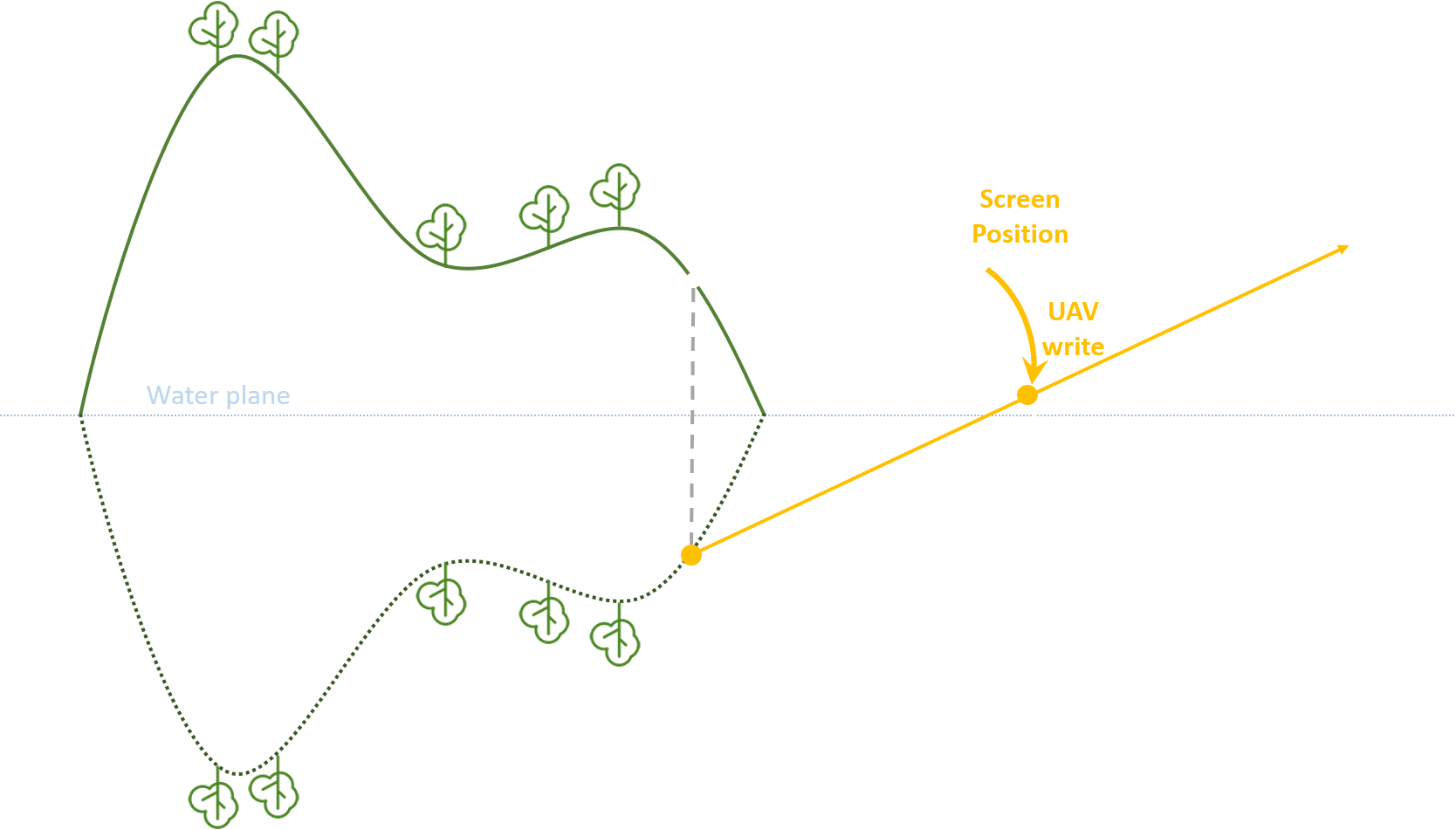
Projection Pass

首先，需要创建一个屏幕大小且元素类型为 uint32 的 intermediate buffer，其将用于存储屏幕位置 offset。场景像素需要根据平面位置和法线来算出对应的目标反射平面像素，并在该目标像素中写入本场景像素的屏幕位置 offset，从而在后续的 reflection pass 中可以让每个反射平面像素找到自己对应的场景像素并获取像素颜色。

具体实现上，在绘制场景物体时和绘制反射平面物体时可采取不同的 stencil flag 写入；随后可以通过一个全屏 PS（开启 stencil test）或者 CS 来完成 projection pass，这样就可以实现对所有场景像素做 projection 操作。

Hash Resolve

在将场景像素投影到反射平面像素时，会存在写入冲突问题：可能会有多个场景像素正好投影到同一个反射平面像素，导致每帧都在随机竞争写入，其错误效果大致如下：

这时候正确的结果应当是只取离反射平面最近的那个场景像素，因为更远的场景像素相当于是被遮蔽了。

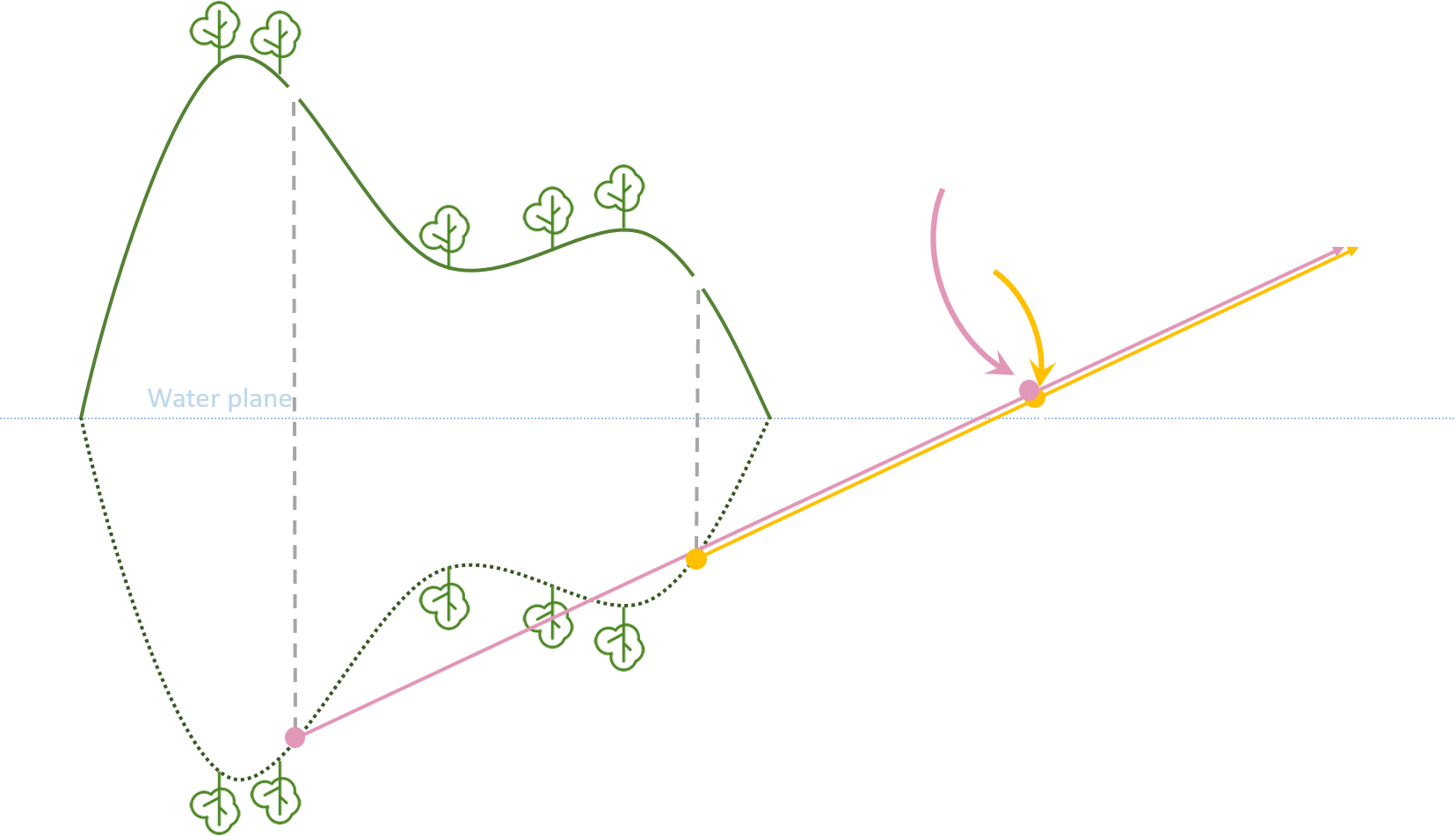
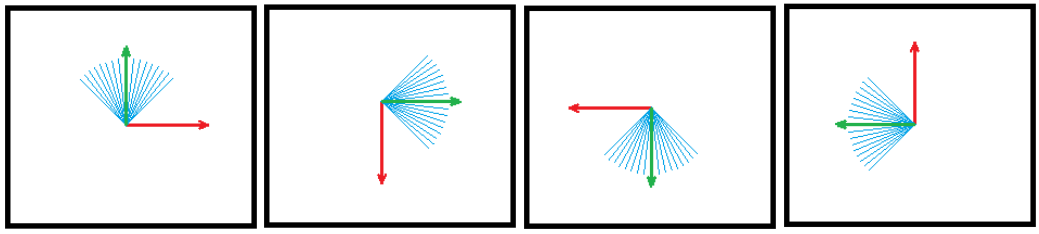
那如何判断哪个场景像素最近？只需要看谁在反射平面法线方向轴上的 offset 最小就取谁，那么可以通过 InterlockedMin 原子操作来解决写入冲突，还能保留正确的写入结果。我们可以对场景像素的位移编码成如下 hash 值：

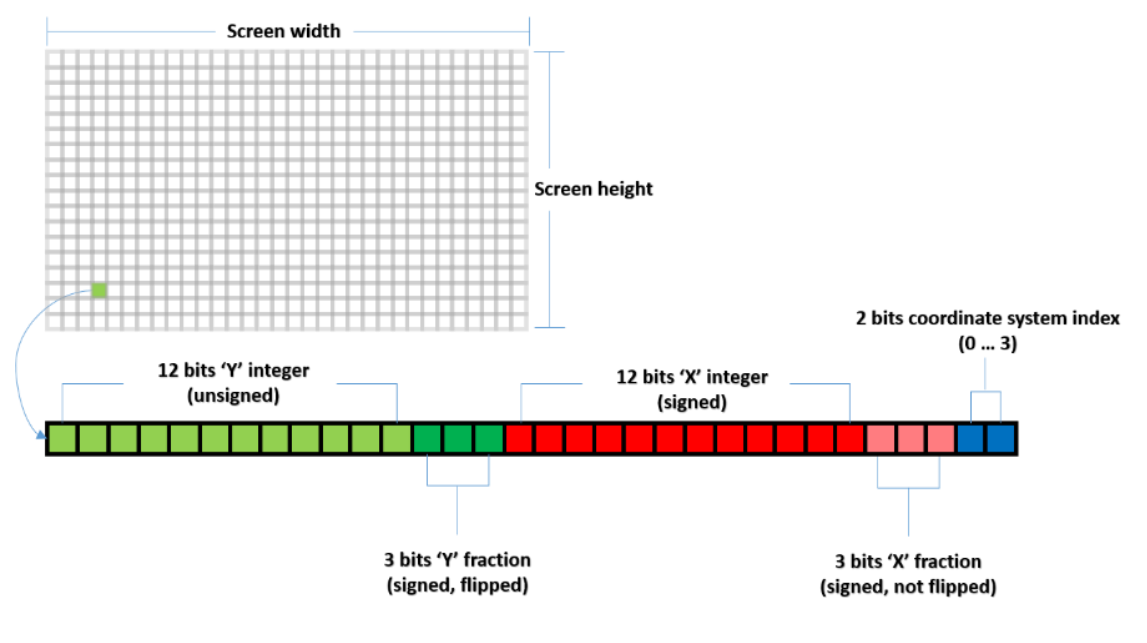
最后两位用于表示如图的 4 种坐标系，从而覆盖了所有反射平面法线方向的情况：法线落在哪个坐标系的蓝色扇形范围，便会使用该坐标系。这样以对应的坐标系为基准，其 y 轴上的值便可以视为 offset。
12位 y 整数值（无符号）和12位 x 整数值（有符号）均为基准坐标系上的 offset。只不过场景像素必定在平面之上，因此 y 值必定不是负数，也就不需要符号位。
3位 y 小数值（有符号），3位 x 小数值（有符号）为补充整数值精度用的，可以在后续步骤中利用到。

对编码后的 hash 值，就可以通过 InterlockedMin 原子操作对 intermediate buffer 进行写入。

uint originalValue = 0;
uint valueToWrite = PPR_EncodeIntermediateBufferValue( offset );
InterlockedMin( uavIntermediateBuffer[ targetPixelIndex ], valueToWrite, originalValue );

Edge Stretch

对于横跨屏幕的平面（尤其常见于水面），由于透视投影的缘故，可能在屏幕边缘处产生反射信息丢失的问题。

Edge fading 可以解决类似问题，而另一种可选的方法是将投影出去的像素往屏幕边缘处拉伸：

可以在写入 intermediate buffer 前，先对投影到的目标像素位置做一个偏移：

float heightStretch = (posWS.z – waterHeight);
float angleStretch = saturate(- cameraDirection.z);
float screenStretch = saturate(abs(reflPosUV.x * 2 - 1) – threshold);
targetPixelPos.x *= 1 + heightStretch * angleStretch * screenStretch * intensity;

Reflection Pass

和 projection pass 恰恰相反，reflection 对所有反射平面像素（而非场景像素）做 reflection 操作：访问 intermediate buffer 上对应的 offset，从而往该 offset 后的屏幕位置获取 scene color。

在具体实现，也需要一个屏幕 PS 或 CS，也同样需要利用 stencil buffer 来保证只对反射平面像素处理。

Holes Filling

然而实际并不是每个反射平面像素都被写入过 offset，总是会出现 holes，主要有两类情况：

反射平面像素对应的 projection 位置虽然存在场景像素，但是刚好该场景像素投影到了隔壁的反射平面像素，擦边而过了；往往呈现出黑色点状或线状。
反射平面像素对应的 projection 位置不存在正确的场景像素（屏幕信息不能表达完整的场景信息）；往往呈现出大块黑色。

第一类问题可以通过复用邻近 4 个平面像素的 offset 来解决。具体就是在 intermediate buffer 中读取周围 4 个 pixel 的 offset，看哪个 offset 离自己最近就当成自己的 offset，这时候 hash 值中的小数部分就能派上用场了（如果仅看整数部分大概率 4 个 offset 都会一样近）。

uint v0 = srvIntermediateBuffer[ vpos.x + vpos.y * int(globalConstants.resolution.x) ];
// read neighbors 'intermediate buffer' data
const int2 holeOffset1 = int2( 1, 0 );
const int2 holeOffset2 = int2( 0, 1 );
const int2 holeOffset3 = int2( 1, 1 );
const int2 holeOffset4 = int2(-1, 0 );
const uint v1 = srvIntermediateBuffer[ (vpos.x + holeOffset1.x) + (vpos.y + holeOffset1.y) * int(globalConstants.resolution.x) ];
const uint v2 = srvIntermediateBuffer[ (vpos.x + holeOffset2.x) + (vpos.y + holeOffset2.y) * int(globalConstants.resolution.x) ];
const uint v3 = srvIntermediateBuffer[ (vpos.x + holeOffset3.x) + (vpos.y + holeOffset3.y) * int(globalConstants.resolution.x) ];
const uint v4 = srvIntermediateBuffer[ (vpos.x + holeOffset4.x) + (vpos.y + holeOffset4.y) * int(globalConstants.resolution.x) ];
// get neighbor closest reflection distance
const uint minv = min( min( min( v0, v1 ), min( v2, v3 ) ), v4 );

第二类问题则比较难解决，将留到后面的优化部分。

优化

Fallback 成其它 Ray Tracing 方法

为了解决第二类 holes filling 问题，可以对 holes filling 后仍然缺失 offset 信息的反射平面像素所在的 tile 进行标记；接着，用额外一个 CS pass 来对这些被标记 tiles 的 pixels 进行 radiance 的计算（例如使用 SSRT 或 reflection probe 采样）。

Glossy Reflection & Normal Map

对于 PPR 技术来说，一个平面反射像素就只有唯一一个镜面反射方向的样本，也因此只适合做 mirror reflection（镜面反射）。然而只要扩展一下，也还是可以为平面反射引入 glossy reflection，甚至应用上 normal map 来让每个平面反射像素都有不同的法线。首先，我们需要根据 normap map 算出平面反射像素的法线后，再根据 BRDF importance sampling 来生成一个 ray。

在 SIGGRAPH 2017 Optimized pixel-projected reflections for planar reflectors 的做法中，这个 ray 将使用 SSRT 来获取 radiance，如果 SSRT miss 了才使用 mirror reflection 的结果。然而这种做法实际上和 SSR 没太大区别。

虽然 mirror ray 和 generated ray 的射线方向往往不是同的，但是它们依然比较相似。那么我们为什么不充分利用 mirror ray 信息来指导 generated ray 呢？因此一个思路是牛顿迭代法：

将 mirror ray 的长度 scale 一下 generated ray 得到一个预测点。
摄像机往预测点看，访问对应的 depth，重建出 p'' 的世界坐标，并同时计算 p'' 与平面反射像素的距离，并再次用该距离 scale 一下 generated ray 得到下一个预测点（进行了一次迭代）。
摄像机往第二个预测点看，访问对应的 color 作为本次 generated ray 的 radiance 结果返回。

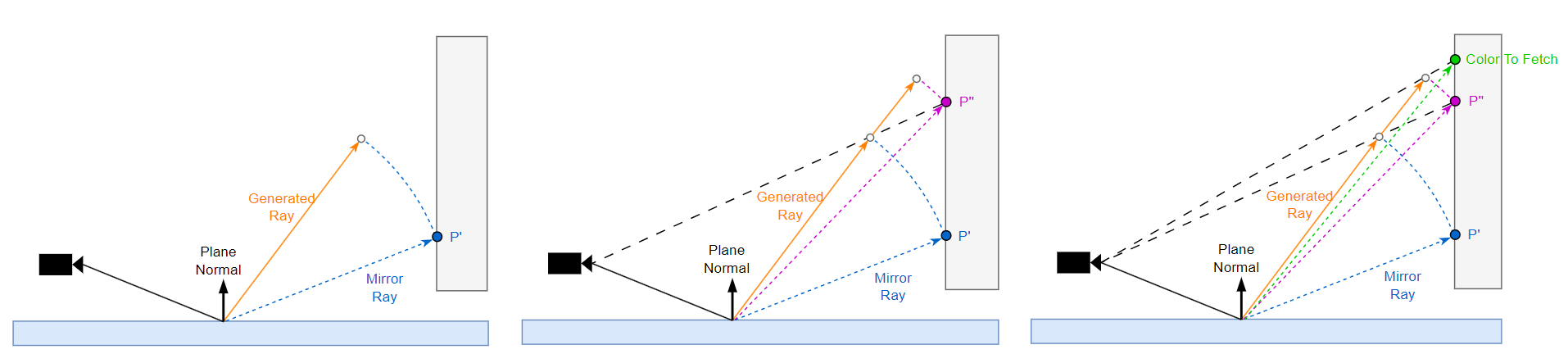
也就是说，如果需要追求更高的精度，可以通过 n 次访问 depth buffer，来获取 n + 1 次的迭代效果，并且迭代的初始值为 mirror ray 的长度，已经算是一种非常接近真实解了（取决于 mirror ray 和 generated ray 的相似度）。

当然牛顿迭代法在表面连续的情况下能够完美工作，在突变的地方可能有一定效果问题，但是整体效果仍然是可接受的。

PPR 的应用与缺陷

在传统 planar reflections 中，需要把场景多绘制一遍到反射平面上。而 PPR 只需要利用屏幕信息，就可以实现 planar reflections 的效果，无需额外多一次绘制场景；当然 PPR 仍然会存在屏幕信息不完整的问题，需要通过 edge fading 等方法减轻边缘信息丢失问题。
PPR 与 SSR 利用屏幕信息的思路是相似的，然而在实现的思路上却是相反的；区别在于 PPR 是从场景像素传播到反射平面像素的（data scattering），而 SSR 是反射平面像素从场景像素中获取颜色的（data fetching）。在性能上，PPR 往往比 SSR 更加开销低廉，因为避免了需要很多步采样深度图的 ray marching。只是 PPR 的使用场景只适合用于水平的反射平面上（如平地板、水面），而不能用于形状复杂的任意表面上。

参考

posted @ 2021-10-31 21:12 KillerAery 阅读(5558) 评论(1) 收藏举报

刷新页面返回顶部

KillerAery