基于预计算的实时环境光照（Real-time Environment Lighting Based On Precomputation）
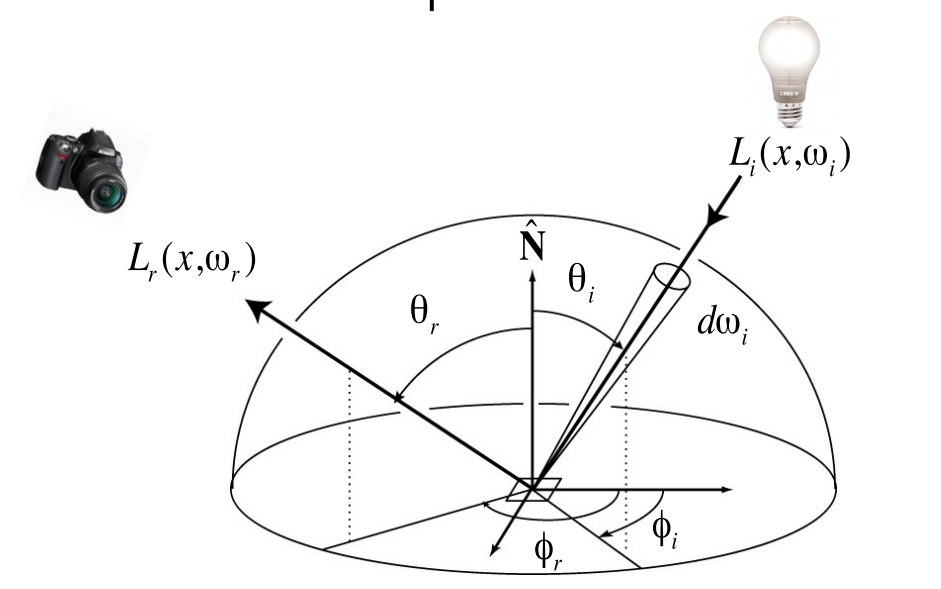
环境光照（Environment Lighting）：用于大型、复杂但强度较小的光源，包括天空光（Sky Light）和云散射的光、从场景中的超大型物体反弹的间接光照以及超大型 area light 的直接光照（往往是能包围整个场景的无限远的 area light）。这种光源具有物体位置无关的特性，即物体无论位于场景的哪里，所接受到的环境光照都是一样的（不考虑辐射度传输因素，例如几何相关的 visibility）。
其中，Ambient Light 是最简单的环境光照，相当于给整个场景所有物体提升同样的亮度（同一颜色）。
因为环境光往往是超大型的，而场景中物体相隔不远的情况下，就可以假设场景所有物体所受到的环境光是一样的，例如相隔一条街的物体能受到的天空光照几乎是一样的。当然考虑光的辐射度传输因素的话，不同物体所受到的环境光照将有所不同，但我们可以将其拆解成环境光信息和辐射度传输信息，环境光信息依然可以全场景共享，而辐射度传输信息可以每个物体各有一份。
基于图像的光照（Image Based Lighting，IBL）
基于图像的光照（Image Based Lighting，IBL），简单的说就是一类通过 环境贴图（Environment Map） 来保存环境光信息，从而实现基于物理的渲染方法。
为了表示来自四面八方的环境光信息，IBL 使用 Spherical Map 或者 Cube Map 的方式来存储：
IBL 可用于 diffuse/glossy/specular 物体（基本上包含大部分物体了）渲染：这取决于环境贴图，环境贴图分辨率越大，那么所能表示高频信息就越多，从而越适合 specular 物体的渲染；而分辨率越低，所表示的信息更多是低频信息， 则 diffuse 物体的渲染也足以满足，而且还能节省一定存储空间。
The Split Sum Approximation
IBL 中最常见的算法便是基于 The Split Sum Approximation 的算法。
我们知道，一般的渲染方程如下：
在实际渲染的时候，我们当然可以使用蒙特卡洛方法实现该渲染方程，然而这样的开销是巨大的（每个shading point都要做多重采样，而且结果很容易是noisy的）。
为了进一步加快式子，这里有一个很经典的近似公式：
积分域 \(\Omega_G\) ：在原本 \(\Omega^+\) 的积分域范围内剔除掉 \(g(x) = 0\) 的地方而剩余的范围。
想让这个公式近似效果比较精确，那么需要满足以下一种或两种条件：
- 积分域 \(\Omega_G\) 比较小
- \(g(x)\) 比较光滑，即变化不是很大
而我们的观察是：
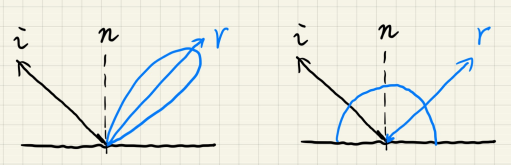
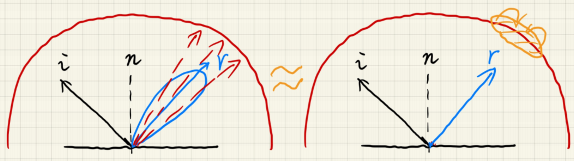
- 如果 BRDF 是 glossy/specular 的，那么它的 lobe 往往是花瓣状，即只有很小的积分域才能接受环境光。
- 如果 BRDF 是 diffuse 的，那么它的 lobe 往往是均匀的半球状，即无论哪个方向的环境光打进来， \(f_r\) 函数的输出几乎没多少变化（甚至是个常数）。
于是基于以上理论，Split Sum 方法对渲染方程改造成这样的近似公式来获得渲染的加速：
对渲染方程拆分成两个部分（环境光积分、BRDF积分）后就可以通过预计算的方式（后面两节会介绍如何预计算）分别减少这些积分的运行时开销，总结这种方法的好处是：
- Split Sum 方法和原始蒙特卡洛方法的图像效果几乎一模一样
- 由于不用对环境贴图进行多重采样，性能开销大大减低了
预过滤环境贴图
环境光积分：
因为我们已经拥有一张环境贴图（无论是实时的还是预渲染的）来存储环境光信息了，为了计算环境光部分的积分，需要在 \(\Omega_{fr}\) 范围内做多次光线采样。但是，可以有一个几乎等价但避免运行时多次采样的方式：
预先对纹理进行滤波操作（模糊），我们只需要对滤波后的环境贴图采样一次光线方向就能得到积分。
滤波后的环境贴图实际上称为 Irradiance Environment Map ：原来环境贴图中的单位是 radiance \(L(\mathrm{x}, \omega)\)，贴图积分后的单位则变成了 Irradiance \(E(x)\)。
当然，BRDF Lobe 的形状越尖锐，即环境光积分范围越小，就需要使用模糊程度更低的环境贴图；反之 BRDF Lobe 的形状越粗壮，即环境光积分范围越大，就需要使用模糊程度更高的环境贴图。
我们可以使用 Mipmap技术 来生成不同Level的环境贴图，通过三线性插值（Trilinear Interportion）的方式来得出任何模糊程度且任何2D位置的环境光滤波结果。
IBL 往往用于支持静态环境光照，这样就可以进行预过滤环境贴图；当然也可以支持动态环境光照，只是需要实时过滤出动态的环境贴图，有一定的开销。
预计算 BRDF 积分
回顾 Microfacet BRDF 的组成：
- Fresnel项（举例 Schlick's approximation）
- NDF项（举例 Beckmann NDF）
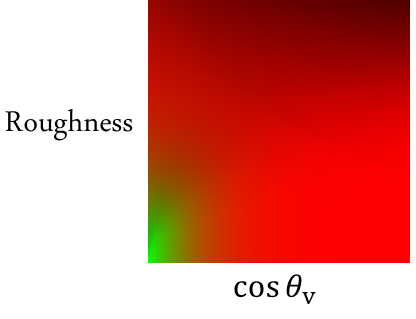
可以预想到，该BRDF 的积分结果依赖于三个参数：
- \(F_0\)（Fresnel项系数）
- \(\alpha\) （粗糙度 roughness）
- \(\theta_v\) （反射方向与法线的夹角，实际上决定了 \(\theta_{vh}\)、\(\theta_{h}\)）
我们可以把 \(F_0\) 项拆出来，让BRDF 积分拆成两个积分，但是这些积分都减少了一个依赖的参数：
这样，对于相同的材质（相同的BRDF），我们就可以针对剩余两个依赖的参数 \(\alpha\) 、\(\theta_v\) 建立一张 二维查询表，其两个通道分别代表 A 与 B 的值：
SH（Spherical Harmonics，球谐）
SH 是 PRT 的前置知识，单独提出来讲一下。
对于任意函数 \(f(x)\) ，不管是连续的还是不连续的，我们可以展开成一系列基函数（每项都带某个系数）的线性组合：
例如，多项式展开可以看成是一系列基函数（多项式）的线性组合：\(f(x)=c_{0} +c_1\cdot x^1 + c_2 \cdot x^2 + ...\)
再例如，傅立叶变换也可以将 \(f(x)\) 表示成另一系列基函数（各种频率的正弦谐波）的线性组合：
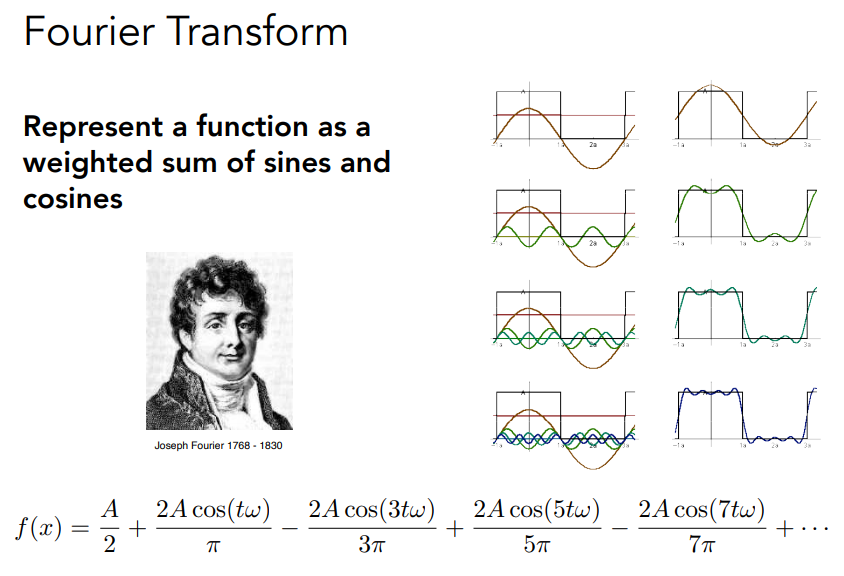
而 球谐（Spherical Harmonics，SH） 便是定义在球面上的一系列2D基函数，它与2D傅里叶序列有点相似，但非常适合球面函数 \(f(\omega)\)（即参数为单位球面向量）。
SH 是分阶数的：
- 在第0阶（l=0）有1个基函数（m=0）
- 在第1阶（l=1）有3个基函数（m=-1,0,1）
- ...
- 在第n阶（l=n）有2n+1个基函数（m=-n,...,0,...,n）。
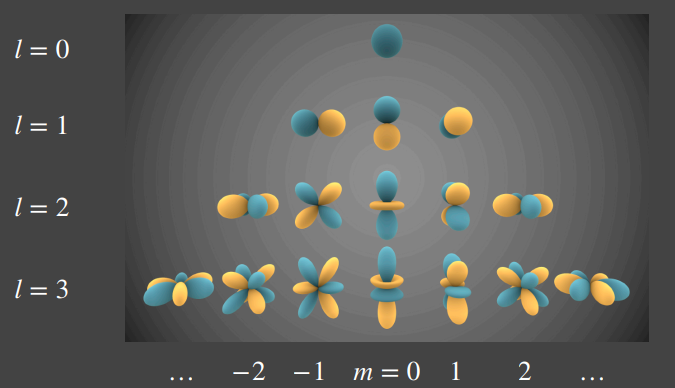
图中蓝色意味着正值，黄色意味着负值。
实际上，阶数越低的基函数所代表的信息就越是低频。如果要完全复原一个任意函数，我们需要无穷阶的 SH，而如果我们只要复原一个任意函数的近似（换句话说只重建出该函数的低频信息），那么我们完全可以只需要前几阶的 SH（包含 l=0,l=1,...,l=n 每一阶的所有基函数）去拟合。
实时渲染中常用二阶SH（其包含系数总共为1+3=4个）和三阶SH（其包含系数总共为1+3+5=9个）来表示。
SH 基函数的形式比较复杂，只建议看一眼就跳过。
SH 的实数形式的基函数如下：
\[y_{l}^{m}(\theta, \varphi)=\left\{\begin{array}{rl}\sqrt{2} \operatorname{Re}\left(Y_{l}^{m}\right) & m>0 \\ \sqrt{2} \operatorname{Im}\left(Y_{l}^{m}\right) & m<0 \\ Y_{l}^{0} & m=0\end{array}=\left\{\begin{array}{cc}\sqrt{2} K_{l}^{m} \cos m \varphi P_{l}^{m}(\cos \theta) & m>0 \\ \sqrt{2} K_{l}^{m} \sin |m| \varphi P_{l}^{|m|}(\cos \theta) & m<0 \\ K_{l}^{0} P_{l}^{0}(\cos \theta) & m=0\end{array}\right.\right. \]其中，
\(K_{l}^{m}=\sqrt{\frac{(2 l+1)(l-|m|) !}{4 \pi(l+|m|) !}}\)
\(p^m_l\) 为勒让德多项式（Legendre polynomials）：
- $P_0^0= 1 $
- $P_{m}^{m} =(1-2 m) P_{m-1}^{m-1} $
- $P_{m+1}^{m} =(2 m+1) z P_{m}^{m} $
- $ P_{l}^{m} =\frac{(2 l-1) z P_{l-1}^{m}-(l+m-1) P_{l-2}^{m}}{l-m} $
z为球面向量对应球面坐标的z值，该多项式不依赖x值y值。
以下是前3阶的SH实数形式的基函数：
\(l=0\)：
\[Y_{00}=s=Y_{0}^{0}=\frac{1}{2} \sqrt{\frac{1}{\pi}} \]\(l=1\)：
\[\begin{aligned} Y_{1,-1}&=p_{y}=i \sqrt{\frac{1}{2}}\left(Y_{1}^{-1}+Y_{1}^{1}\right)=\sqrt{\frac{3}{4 \pi}} \cdot \frac{y}{r} \\Y_{1,0}&=p_{z}=Y_{1}^{0}=\sqrt{\frac{3}{4 \pi}} \cdot \frac{z}{r} \\Y_{1,1}&=p_{x}=\sqrt{\frac{1}{2}}\left(Y_{1}^{-1}-Y_{1}^{1}\right)=\sqrt{\frac{3}{4 \pi}} \cdot \frac{x}{r} \end{aligned} \]\(l=2\)：
\[\begin{aligned} Y_{2,-2}&=d_{x y}=i \sqrt{\frac{1}{2}}\left(Y_{2}^{-2}-Y_{2}^{2}\right)=\frac{1}{2} \sqrt{\frac{15}{\pi}} \cdot \frac{x y}{r^{2}} \\Y_{2,-1}&=d_{y z}=i \sqrt{\frac{1}{2}}\left(Y_{2}^{-1}+Y_{2}^{1}\right)=\frac{1}{2} \sqrt{\frac{15}{\pi}} \cdot \frac{y z}{r^{2}} \\Y_{2,0}&=d_{z^{2}}=Y_{2}^{0}=\frac{1}{4} \sqrt{\frac{5}{\pi}} \cdot \frac{-x^{2}-y^{2}+2 z^{2}}{r^{2}} \\Y_{2,1}&=d_{s z}=\sqrt{\frac{1}{2}}\left(Y_{2}^{-1}-Y_{2}^{1}\right)=\frac{1}{2} \sqrt{\frac{15}{\pi}} \cdot \frac{z x}{r^{2}} \\Y_{2,2}&=d_{x^{2}-y^{2}}=\sqrt{\frac{1}{2}}\left(Y_{2}^{-2}+Y_{2}^{2}\right)=\frac{1}{4} \sqrt{\frac{15}{\pi}} \cdot \frac{x^{2}-y^{2}}{r^{2}} \end{aligned} \]
SH 与一般的基函数相比，具有以下性质：
- 基函数之间具有正交性（orthonormal）
- 通过 投影（Projection） 可以很方便得到 SH 系数（SH coefficients）
- 通过系数向量组与基函数组的点积（前n阶的基函数/系数共有 n*n 个）可以很方便重建球面函数
- product projection：\(c(\omega)=a(\omega)b(\omega)\) ，已知 \(a\) 的形式而 \(b\) 未知，有
其中，\(\vec{c}\) 为 \(c(\omega)\) 的SH系数向量组，\(\vec{b}\) 为 \(b(\omega)\) 的SH系数向量组，\(M\) 为 \(n^2\) X \(n^2\) 的矩阵，其元素为
这样我们就可以预计算好 \(M\) ，等到知道 \(\vec{b}\) 后，乘起来就能得到 \(\vec{c}\)
推导：\(令 M_{i}(\omega)=a(\omega)B_i(\omega)\)
\[\begin{align} c_i &= \int_{\Omega} a(\omega)b(\omega)B_i(\omega) d\omega \\ &= \int_{\Omega} M_i(\omega)b(\omega)d\omega \\ &= \int_{\Omega} \sum_{j=1}^{n^2} (M_{ij} B_j(\omega)) b(\omega) d \omega \\ &= \sum_{i=1}^{n^2} M_{ij} \int_{\Omega} B_j(\omega)b(\omega) d \omega \\ &= \sum_{j=1}^{n^2} M_{ij}\cdot b_j \end{align} \]
-
支持插值，对 SH 系数的插值相当于对重建的函数值的插值。
-
旋转不变性（rotational invariance），对函数 \(f\) 的旋转 \(R_{SH}\) 等价于对 \(f(\omega)\) 的自变量的旋转 \(R_{3D}\)：
预计算辐射度传输（Precomputed Radiance Transfer，PRT）
预计算辐射度传输（Precomputed Radiance Transfer，PRT） 是一类基于预计算 radiance transfer（辐射度传输）的渲染方法。
注：PRT 核心并不是预计算环境光照，而是预计算辐射度传输。
所谓 radiance transfer，可以理解成是一种关于光路传输分布的几何信息，例如 shadow，ambient occlusion，物体表面互反射等效果都属于此。也就是说 PRT 要求几何信息是静态的，如果应用到物体上，就需要物体本身不会发生形变；如果应用到几何场景上，就需要场景的几何不会发生变化。
PRT 方法在 2002年 SIGGRAPH 会议被 Peter-Pike Sloan 首先提出，并从此掀起了一波 PRT 方法的研究浪潮，当时论文所实现的 PRT 算法便是大量运用了球谐（SH）方式。实际上 PRT 不仅可以通过 SH 去表示光路传输分布，还可以有其它方式去表示（如 Spherical Gaussian、Wavelet）。
PRT（SH lighting & SH transfer）效果（分别为 diffuse 物体的无阴影情况、diffuse 物体的阴影&互反射情况、glossy 物体的无阴影情况、glossy 物体的阴影&互反射情况。）：
可以看到 PRT 其实不像 IBL 直接应用环境光照，而是额外考虑了物体几何对环境光照的遮蔽效果。
PRT 首先将渲染方程分为两个球面函数，即环境光部分（lighting function）和传输部分（transfer function）：
SH Lighting
由于环境光是场景所有物体共享的，所以往往只需要存储一份全局信息，我们甚至可以使用 IBL 方法，但是在 PRT 采用了一种更加压缩的环境光照表达方式，即 SH Lighting。
球谐光照（SH Lighting）：使用低阶的 SH 来表示环境光照，这样只需要预先存储少数个 SH 系数（diffuse 情况下 2 阶SH Lighting 只需 RGB 每个通道各 4 个系数，即共 12 个系数）就可以重建出环境光照。
传统的环境光照信息往往使用环境贴图（Environment Map）表示，这往往需要一个庞大的二维数组存储各个 texel 的值，十分耗费空间，而且采样和纹理I/O也有一定开销。而纹理本质上也是一个函数（信号），输入二维坐标，输出对应纹素的 RGBA 值，因此可以用 SH 表示。
- SH Lighting 只预先存储若干个 SH 系数，而不必存储一整张环境贴图，大大减少存储空间和 I/O 开销。
- SH 所能表示的 lighting 信息是低频的，因此 SH lighting 只适用于 diffuse 和 glossy 的物体而不适用于 specular 的物体。
- 环境光照动态性会有所限制（最多只能支持环境光照的 rotation）。
SH Radiance Transfer
传输部分则因为是几何相关的，即每个位置的 transfer 信息往往是不一样的，为此可以每个顶点存储一份 transfer 信息，PRT 同样使用了 SH 来表达 transfer 信息。
PRT 中每个顶点预先存储若干个 SH 系数（diffuse情况下）或者矩阵（glossy情况下），而顶点之间的位置则通过插值的方式来得到对应的 transfer 信息。
- 预计算 radiance transfer 可以在实时渲染中以极低代价实现单个物体的自阴影、互反射的局部几何传输效果。
- 物体自身不能有局部的几何变化（但可以整体 scale, rotation 和 transition）。
如果要将 PRT 应用到场景中，则就要求场景所有物体不能发生任何几何变化（包括 scale，rotation，transition）。由于场景的几何复杂度往往比单个物体的几何复杂度要高得多，并且渲染效果也明显的多，因此要求的 SH 阶数应当更高（精度更高），导致更沉重的空间需求，所以下文以单个物体的 PRT 方法为例讲解。
预计算 SH Lighting & Transfer
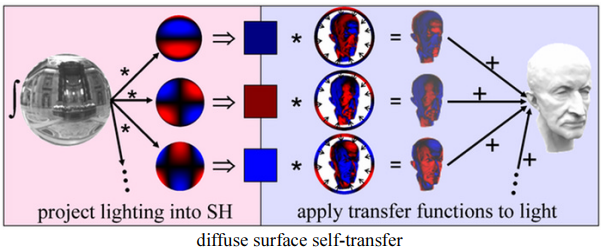
Diffuse 物体
Diffuse 物体的渲染方程：
\(L_e\) 代表环境光； \(\rho\) 为 BRDF 项；\(V\) 为 Visibility，表示不被遮挡的程度，往往表现为自遮挡产生的阴影现象。
- 由于物体是 diffuse 的，因此它的 BRDF 将是一个常数 \(\rho\) （无论从哪个方向观察都得到相同的BRDF值），也因此 diffuse 物体的 \(L\) 将是一个常量值，而不受参数 \(r\) 影响
- 对于 lighting 部分 \(L(\mathbf{\omega})\)，原本需要对 Environment Map 进行查询，而现在可以换成使用 SH 函数去表示：\(L_e(\mathbf{\omega}) \approx \sum l_{i} B_{i}(\mathbf{\omega})\)
- 对于 transfer function 部分 \(T(\omega)=V(\mathbf{\omega}) \max (0, n\cdot \mathbf{\omega})\) ， 也可以换成使用 SH 函数去表示：\(T(\omega) \approx \sum T_j B_j(\omega)\)
代入渲染方程整理后得：
这样，我们只需要预计算出 \(l_i\) 和 \(T_i\)，就能让运行时的diffuse物体渲染速度大大提升。
预计算过程：
-
对整个环境光信息（环境贴图），预计算 lighting 的 SH 系数向量组 \(\vec{l}\)，其中一个元素为：\(l_{i}=\int_{\Omega^+} L_e(\mathbf{\omega}) B_{i}(\mathbf{\omega}) \mathrm{d} \mathbf{\omega}\)
-
对每个顶点，预计算 light transfer 的 SH 系数向量组 \(\vec{T}\)，其中一个元素为：\(T_i=\int_{\Omega^{+}}V(\mathbf{\omega}) \max (0, n\cdot \mathbf{\omega}) \mathrm{B}_{i}(\mathbf{\omega}) \mathrm{d} \mathbf{\omega}\)
此时，我们可以理解成系数 \(l_i\) 代表了环境光照（lighting）的信息，而系数 \(T_i\) 代表了在某个顶点上光路传输（light transfer）的信息；整个模型预计算完成之后将会得到一个 lighting 系数向量和模型顶点数量对应的 transfer 系数向量。
运行时渲染过程：
-
在 vertex shading 阶段计算顶点的 SH 颜色 \(L(r) \approx \rho \sum_{i=1}^{n^2} l_{i} T_{i} = \rho( \vec{l}\cdot \vec{T})\)
-
在 pixel/fragment shading 阶段得到插值后的 SH 颜色即为该像素的颜色
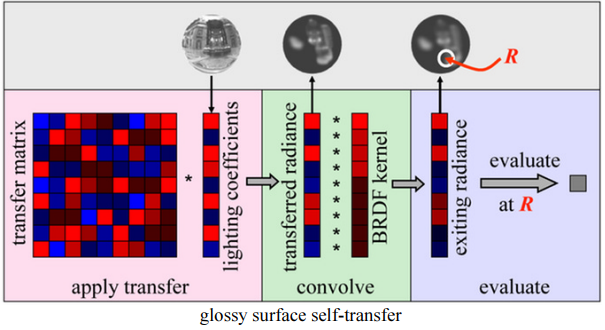
Glossy 物体
Glossy 物体的渲染方程：
对于 glossy 物体，不同视角观察物体表面同一点会有不同的光照。因此 glossy 的 BRDF 将是四维的函数（参数不仅包含\(\mathbf{\omega}\)，还包含\(r\)），这次将 BRDF 算入 transfer，则 transfer function 将额外增加一个二维参数 \(r\)
-
对于环境光（lighting）即 \(L(\mathbf{\omega})\)，原本需要对 Environment Map 进行查询，而现在可以换成使用 SH 函数去表示：
\[L_e(\mathbf{\omega}) \approx \sum l_{i} B_{i}(\mathbf{\omega}) \] -
对于传输函数（transfer function） \(T(r,\omega)=\rho(r,\mathbf{\omega}) V(\mathbf{\omega}) \max (0, n\cdot \mathbf{\omega})\) ，换成使用 SH 函数去表示：
\[T(r,\omega) \approx \sum_{i=1}^{n^2} T_{i}(r)B_i(\omega)\approx \sum_{i=1}^{n^2} \sum_{j=1}^{n^2} T_{ij} B_j(r)B_i(\omega) \]
由于额外多了一个二维的参数，transfer 系数将是一个矩阵而非之前 diffuse 情况下的系数向量
代入渲染方程整理后得：
预计算过程：
- 对整个环境光信息，预计算 lighting 的 SH 系数向量组 \(\vec{l}\)，其中一个元素为：\(l_{i}=\int_{\Omega^+} L(\mathbf{\omega}) B_{i}(\mathbf{\omega}) \mathrm{d} \mathbf{\omega}\)
- 对每个顶点，预计算 light transfer 矩阵 \(T\)，其中一个元素为：\(T_{ij}=\int_{\Omega^{+}}\mathrm{B}_{j}(\mathbf{\omega}) T_i(\omega) \mathrm{d} \mathbf{\omega}\) 、\(T_i(r) = \int_{\Omega^+}T(r,\omega)B_i(\omega)d\omega\)
由于 Glossy 物体需要每个顶点存储三个矩阵 T（RGB颜色每个通道对应1个矩阵），这使得空间开销略大，因此不太实用。
运行时渲染过程：
- 在 vertex shding 阶段计算顶点的 SH 颜色 \(L(r) \approx \sum_{i=1}^{n^2}\sum_{j=1}^{n^2} l_{i} T_{ij} B_j(r) = T\vec{l}\cdot \vec{B(r)}\)
- 在 pixel/fragment shading 阶段得到插值后的 SH 颜色即为该像素的颜色
原论文实际上还有个 BRDF 卷积步骤。但是本身用SH表示环境光信息已经足够低频（模糊）了，对这个卷积步骤，个人先存个疑。
预计算 Interreflection Transfer
而前面的渲染方程中：
只考虑几何传播关系的因素只有 \(V(\omega)\cdot max(0,n\cdot\omega)\)，即只可实现阴影或者无阴影（令 \(V=1\)）的效果，并不能实现互反射（interreflection）的效果。
所谓 interreflection，实际上就是某个点朝外围环境看时，\(V=0\) 意味着有几何部分遮挡住了直接的环境光，但实际上遮挡还意味着这些几何部分上的出射光会反射给该点，这就形成了该点间接的环境光照。
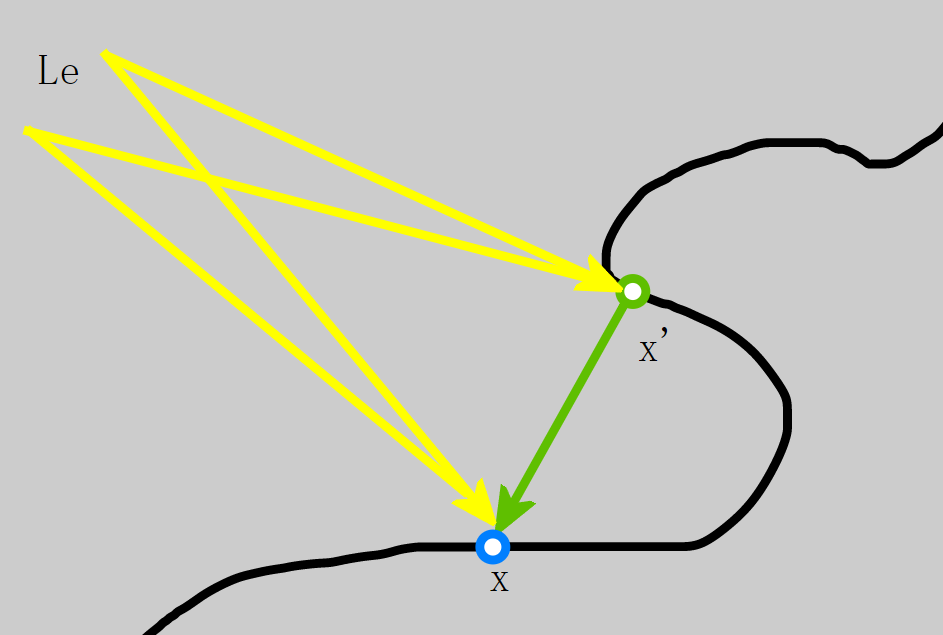
（迭代）增加 1 次互反射的渲染方程：
\(L^n_x\) 意味着在某个点 \(x\) 的 radiance，而 \(x'\) 则是从 \(x\) 朝 \(\omega\) 方向进行 raycast 而得到相交的其它点（\(x'\) 依赖于 \(\omega\)），而 \(n\) 则代表了迭代了多少次。
Diffuse 物体
由于 diffuse 与出射方向无关，因此去掉 \(L\) 的参数 \(\omega\)。
将上述式子左右两边同时分离出 \(\vec{l}\) （因为无论点在 \(x\) 还是别的 \(x'\)，其所在的环境光照 lighting SH 系数都是一样的 ），则意味着我们实现 Interreflection 的效果只需要在所有顶点 \(x\) 的 transfer 向量做以下迭代：
More Effective PRT
SH Rotation
PRT 的一个问题是如果 lighting 部分是预计算的，那就只适用于静态环境光下的静态物体渲染；环境光或者物体只要有变化，PRT 就不得不进行重新预计算；但得益于 SH 的旋转不变性，我们至少可以让 SH Lighting 适用于动态旋转的情形而不必重新预计算。
注：环境光旋转和物体旋转在 PRT 渲染中是等价的（只是说看相对于哪个东西来看待旋转而已）。当然实践中，我们也可以对输入向量来进行反向旋转，来获得等同于环境光正向旋转的效果；只是如果考虑每次对输入向量进行旋转操作比较费的话，可以考虑一次性旋转完 SH lighting，就避免了输入向量旋转的操作了。
现在给定旋转 \(R\) ，然后有SH投影函数 \(P\)（输入一个球面向量，输出第 \(l\) 层band的 SH 系数向量组）。假设我们有 \(2l+1\) 个任意的球面向量，我们需要想办法求出能等价于旋转 \(n_i\) 的矩阵 \(M\) 来旋转 SH 投影函数 \(P\) ：
整理得：
记 \(A = [P_{(n−l)}, ..., P (n_{l})]\) ，如果矩阵 \(A\) 是可逆的，则：
这样，无论 \(R\) 怎么变化，我们都可以即时根据 \(R\) 求出 \(M\) ，然后把最新的 \(M\) 应用到所有预计算好的 \(P(\omega)\) 上（即预计算好的SH系数上），而不必重新预计算 \(P(R(\omega))\) 。
也就是要做 SH 的快速旋转实现，就需要对所有层进行处理，对于第 \(l\) 层 band 处理如下：
- 选取共 \(2l + 1\) 个 单位向量 \(n_i\)，这些向量 \(n_i\) 投影在该层 band 上的基函数就能得到系数 \(P (n_i)\)。共 \(2l + 1\) 个 \(2l+1\) 维向量 \(P (n_i)\) 构成了矩阵 \(A\)，并求出 \(A^{−1}\)
如何选取单位向量：要保证投影后构成的 \(A\) 矩阵可逆。
-
给定旋转 \(R\) ，对所有 \(n_i\) 依次做旋转 \(R(n_i)\) ，这些旋转后的单位向量同样投影在该层 band 上的基函数就能得到系数 \(P(R(n_i))\)。 共 \(2l + 1\) 个 \(2l + 1\) 维向量 \(P(R(n_i))\) 构成了矩阵 \(S\)
-
求出该层 band 上球谐函数的旋转矩阵 \(M = SA^{−1}\)
-
用 \(M\) 乘以该层 band 上的 SH 系数向量组就可以得到旋转后的 SH 系数向量组。
\(l=0\) 时只有1个系数，故不需要处理；\(l=1\) 时需要处理3个系数，其中的 \(A、S、M\) 将会是 3X3 矩阵；\(l=2\) 时需要处理5个系数，其中的 \(A、S、M\) 将会是 5X5矩阵......
最后，将每一层 band 的结果重新拼接起来即可得到完整的旋转后的 SH 系数结果。
// 伪代码：三阶SH旋转
SHCoeffientsAfterRotation(Array coeffients, Rotation rotation){
Array res;
// 处理 l = 0
res[0] = coffients[0];
// 处理 l = 1
// step 1
n1 = [1,0,0],n2 = [0,1,0],n3 = [0,0,1];
A = [ // SHProject(n,l,m)：向量n投影到SH中l层第m个基函数，输出对应系数
[SHProject(n1,1,-1),SHProject(n2,1,-1),SHProject(n3,1,-1)],
[SHProject(n1,1,0),SHProject(n2,1,0),SHProject(n3,1,0)],
[SHProject(n1,1,1),SHProject(n2,1,1),SHProject(n3,1,1)]
];
A_inv = InvMatrix(A);
// step 2
rn1 = rotation*n1,rn2 = rotation*n2,rn3 = rotation*n3;
S = [
[SHProject(rn1,1,-1),SHProject(rn2,1,-1),SHProject(rn3,1,-1)],
[SHProject(rn1,1,0),SHProject(rn2,1,0),SHProject(rn3,1,0)],
[SHProject(rn1,1,1),SHProject(rn2,1,1),SHProject(rn3,1,1)]
];
// step 3
M = S*A_inv;
// step 4
coeff_l1 = M*[coeffients[1],coeffients[2],coeffients[3]];
res[1] = coeff_l1[0];
res[2] = coeff_l1[1];
res[3] = coeff_l1[2];
// 处理 l = 2
// step 1
k = 1/sqrt(2);
n1 = [1,0,0],n2 = [0,0,1],n3 = [k,k,0],n4 = [k,0,k],n5 = [0,k,k];
A = [
[SHProject(n1,2,-2),SHProject(n2,2,-2),SHProject(n3,2,-2),SHProject(n4,2,-2),SHProject(n5,2,-2)],
[SHProject(n1,2,-1),SHProject(n2,2,-1),SHProject(n3,2,-1),SHProject(n4,2,-1),SHProject(n5,2,-1)],
[SHProject(n1,2,0),SHProject(n2,2,0),SHProject(n3,2,0),SHProject(n4,2,0),SHProject(n5,2,0)],
[SHProject(n1,2,1),SHProject(n2,2,1),SHProject(n3,2,1),SHProject(n4,2,1),SHProject(n5,2,1)],
[SHProject(n1,2,2),SHProject(n2,2,2),SHProject(n3,2,2),SHProject(n4,2,2),SHProject(n5,2,2)]
];
A_inv = InvMatrix(A);
// step 2
rn1 = rotation*n1,rn2 = rotation*n2,rn3 = rotation*n3,rn4 = rotation*n4,rn5 = rotation*n5;
S = [
[SHProject(rn1,2,-2),SHProject(rn2,2,-2),SHProject(rn3,2,-2),SHProject(rn4,2,-2),SHProject(rn5,2,-2)],
[SHProject(rn1,2,-1),SHProject(rn2,2,-1),SHProject(rn3,2,-1),SHProject(rn4,2,-1),SHProject(rn5,2,-1)],
[SHProject(rn1,2,0),SHProject(rn2,2,0),SHProject(rn3,2,0),SHProject(rn4,2,0),SHProject(rn5,2,0)],
[SHProject(rn1,2,1),SHProject(rn2,2,1),SHProject(rn3,2,1),SHProject(rn4,2,1),SHProject(rn5,2,1)],
[SHProject(rn1,2,2),SHProject(rn2,2,2),SHProject(rn3,2,2),SHProject(rn4,2,2),SHProject(rn5,2,2)]
];
// step 3
M = S*A_inv;
// step 4
coeff_l2 = M*[coeffients[4],coeffients[5],coeffients[6],coeffients[7],coeffients[8]];
res[4] = coeff_l2[0];
res[5] = coeff_l2[1];
res[6] = coeff_l2[2];
res[7] = coeff_l2[3];
res[8] = coeff_l2[4];
return res;
}
这样我们对 lighting 的 SH 系数做 rotation，就可以实现支持环境光旋转或物体旋转的实时 SH Lighting。
但是注意，不应当对 transfer 的 SH 系数做 rotation，因为一个物体的 transfer function 只考虑自身的几何遮蔽（自身与自身的遮蔽关系），而非像物体与环境光那样存在相对关系。
SH rotation 效果图：
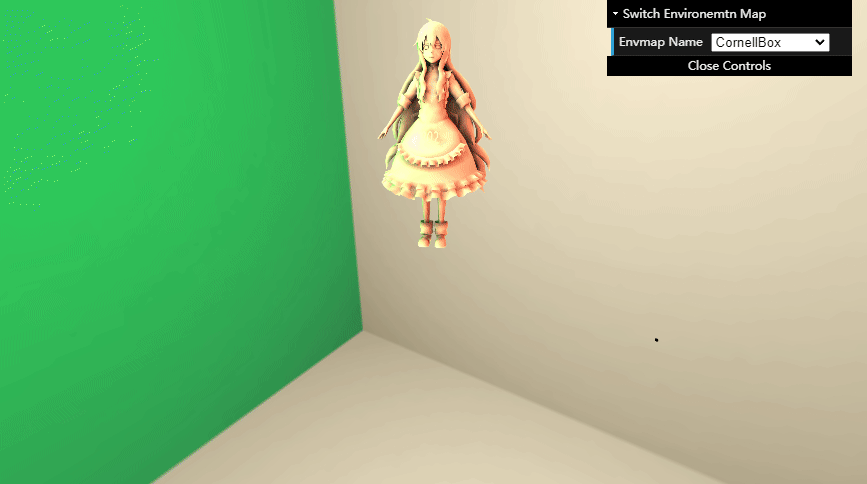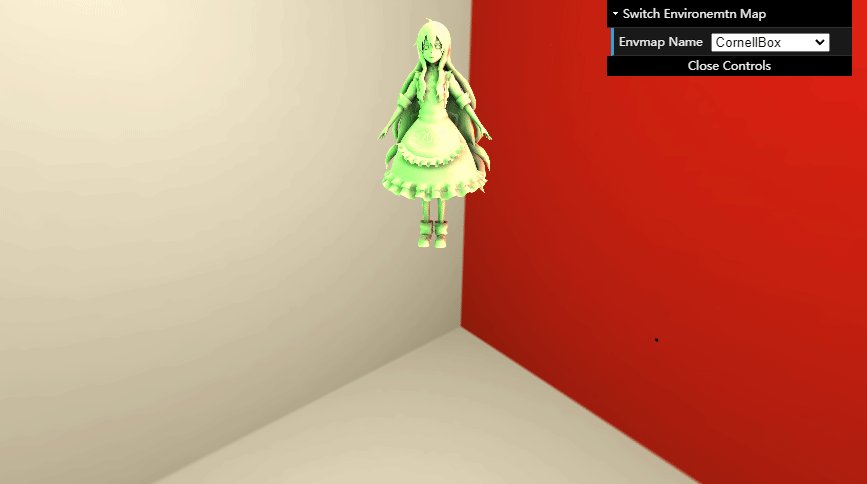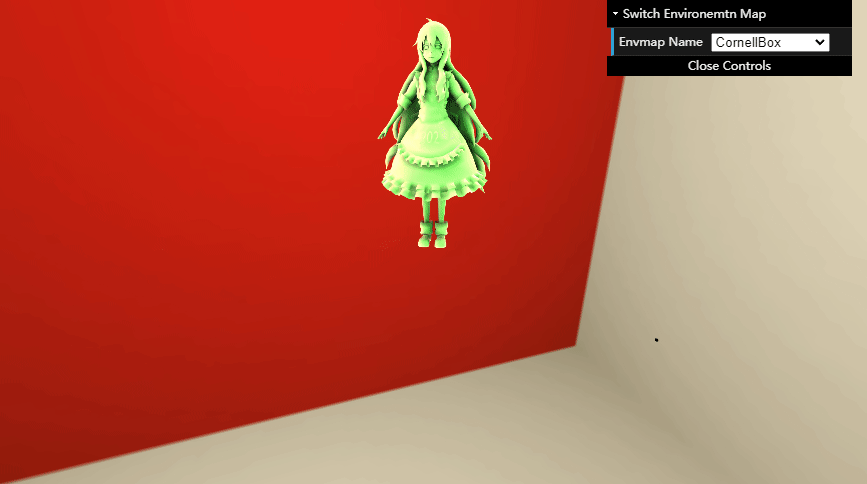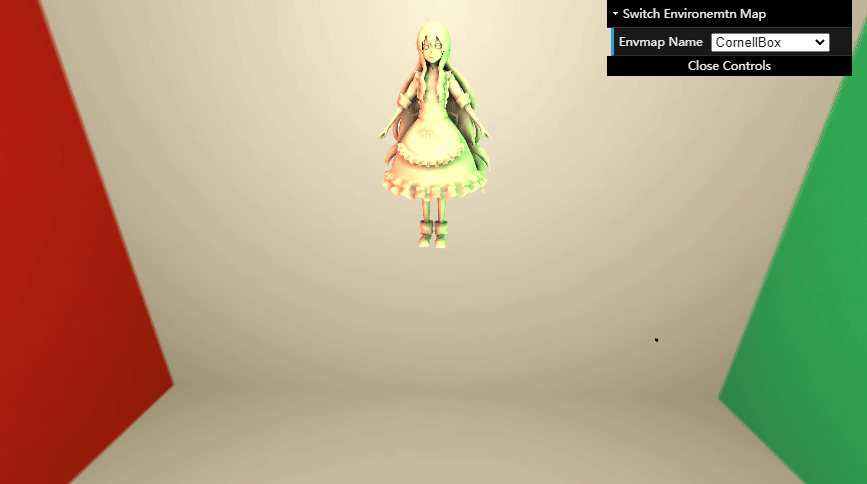
无需迭代的 Infinite-bounce Transfer
前面的 PRT 章节中，我们知道 diffuse 物体的 transfer 迭代公式如下：
要计算出 diffuse 物体的 infinite-bounce 的 transfer，理论上需要进行无限次迭代。然而我们可以利用一些假设来化简掉无限迭代，从而实现一次迭代算出 infinite-bounce 的 transfer 向量。
一个观察是点 \(x\) 与其发出射线能相交到的点 \(x'\) 的距离往往是比较近的（万一距离远了 \(x'\) 在积分计算中的贡献反正也比较少），因此它们的几何环境也是比较接近的。因此我们假设 \(x\) 和 \(x'\) 的 transfer 基本一致，即 \(x=x'\)。
因此原式可以移除无关参数，进一步化简为：
令 \(A = \rho \cdot \int_{\Omega^{+}}(1-V(\mathbf{\omega})) \cdot \max (0, n\cdot \mathbf{\omega}) \mathrm{d} \mathbf{\omega}\)
由于
- diffuse BRDF为 \(\rho = \frac{albedo}{\pi}\)，而一般 albedo 都会小于 1
- \(\int_{\Omega^{+}}(1-V(\mathbf{\omega})) \cdot \max (0, n\cdot \mathbf{\omega}) <= \pi\)
因此可得 \(A < 1\)
原递推式可得：
- \(T^{1} = T^0 + T^{0} \cdot A\)
- \(T^{2} = T^0 + T^{1} \cdot A\)
- ...
- \(T^{n} = T^0 + T^{n-1} \cdot A\)
递归代入后得：
等比数列求和得：
当 n 趋近于无穷时，又 \(A < 1\)，则最终收敛得到了结论
总结
无论 IBL 还是 PRT 都属于实现环境光照的方案，它们的区别在于：
- IBL 是一种从预计算环境光照出发的环境关照渲染方案：
- 采用环境贴图：存储占用空间较大，同时也占采样 I/O。
- 能保留高频信息，常用于 diffuse/glossy/specular 物体的渲染。
- PRT 是一种从预计算 transfer function 出发的环境光照渲染方案：
- 采用 SH lighting：存储开销和重建环境光照的开销极低。
- 只能保留低频信息，常用于 diffuse/glossy 物体的渲染。
- 效果上，相比 IBL 额外考虑了物体几何对环境光照的遮蔽效果。但只考虑了物体局部 transfer 效果，没有考虑完整场景 transfer 效果。不过在其它 PRT 方案中有支持完整场景的 transfer 效果。
- 物体不可局部形变，材质不可动态：若发生变化，那么其 transfer 就需要更新。
全局光照（Global Illumination,GI），严格意义上指完整的物理的间接光照效果，实际上只要有体现间接光效果（即使是部分效果或者 tricky 的效果）的光照都可称为 GI，因此它总体上分为两派：
- 有一派是通过一套统一标准的渲染流程把任何物体的 GI 计算出来，往往计算量极大但效果更加物理更加真实，典型的例子便是 path tracing
- 另一派是把 GI 的效果看成一个个部分来组成，这样我们可以选择其中一些 GI 效果组合使用，适应不同的性能（往往计算量相对低些，尤其是实时渲染）的同时也能带来能接受的 GI 效果（虽然往往不是严谨的物理正确），例如：在单个物体的角度上实现环境光照的局部自遮蔽/自反射效果（例如 PRT），在整个场景的角度来实现间接光照在全局场景 bounce 来 bounce 去的效果（例如 VXGI）。
参考
作者：KillerAery
出处：http://www.cnblogs.com/KillerAery/
本文版权归作者和博客园共有，未经作者同意不可擅自转载，否则保留追究法律责任的权利。
