游戏AI之路径规划

何为路径规划？

首先，我们简单了解下运动规划问题：在给定的位置A与位置B之间为机器人找到一条符合约束条件的路径。这种问题常出现在机器人、汽车导航等工业应用中。而路径规划则是运动规划里的重要研究内容。

所谓路径规划，就是指在一张已知的地图上，规划出一条位置A到位置B的路径。而运动规划里也有很多不知地图的情形，需要机器人自主去构建地图、自主摸索规划路径。

而对于游戏程序的运动规划问题，更多（甚至绝大部分）都是路径规划问题，因为游戏地图几乎总是已知的。因此本文主要列举一些可用于游戏程序的路径规划知识。

基本寻路算法

Dijkstra算法

经典的图算法，直接运用在游戏AI的寻路中效率会非常低，因此这里就不多说明了。

A* 寻路算法

A*寻路是游戏程序中最常用的寻路算法，没有之一，其大致思路就是Dijkstra算法结合贪心思想。
有关A*寻路算法的文章也满大街都有，这里就不多介绍，若不熟悉，可以参考博主的A*寻路算法。

A*寻路算法 - KillerAery - 博客园

B* 寻路算法

在写A*寻路算法总结笔记的时候，我还偶然发现了另一个号称效率更高的B*的算法，而且看了定义以后，发现概念也很简单。

B*算法类似于水往低处流的思路：

直接往目标点移动，若遇到障碍则尝试绕爬。
绕开后重复上述步骤。

该算法的确效率很高，但是它的路径结果往往不是最优的（当然非最优解的路径也适用于游戏AI，因为这能让玩家觉得AI路径自然。）

然而致命的是，当障碍物是凹多边形时（凹口朝向与玩家的探索方向相反时），B*算法很难实现绕爬出来，从而导致无解。

而网上资料展示的障碍往往没有提到这种障碍情况（绕爬需要至少两格宽度，而图示只有一格宽度，不可绕爬只可退步）：

一种解决方法是回溯绕爬，即限制最多可回退若干个节点，每次回退尝试一次绕爬，直到一次绕爬成功。
但是要是允许回溯过多节点，其复杂度会退化成DFS的程度，丧失了其效率高的特性。

总之，B*算法其实就是暴力的直觉寻路，它可能适合简单障碍的地图并且所需寻路不用较好的解或者不需要知道地图信息的无脑尝试绕爬的行为。综上，其实并不多可能运用于游戏开发中的路径规划中。

JPS/JPS+寻路算法（Jump Point Search/Plus）

JPS（jump point search）算法实际上是对A* 寻路算法的一个改进，因此在阅读本文之前需要先了解A*算法。

A* 算法在扩展节点时会把节点所有邻居都考虑进去，这样openlist中点的数量会很多，搜索效率较慢。

JPS 算法搜到的节点总是“跳跃性”的，都是从需要改变行走方向的拐点直接跳到另一个拐点，因此这也是 Jump Point 命名的来历。

JPS+ 算法则是在JPS算法基础上多了预处理的步骤，从而使寻路更加快速。

JPS/JPS+ 寻路算法 - KillerAery - 博客园

D* 寻路算法

TODO：待补充

对于一些静态的游戏场景来说，A*算法是很好的选择。但是如果障碍是动态的，例如移动的车辆堵住了路...A*算法可能得时时重新计算路径才能保证适应动态场景，这开销无疑是巨大的。而D*寻路算法正是用于解决动态障碍场景问题的一种寻路算法。

寻路节点

使用路径点（Way Point）作为节点

大部分讨论A*算法使用的节点是网格点（也就是简单的二维网格），但是这种内存开销往往比较大。
实际上A*寻路算法，对于图也是适用的，实现只要稍微改一下。

因此我们可以把地图看作一个图而不是一个网格，使用预先设好的路径点而不是网格来作为寻路节点，则可以减少大量节点数量。

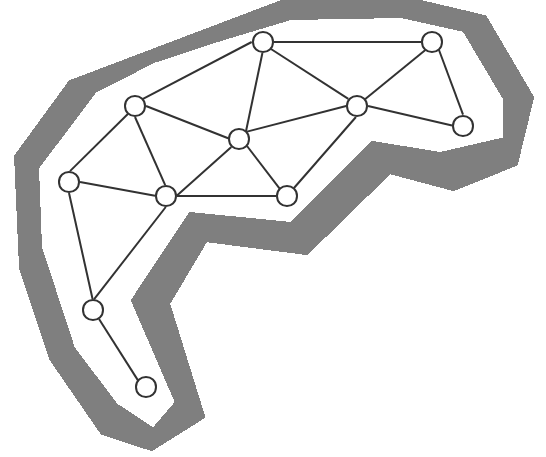
（如图，使用了路径点作为节点，路径点之间的连线表示两点之间可直接移动穿过）

使用路径点的好处：

减少大量节点数量，顺带也就减少了寻路的运算速度开销。
相比网格节点，路径点的路径更加平滑。

多层次路径点

在育碧的游戏《Assassin's Creed: Origins》里，地图大的令人发指（也许有整个埃及地区的大小）。而大地图的寻路是一种比较头疼的问题。为了实现长距离导航(Long range navigation)，地图采用了路径点作为节点，同时采用了三层次节点的划分。

寻路首先是发生在最高层次上（图为黄色部分节点），需要先找到离玩家最近的和离终点最近的黄色层次节点。

然后根据找到的2个节点，在它们的所属区块里再寻找离玩家/终点最近的绿色层次节点，从而找到绿色节点到达黄色节点的方法。

同理，在2个绿色层次节点所属区块（更小的区块）寻找离玩家/终点最近的白色层次节点。

最后找到的三个层次节点相连接，便是一条长距离导航路径。

导航网格将地图划分成若干个凸多边形，每个凸多边形就是一个节点。
使用导航网格更加可以大大减少节点数量，从而减少搜寻所需的计算量，同时也使路径更加自然。

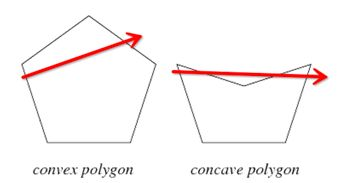
使用凸多边形，是因为凸多边形有一个很好的特性：边上的一个点走到另外一点，不管怎么走都不会走出这个多边形。而凹多边形可能走的出外面。

然而该如何建立地图的导航网格，一般有两种方法：

手工划分导航网格往往工作量巨大。
程序化生成导航网格则实现稍微复杂。

导航网格是目前3D游戏的主流实现，例如《魔兽世界》就是典型使用导航网的游戏，Unity引擎也内置了基于导航网格的寻路系统。

如果你对如何将一个区域划分成多个凸多边形作为导航网格感兴趣，可以参考空间划分的数据结构(网格/四叉树/八叉树/BSP树/k-d树/BVH/自定义划分) - KillerAery - 博客园里面的BSP树部分，也许会给你一些启发。

预计算

主要方式是通过预先计算好的数据，然后运行时使用这些数据减少运算量。
可以根据自己的项目权衡运行速度和内存空间来选择预计算。

洪水填充法（Floodfill）自动创建路径点

倘若一个地图过大，开发人员手动预设好路径点+路径连接的工作就比较繁琐，而且很容易有错漏。
这时可以使用洪水填充算法来自动生成路径点，并为它们链接。

算法步骤：
1.以任意一点为起始点，往周围八个方向扩展点（不能通行的位置则不扩展）

2.已经扩展的点（在图中被标记成红色）不需要再次扩展，而扩展出来新的点继续扩展

3.直到所有的点都被扩展过，此时能得到一张导航图

//洪水填充法:从一个点开始自动生成导航图
void generateWayPoints(int beginx, int beginy, std::vector<WayPoint>& points) {
	//需要探索的点的列表
	std::queue<WayPoint*> pointsToExplore;
	//生成起点，若受阻，不能生成路径点，则退出
	if (!canGeneratePointIn(beginx, beginy))return;
	points.emplace_back(WayPoint(beginx, beginy));
	//扩展距离
	float distance = 2.3f;
	//预先写好8个方向的增量
	int direction[8][2] = { {1,0}, {0,1}, {0,-1}, {-1,0}, {1,1}, {-1,1}, {-1,-1},{1,-1} };
	//以起点开始探索
	WayPoint* begin = &points.back();
	pointsToExplore.emplace(begin);
	//重复探索直到探索点列表为空
	while (!pointsToExplore.empty()) {
		//先取出一个点开始进行探索
		WayPoint* point = pointsToExplore.front();
		pointsToExplore.pop();
		//往8个方向探索
		for (int i = 0; i < 8; ++i) {
			//若当前点的目标方向连着点，则无需往这方向扩展
			if (point->pointInDirection[i] == nullptr) {
				continue;
			}
			auto x = point->x + direction[i][0] * distance;
			auto y = point->y + direction[i][1] * distance;
			//如果目标位置受阻，则无需往这方向扩展
			if (!canGeneratePointIn(x, y)) {
				continue;
			}
			points.emplace_back(WayPoint(x, y));
			auto newPoint = &points.back();
			pointsToExplore.emplace(newPoint);
			//如果当前点能够无障碍通向目标点，则连接当前点和目标点
			if (canWalkTo(point, newPoint)) {
				point.connectToPoint(newPoint);
			}
		}
	}
}

自动生成的导航图可以调整扩展的距离，从而得到合适的节点和边的数量。同时也可以调整扩展方向，再加入一定随即噪音作为距离和方向的参数，可以实现随机扩展的效果，从而得到更加自然的路径。

路径查询表/路径成本查询表

借助预先计算好的路径查询表，可以以O(|v|)的时间复杂度极快完成寻路，但是占用空间为O(|v|²)。
（|v|为顶点数量）

实现：对每个顶点使用Dijkstra算法，求出该顶点到各顶点的路径，再通过对路径回溯得到前一个经过的点。

有时候，游戏AI需要考虑路径的成本来决定行为，
则可以预先计算好路径成本查询表，以O（1）的时间复杂度获取路径成本，但是占用空间为O(|v|²)。

实现：类似路径查询表，只不过记录的是路径成本开销，而不是路径点。

扩展障碍碰撞几何体

在寻路中，一个令游戏AI程序员头疼的问题是碰撞模型往往是一个几何形状而不是一个点。
这意味着在寻路时检测是否碰到障碍，得用几何形状与几何形状相交判断，而非几何形状包含点判断（毋庸置疑前者开销庞大）。

一个解决方案是根据碰撞模型的形状扩展障碍几何体，此时碰撞模型可以简化成一个点，这样可以将问题由几何形状与几何形状相交问题转换成几何形状包含点问题。

这里主要由两种扩展思路：

碰撞模型的各个顶点与障碍几何体顶点重合，然后扫过去锚点形成的边界即是扩展的边界（实际上就是让碰撞模型紧挨着障碍几何体走一圈）

碰撞模型的锚点与障碍几何体顶点重合，然后扫过去最外围顶点形成的边界即是扩展的边界（实际上就是让碰撞模型沿着原几何体边界走一圈）

这些扩展障碍几何形状的计算完全可以放到预计算（离线计算），不过要注意：

各个需要寻路的碰撞模型最好统一形状，这样我们只需要记录一张（或少量）扩展过的障碍图。
碰撞模型不可以是圆形，因为这样扩展出的障碍几何体将是圆曲的，很难计算。一个解决方案是用正方形近似替代圆形来生成扩展障碍几何体。
当遇到非凸多边形障碍时，在凹处可能会出现扩展出的顶点重复（交点），简单的处理是凹角处不插入新的点。

Goal Bounding

Goal Bounding是一种节点裁剪技术，可加快寻路速度。Goal Bounding为每个节点的边（Edge）计算一个节点集合，该集合至少包含通过该边可到达最短路的所有节点。

为了让节点集合支持快速查询是否含有目标节点的功能，往往需要使用特定形状表示集合（例如用4个int值来表示轴对齐的AABB盒），这也使得该集合包含了一定数量的无关节点。因此，用于Goal Bounding技术的节点集合也被称为Goal Bounds。

下图图示，左侧为绿色节点通过左边可达最短路径的所有节点，右侧为绿色节点计算出来的通过左边的Goal Bounds：

下图图示，为使用NavMesh节点时计算出的Goal Bounds，NavMesh 天生具有不规则的形状，幸好AABB盒仍然能很好的表示集合，只是会有更多多余的无关节点。

在通过某个边缘（即朝某个方向）搜索时，只有目标节点包含在通过该边的节点集合时，才会搜索该方向，否则该方向没必要搜索。
Goal Bounding 可以使用在任何寻路算法（Dijkstra、A*、JPS+等）应用于任何搜索空间（网格，图形，NavMesh等）。
Goal Bounding 的缺点在于必须使用\(O(n^2)\)时间对 Goal Bounding 数据进行预处理，因此无法支持对搜索空间进行动态运行时修改（添加或删除边/墙）。其次，Goal Bounding 要求\(O(n)\)的存储空间（Goal Bounds形状为AABB盒且地图为网格时，每个节点有8个边，每个边需要存储4个值，即总共 \(32n\) 个值）。

对某个节点计算Goal Bounds的大致过程如下（以A*算法、网格地图、8方向为例）：

从该节点出发，先朝八个方向各移动一格，将8个方向移动后的位置记录在对应的8个队列里。（这一步是为了保证搜索通过了目标方向。）
8个队列进行一轮移动：每个队列取出队首节点后，从该节点向8个方向移动一格。每移动到新的位置则记录在集合里，重复走过的位置（若是本轮中其它队列走过的位置，则依然视为本队列的新位置）则不需再记录。此外，每个队列每个取出过的节点需放入对应的集合（8个集合）。
重复步骤2，直到八个队列都为空，这意味着无论哪个方向都走到了尽头（边界或障碍）。
对其中一个集合进行遍历，提取出其中最大、最小的y值和最大、最小的x值，这个便作为Goal Bounds的AABB形状的表示。此时便代表本节点的一个方向的Goal Bounds计算完毕。
重复步骤4，直到本节点八个方向的Goal Bounds都计算完毕。

在 GDC 2015 JPS+ with Goal Bounding的演讲上，Steve Rabin 给出了结合 JPS+ 和 Goal Bounding 的方案，效果非常好。

可视点寻径

TODO 待更新

启发函数

我们知道在A*算法里，启发函数\(f(n) = g(n)+h(n)\) 是非常重要的组成部分。

其中 \(g(n)\) 为从起点走到该节点的总共耗费值，预测值为 \(h(n)\) 从该节点走到终点的预测耗费值。

A*算法是最优解吗？

很多人认为A*算法构建的路径并不是最优解，但实际上是否最优解取决于启发函数的一致性。

启发函数的一致性：1. 节点启发函数值需单调不递减 2. 节点启发函数的值小于等于经过该节点的整条路径的实际开销值。

也就是说，只要保证启发函数的一致性，那么A*算法就一定能找到最优解。

这里做一个简单的解释：地图存在一条路径 \(p1\) 为实际最短路径，实际总开销为 \(c_1\)。假设A*寻路算法即将寻得另一条路径 \(p2\) 作为最短路（也就是说openlist添加了 \(p2\) 路径上最后一个节点（终点） \(n_{end}\)），实际总开销为 \(c_2\)（\(c_1 < c_2\)）。
该节点的启发函数 \(f_2(n_{end}) = g_2(n_{end})+h_2(n_{end})\)，由于此时 \(g_2(n_{end})\) 已经变为整条路径的实际开销 \(c_2\)，加上一致性保证，于是有
\(f_2(n_{end}) = c_2\)
又由于一致性保证，\(p1\) 任一节点启发函数 \(f_1(n)\) 估值总是小于等于 \(p1\) 的实际开销，而 \(p1\) 的实际开销又小于 \(p2\) 的实际开销，因此有
\(f_1(n) <= c_1 < c_2 = f_2(n_{end})\)
此时A*寻路算法开启的下一个节点若为放入openlist里 \(p2\) 的终点\(n_{end}\)，那么必须先将 \(p1\) 路径上所有节点开启完毕，此时 \(p1\) 最后一个节点（终点）启发函数值 \(f_1(n_{end}) < f_2(n_{end})\)，即A*算法最终必然还是寻得 \(p1\) 作为最短路。

启发函数由耗费值 \(g(h)\) 和预测值 \(h(n)\) 相加而成，其中耗费值基本是不需关注的，因为耗费值总意味着实际的已耗费值，是准确的。而预测函数是我们需要重点关注的改进点。一个好的预测函数不仅能保证较好（或最好）的解，还可以带来很高的启发效率。

\(h(n) = 0\)，意味着 \(f(n) = g(n)\)，此时A星算法则退化成了Dijkstra算法，效率十分低。
\(h(n) < cost(n)\)，搜索效率略低，h(n)越小，意味着搜索节点越多，效率上越低。
\(h(n) = cost(n)\)，是A*算法最高效的情形。
\(h(n) > cost(n)\)，不可以保证一致性，\(h(n)\) 越小，寻得的路越接近最优解。

对于网格形式的地图，如果单纯的用距离来代表耗费，则有以下这些预测函数 \(h(n)\) 可以保证启发函数一致性：

如果只允许朝上下左右四个方向移动，则使用曼哈顿距离（Manhattan distance）。
如果允许朝任何方向（或八个方向）移动，则使用欧几里得距离（Euclidean distance）。

战术评估

在游戏中的寻路里，我们不一定追求最优解的路径；其次对于复杂的游戏世界来说，特别是对于需要复杂决策的AI来说，节点的预测值也不仅仅就距离一个影响因素：

地形优势：例如平地节点走得更快而山地节点走得更慢。
视野优势：某些地方具有良好的视野（例如高地），AI需要准备战斗时应该倾向占领视野优势点。
战术优势：一些地方（例如刷出医疗包的地点，可操控机枪）提供了战术优势，AI应倾向占领这些战术优势地点。
其他...

因此，我们可以自定义启发函数，以调整成为适应复杂游戏世界的AI寻路。

加权优化

A*算法按照传统的启发函数进行路径搜索时，会不断往返搜索，搜索节点过多。如果我们减轻离终点比较接近的节点启发函数值，那么A*算法会更有可能优先开启这些节点，这就是加权优化的核心思想。

同时，于是最直观的想法是加大启发函数中 \(h(n)\) 的权重，公式如下：

\(f(n)=g(n)+k*h(n)\)

式中 \(k\) 为权重。离终点较远节点的预测值往往很大，乘了权重后整个启发函数值会变得更大，从而更多可能开启离终点较近节点。

在上述式子的基础上，在进行指数衰减的方式的加权，如下式子：

\(f(n)=g(n)+ exp⁡[h(n)]*h(n)\)

这样我们可以有如下效果：

当h(n)较大时，权重大，这样使节点迅速向终点行进。
当h(n)较小时，权重小。
终点附近时，权重接近1，可保证终点可达。

无论是直接单个k系数，还是使用指数衰减，无非都是关于 \(h(n)\) 权重的配比问题。总之，在设计加权时，可以考虑如下：

当节点离终点较远时，权重应该大一些；当节点逐渐靠近终点时，权重随之变小。
尽可能让启发函数值不要太大（小于等于实际路径代价是最好的，可有一致性）。
当节点到达终点时，启发函数值 \(f(n)\) 等于实际值。

其它改进

平均帧运算

有时候，大量物体使用A*寻路时，CPU消耗比较大。
我们可以不必一帧运算一次寻路，而是在N帧内运算一次寻路。
（虽然有所缓慢，但是就几帧的东西，一般实际玩家的体验不会有大影响）

所以我们可以通过每帧只搜索一定深度 = 深度限制 / N（N取决于自己定义多少帧内完成一次寻路）。

路径平滑

基于网格的寻路算法结果得到的路径往往是不平滑的。

（下图为一次基于网格的正常寻路算法结果得到的路径）

（下图为理想中的平滑路径）

很容易看出来，寻路算法的路径太过死板，只能上下左右+斜45度方向走。

这里提供两种平滑方式：

快速而粗糙的平滑

它检查相邻的边是否可以无障碍通过，若可以则删除中间的点，不可以则继续往下迭代。

它的复杂度是O（n）,得到的路径是粗略的平滑，还是稍微有些死板。

void fastSmooth(std::list<OpenPoint*>& path) {
    //先获取p1,p2,p3，分别代表顺序的第一/二/三个迭代元素。
    auto p1 = path.begin();
    auto p2 = p1; ++p2;
    auto p3 = p2; ++p2;
    while (p3 != path.end()) {
        //若p1能直接走到p3，则移除p2，并将p2,p3往后一位
        // aa-bb-cc-dd-...  =>  aa-cc-dd-...
        // p1 p2 p3             p1 p2 p3
        if (CanWalkBetween(p1, p3)) {
            ++p3;
            p2 = path.erase(p2);
        }
        //若不能走到，则将p1,p2,p3都往后一位。
        // aa-bb-cc-dd-...  =>  aa-bb-cc-dd-...
        // p1 p2 p3                p1 p2 p3
        else {
            ++p1;
            ++p2;
            ++p3;
        }
    }
}

精准而慢的平滑

它每次推进一位都要遍历剩下所有的点，看是否能无障碍通过，推进完所有点后则得到精准平滑路径。

它的复杂度是O（n²）,得到的路径是精确的平滑。

void preciseSmooth(std::list<OpenPoint*>& path) {
    auto p1 = path.begin();
    while (p1 != path.end()) {
        auto p3 = p1; ++p3; ++p3;
        while (p3 != path.end()) {
            //若p1能直接走到p3，则移除p1和p3之间的所有点,并将p3往后一位
            if (CanWalkBetween(p1, p3)) {
                auto deleteItr = p1; ++deleteItr;
                p3 = path.erase(deleteItr,p3);
            }
            //否则，p3往后一位
            else {
                ++p3;
            }
        }
        //推进一位
        ++p1;
    }
}

双向搜索（Bidirectional Search）

与从开始点向目标点搜索不同的是，你也可以并行地进行两个搜索：
一个从开始点向目标点，另一个从目标点向开始点。当它们相遇时，你将得到一条路径。

双向搜索的思想是：单向搜索过程生成了一棵在地图上散开的大树，而双向搜索则生成了两颗散开的小树。
一棵大树比两棵小树所需搜索的节点更多，所以使用双向搜索性能更好。

以BFS寻路为例，黄色部分是单向搜索所需搜索的范围，绿色部分则是双向搜索的，很容看出双向搜索的开启节点数量相对较少：

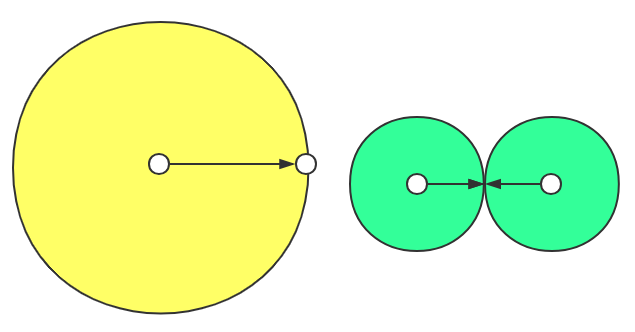
应用于A*算法的双向搜索放入openlist的节点为红色和蓝色部分，而传统的单向搜索则不仅包含红色、蓝色，还包括了灰色部分：

不过在部分场景，双向搜索的性能反而会比单向搜索更加差（图示中，A*算法使用单向搜索时，起点几乎搜索了整个自己的房间，在进入另一个房间时才几乎可以直线到达终点，而双向搜索让两个起点都不得不搜索了各自整个房间）：

为了避免这些情况的出现，Nathan Sturtevant在GDC 2018提到了一个名为 NBS 的数据结构用以辅助，使得双向搜索最差情况下比最好的单向搜索情况慢一点点。

路径拼接

游戏世界往往很多动态的障碍，当这些障碍挡在计算好的路径上时，我们常常需要重新计算整个路径。但是这种简单粗暴的重新计算有些耗时，一个解决方法是用路径拼接替代重新计算路径。

首先我们需要设置 拼接路径的频率K：
例如每K步检测K步范围内是否有障碍，若有障碍则该K步为阻塞路段。

接着，与重新计算整个路径不同，我们可以重新计算从阻塞路段首位置到阻塞路段尾的路径：
假设p[N]..P[N+K]为当前阻塞的路段。为p[N]到P[N+K]重新计算一条新的路径，并把这条新路径拼接（Splice）到旧路径：把p[N]..p[N+K]用新的路径值代替。

一个潜在的问题是新的路径也许不太理想，下图显示了这种情况(褐色为障碍物)：

最初正常计算出的路径为红色路径（1 -> 2 -> 3 -> 4）。
如果我们到达2并且发现从2到达3的路径被封锁了，路径拼接技术会把（2 -> 3）用（2 -> 5 -> 3）取代，结果是寻路体沿着路径（1 -> 2 -> 5 -> 3 -> 4）运动。
我们可以看到这条路径不是这么好，因为蓝色路径（1 -> 2 -> 5 -> 4）是另一条更理想的路径。

一个简单的解决方法是，设置一个阈值 最大拼接路径长度M：
如果实际拼接的路径长度大于M，算法则使用重新计算路径来代替路径拼接技术。

M不影响CPU时间，而影响了响应时间和路径质量的折衷：

如果M太大，物体的移动将不能快速对地图的改变作出反应。
如果M太小，拼接的路径可能太短以致于不能正确地绕过障碍物，出现不理想的路径，如（1 -> 2 -> 5 -> 3 -> 4）。

路径拼接确实比重计算路径要快，但它可能算出不怎么理想的路径：

若经常发现这种情况出现，那么重新计算整条路径也不失为一个解决办法。
尝试使用不同的M值和不同的拼接频率K(如每 \(\frac{3}{4}M\) 步)以用于不同的情形。
此外应该使用栈来反向保存路径，因为删除和拼接都是在路径尾部进行的。

参考

国外一篇博客总结了较多较全面的路径规划主题 Amit’s A* Pages
国外博客翻译版浅谈路径规划算法 - 简书
Bryan Stout 有两个算法，Patch-One和Patch-All，他从路径拼接中得到灵感，并在实践中运行得很好：Embodied-Agents-in-Dynamic | GDC 2007
Virtual Insanity: Meta AI on 'Assassin's Creed: Origins' | GDC 2018
《游戏编程精粹2(Game Programming Gems 2)》 Mark DeLoura [2001-10]
《游戏编程精粹3(Game Programming Gems 3)》 Dante Treglia [2002-7]
《游戏编程精粹5(Game Programming Gems 5)》 Kim.Pallister [2007-9]
国外一个AI运动规划的权威论坛 Moving AI Lab
JPS+: Over 100x Faster than A* | GDC 2015
Bidirectional-Search-Is-It-for | GDC 2018

游戏AI 系列文章：https://www.cnblogs.com/KillerAery/category/1229106.html

posted @ 2019-02-01 21:12 KillerAery 阅读(14227) 评论(7) 编辑收藏举报

刷新页面返回顶部

KillerAery