【复健】最小生成树-Kruskal
最小生成树(Kruskal)复健
Update
\(07.30.23 \ 08:28\) 增加了例题:P2820
\(07.30.23 \ 09:14\) 增加了例题:P2330
\(07.30.23 \ 10:35\) 增加了例题:联络员
\(07.30.23 \ 14:31\) 想起来生成树有个前提是联通图。
\(07.31.23 \ 06:58\) 增加了例题:最小差值生成树
\(07.31.23 \ 08:05\) 增加了例题:P2916
Before
考虑到要复健,就挑了OJ上一道比较简单的板子题,然后发现OI这东西一年不碰是真的可怕。
全文基本上是对21年学习笔记的扩充和新的理解,代码上的注释是我敲题的时候怕自己看不懂自己在写什么留的一些理解。
学术性低于自言自语含量
最小生成树
在一张无向联通图中,找出一棵边权和最小的树。
树
树是一种数据结构,它是由 \(n(n ≥ 0)\) 个有限节点组成一个具有层次关系的集合。
其实这句话没有什么用,节点肯定是有限的,层次关系也不清楚到底是什么样的层次关系
可以理解成由一个根节点不断分出其它的儿子节点,再由儿子节点继续分出另外的儿子节点的单向结构。
树的边是无向边,这里说的单向结构是指,从一个节点出发无法再回到这个节点。
由于树结构的特殊性,同一层的儿子节点之间必然无法直接连通(即被一条边连接)。
kruskal算法
\(Kruskal\) 是基于贪心实现的一种离线算法(话说最小生成树可以在线求吗,没了解过 \(Prim\)
它的主要思想是,排序后,每次取边权最小的边,如果这条边会形成环就删除,否则就把这条边加入答案。这里判断是否形成环运用了简单的并查集思想。
我将两个点看作一条边的“端点”,把连接端点的所有边都看做一条边,即“最长边”。如果最长边的两个端点是同一个点,那么说明这条“最长边”代表的所有边连成了一个环。
刚才也说过树是无法从一个节点出发再回到这个节点的,所以算法应该排除环。
我们利用一个 \(cnt\) 变量来记录目前选择的边数。我们知道一棵树的边数是这棵树所有节点(包括根节点与叶子节点)数 \(-1\),所以当达到了这个数目就退出即可。
注意
最开始时每个点都没有边连接,所以它们的另一个端点都是自己。
用链式前向星存图,存的边是有向的,需要反向再存一遍。
题目
最优布线问题
展开题面
学校有 \(n\) 台计算机,为了方便数据传输,现要将它们用数据线连接起来。两台计算机被连接是指它们间有数据线连接。由于计算机所处的位置不同,因此不同的两台计算机的连接费用往往是不同的。
当然,如果将任意两台计算机都用数据线连接,费用将是相当庞大的。为了节省费用,我们采用数据的间接传输手段,即一台计算机可以间接的通过若干台计算机(作为中转)来实现与另一台计算机的连接。
现在由你负责连接这些计算机,任务是使任意两台计算机都连通(不管是直接的或间接的)。
是一道很简单的板子题,需要注意的是输入格式:
第一行为整数 \(n(2 \le n \le 100)\),表示计算机的数目。
此后的 \(n\) 行,每行 \(n\) 个整数。第 \(x+1\) 行 \(y\) 列的整数表示直接连接第 \(x\) 台计算机和第 \(y\) 台计算机的费用。
展开代码
#include <bits/stdc++.h>
#define ll long long
#define MyWife Cristallo
using namespace std;
const int N = 1e4 + 5; //n = 100,那最多有 n * n = 1e4 条边(图是无向图,但是输入数据的边是有向边)
//其实这里应该也去除一下自环,不过在空间正常范围内开大点没什么坏处
int n, F[N], ans, cnt; //因为懒所以F数组干脆也用 1e4 + 5 了
struct edge {
int u, v, w;
} e[N]; //好像纯数组做不了这个题(大悲
bool cmp(edge a, edge b) {
return a.w < b.w; //贪心
} //忘了重载运算符怎么写了
int find(int x) {
if(F[x] == x) return x;
return F[x] = find(F[x]); //*一开始打成 find(x) 了,警钟长鸣*
}
int weal, tot;
void kruskal() {
sort(e + 1, e + 1 + tot, cmp); //数组下标从1开始
for(int i = 1; i <= tot; ++i) { //tot是下面主函数记录边数的变量,实际上就是 n * n。
int fa_u = find(e[i].u), fa_v = find(e[i].v); //我现在的理解是,对于边 e_i,其出度和入度各有所属的“端点”,这两个端点就是e_i实际上所参与连接的那条“最长边”的端点
if(fa_u == fa_v) continue; //可以看出,如果“最长边”的端点是同一个节点,那么就出现了环。根据树的定义可以排除这种情况。
ans += e[i].w, F[fa_u] = fa_v; //处理答案。现在 fa_u 和 fa_v 两个端点连接起来了,那么要让 fa_u 的“端点”变成 fa_v。
if(++cnt == n - 1) return;
}
}
int main() {
scanf("%d", &n);
for(int i = 1; i <= n; i++) F[i] = i; //*忘记初始化调好久,警钟长鸣*
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= n; ++j) {
scanf("%d", &weal);
e[++tot].u = i, e[tot].v = j, e[tot].w = weal;
}
} //存边的时候是有向边!!!
kruskal();
printf("%d\n", ans);
return 0;
}
局域网
题面:P2820
调了半个早上,不知道为什么MLE,最后发现:
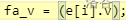
值得注意的只有需要输出的是剩下的边的边权和。
展开代码
#include <bits/stdc++.h>
#define ll long long
#define MyWife Cristallo
using namespace std;
const int N = 2 * 1e4 + 5, M = 105;
struct edge {
int u, v, w;
} e[N];
int n, k, ans, sum, cnt, F[M];
bool cmp(edge a, edge b) {
return a.w < b.w;
}
int find(int x) {
if(F[x] == x) return x;
return F[x] = find(F[x]);
}
void kruskal() {
sort(e + 1, e + 1 + k, cmp);
for(int i = 1; i <= k; ++i) {
int fa_u = find(e[i].u), fa_v = find(e[i].v);
if(fa_u == fa_v) continue;
ans += e[i].w, F[fa_u] = fa_v;
if(++cnt == n - 1) return;
}
}
int main() {
scanf("%d%d", &n, &k);
for(int i = 1; i <= n; ++i) F[i] = i;
for(int i = 1; i <= k; ++i) {
scanf("%d%d%d", &e[i].u, &e[i].v, &e[i].w);
sum += e[i].w;
}
kruskal();
printf("%d\n", sum - ans);
return 0;
}
[SCOI2005]繁忙的都市
题面:P2330
题意对于我这种阅读苦手来说不太友好\kk
总之是选一些能连成最小生成树的道路来改造,注意输出是选出道路的数量和生成树中边权最大的那条边。
展开代码
#include <bits/stdc++.h>
#define ll long long
#define MyWife Cristallo
using namespace std;
const int N = 1e5 + 5;
struct edge {
int u, v, w;
} e[N];
int n, m, sum, ans, cnt, F[N];
bool cmp(edge a, edge b) {
return a.w < b.w;
}
int find(int x) {
if(F[x] == x) return x;
return F[x] = find(F[x]);
}
void kruskal() {
sort(e + 1, e + 1 + m, cmp);
for(int i = 1; i <= m; ++i) {
int fa_u = find(e[i].u), fa_v = find(e[i].v);
if(fa_u == fa_v) continue;
++sum, ans = max(ans, e[i].w), F[fa_u] = fa_v;
if(++cnt == n - 1) return;
}
}
int main() {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++i) F[i] = i;
for(int i = 1; i <= m; ++i) scanf("%d%d%d", &e[i].u, &e[i].v, &e[i].w);
kruskal();
printf("%d %d\n", sum, ans);
return 0;
}
联络员
展开题面
Tyvj已经一岁了,网站也由最初的几个用户增加到了上万个用户,随着Tyvj网站的逐步壮大,管理员的数目也越来越多,现在你身为Tyvj管理层的联络员,希望你找到一些通信渠道,使得管理员两两都可以联络(直接或者是间接都可以)。Tyvj是一个公益性的网站,没有过多的利润,所以你要尽可能的使费用少才可以。
目前你已经知道,Tyvj的通信渠道分为两大类,一类是必选通信渠道,无论价格多少,你都需要把所有的都选择上;还有一类是选择性的通信渠道,你可以从中挑选一些作为最终管理员联络的通信渠道。数据保证给出的通行渠道可以让所有的管理员联通。
关于必选的处理:
因为是必选的,所以可以不让这条边进入待选位,即不将其加入 \(e\) 数组,不用kruskal去处理它。直接标记它所在最长边的两个端点,并在答案中加入它的权值即可。
展开代码
#include <bits/stdc++.h>
#define ll long long
#define MyWife Cristallo
using namespace std;
const int N = 1e5 + 5;
struct edge {
int u, v, w;
} e[N];
int n, m, ans, cnt, F[N];
bool cmp(edge a, edge b) {
return a.w < b.w;
}
int find(int x) {
if(F[x] == x) return x;
return F[x] = find(F[x]);
}
void kruskal() {
sort(e + 1, e + 1 + m, cmp);
for(int i = 1; i <= m; ++i) {
int fa_u = find(e[i].u), fa_v = find(e[i].v);
if(fa_u == fa_v) continue;
ans += e[i].w, F[fa_u] = fa_v;
if(++cnt == n - 1) return;
}
}
int main() {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++i) F[i] = i;
for(int i = 1; i <= m; ++i) {
int p, u, v, w;
scanf("%d%d%d%d", &p, &u, &v, &w);
if(p == 1) F[find(u)] = F[find(v)], ans += w;
else e[i] = {u, v, w};
}
kruskal();
printf("%d\n", ans);
return 0;
}
最小差值生成树
展开题面
CodeWaySky 很早就学了最小生成树,所以CodeWaySky 现在对简单的求最小生成树不感兴趣了。现在 CodeWaySky 想知道,对于一个给定的图,它的所有生成树中,最大边和最小边的边权差最小是多少。
因为 CodeWaySky 这个技术人员实在太忙了,到处帮大家解决问题,无法脱身,所以这个问题就交给你来解决了。
读了好久的题,最后发现是求一个生成树,使得这棵生成树内边权最大的边与边权最小的边的差值最小。
可以考虑 \(Kruskal\) 每跑一条边,就跑一个这条边是最小边的最小生成树。因为这里的生成树是以这条边为最小边的,所以生成树不是最小的,最大边就必然大,从而导致差值变大。
注意:
若图本身不连通,则输出 \(-1\)
展开代码
#include <bits/stdc++.h>
#define ll long long
#define MyWife Cristallo
using namespace std;
const int N = 1e4 + 5, M = 105;
struct edge {
int u, v, w;
} e[N];
int n, m, ans = 0x7fffffff, cnt, F[M], tot;
bool cmp(edge a, edge b) {
return a.w < b.w;
}
int find(int x) {
if(F[x] == x) return x;
return F[x] = find(F[x]);
}
void kruskal() {
sort(e + 1, e + 1 + m, cmp);
for(int i = 1; i <= m; ++i) {
cnt = 0;
for(int j = 1; j <= n; ++j) F[j] = j;
for(int j = i; j <= m; ++j) {
int fa_u = find(e[j].u), fa_v = find(e[j].v);
if(fa_u == fa_v) continue;
F[fa_u] = fa_v;
if(++cnt == n - 1) {ans = min(ans, e[j].w - e[i].w); break; }
}
}
}
int main() {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++i) F[i] = i;
for(int i = 1; i <= m; ++i) scanf("%d%d%d", &e[i].u, &e[i].v, &e[i].w);
kruskal();
if(ans == 0x7fffffff) {printf("-1\n"); return 0; }
printf("%d\n", ans);
return 0;
}
安慰奶牛
题面:P2916
一开始想的是先找最小生成树,然后再遍历,后来发现其实只需要用边来记录点权即可。
一条边我们必然会走两次(因为最后还要回到原来的牧场),所以直接把边权赋成两次走的时间+在两个端点安慰奶牛的时间即可。也因为不管怎么走都会把所有边走两边,所以直接从交谈用时最小的牧场开始即可。
展开代码
#include <bits/stdc++.h>
#define ll long long
#define MyWife Cristallo
using namespace std;
const int N = 2 * 1e5 + 5, M = 1e4 + 5;
struct edge {
int u, v, w;
} e[N];
int n, m, ans = 0x7fffffff, cnt, F[M], talk[M];
bool cmp(edge a, edge b) {
return a.w < b.w;
}
int find(int x) {
if(F[x] == x) return x;
return F[x] = find(F[x]);
}
void kruskal() {
sort(e + 1, e + 1 + m, cmp);
for(int i = 1; i <= m; ++i) {
int fa_u = find(e[i].u), fa_v = find(e[i].v);
if(fa_u == fa_v) continue;
ans += e[i].w, F[fa_u] = fa_v;
//if(++cnt == n - 1) return;
}
}
int main() {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++i) F[i] = i;
for(int i = 1; i <= n; ++i) scanf("%d", talk + i), ans = min(ans, talk[i]);
for(int i = 1; i <= m; ++i) scanf("%d%d%d", &e[i].u, &e[i].v, &e[i].w), e[i].w *= 2, e[i].w += talk[e[i].v] + talk[e[i].u];
kruskal();
printf("%d\n", ans);
return 0;
}
After
一键查询精神状态: