【已补完】【解题报告】你非得用贪心解深搜题吗？——搜索题迷惑解法大赏

寒假 THOI 集训部分搜索题目（另类）题解

今日推歌：《カブってこうぜぇ feat.可不》-タケノコ少年

特别可爱的一个歌，，，

Before

集训时候做题做出的怪异解法和迷惑大赏，真实有用的成分低于迷惑成分

除了深搜以后（可能）还会有广搜题

本篇没有任何以贪心为正解的题，也（几乎）没有以正解做出来的题

如果接受↓

展开目录

目录

洛谷B3621 枚举元组

教练说是递归题，用 for 循环做不了，我不信，一定要用 for 循环做，于是有了以下乱搞做法：

思路

固定第一位，用 tot 数组来记录排列，从最后一位开始修改，当这一位超过 \(k\) 时，修改前一位，并把后面的位都改成 \(1\).

举个例子：【跳到代码】

\(n = 3,k = 2\)

初始：1 1 1
>输出
    ↓修改最后一位
1 1 2
>输出
    ↓如果修改，这一位将大于 k
1 1 2
  ↓修改上一位
1 2 2
    ↓将之后的位置都改成 1
1 2 1
>输出
    ↓修改最后一位
1 2 2
>输出
    ↓如果修改，这一位将大于 k
1 2 2
  ↓修改上一位
1 2 2
  ↓如果修改，这一位将大于 k
1 2 2
-下一层循环（修改首位）-
2 2 2
    ↓将之后的位置都改成 1
2 1 1
>输出
    ↓修改最后一位
2 1 2
>输出
    ↓如果修改，这一位将大于 k
2 1 2
  ↓修改上一位
2 2 2
    ↓将之后的都改成 1
2 2 1
>输出
    ↓修改最后一位
2 2 2
>输出
    ↓如果修改，这一位将大于 k
2 2 2
  ↓修改上一位
2 2 2
  ↓如果修改，这一位将大于 k
2 2 2
↓修改上一位
2 2 2
↓如果修改，这一位将大于 k
2 2 2
↓已是第一位
2 2 2
-退出循环-

缺点

从思路来看用递归更合适，但是我不太喜欢递归

用 for 模拟的话思维没有递归顺畅

而且 for 循环最多套到了四层（

AC代码

非正解，不建议学习

展开代码 
#include <bits/stdc++.h>
#define ll long long
#define MyWife Cristallo
using namespace std;
const int N = 1e5 + 5;
int n, k, tot[N], pos;
int main() {
	scanf("%d%d", &n, &k);
	for(int i = 1; i <= k; ++i) {
		for(int j = 1; j <= n; ++j) tot[j] = 1;
		// tot 数组：记录目前的排列
		tot[1] = i; // 首位固定
		for(int j = 1; j <= pow(k, n - 1); ++j) {
			// 首位固定，共有 pow(k, n - 1) 中排列
			for(int l = 1; l <= n; ++l) printf("%d ", tot[l]);
			++tot[n - pos]; // 修改这一位
			for(int l = 1; l <= n; ++l) {
				if(tot[n - l + 1] > k) {
					++tot[n - l]; // 如果这一位已经超过 k,修改上一位
					for(int m = n - l + 1; m <= n; ++m) tot[m] = 1;
					// 之后的都改成 1
				}
			}
			putchar('\n');
		}
	}
	return 0;
}

洛谷P2392 [保护当事人隐私]考前临时抱佛脚

image

贪心思路

直接看正解（并不

用 ls 和 rs 记录两个脑子的做题总量，如果 ls 大于等于 rs,就把当前用时最长的加到 rs,否则把用时最短的加到 ls.

结果：

image

DP思路

image

当我打出这句话后，我突然意识到：当时那道题是个 01 背包。

只要使左右脑中任一的工作时长最接近总时长的一半，用时就最短。所以做一个 01 背包，令 \(N = \displaystyle\sum\limits_{j=1}^{s_i}{a_{i,j}}^{}\),其中 \(i\) 代表当前是第几科,\(j\) 代表这是第几道题；背包的容量即为 \(\dfrac{N}{2}\).

其中每道题的重量和价值都是所花费的时间。

其实也很好理解，因为是要在时间小于等于总时间一半的情况下使时间最长。

四道题其实就是四个包，到时候把每个包的总时间加在一起就好了。

再看数据范围：

\[1\le s_i\le 20, \]

\[1\le a_{i,j} \le 60. \]

滚动数组啊 long long 啊什么的都不用开，可以直接上板子

这里写的滚动数组，因为我把每一科的题都压在一个二维背包里了（不用清空

虽然确实可以写三维，因为 \(5*25*1205 = 150625\) 也不大，但是丑（啊？

AC代码

展开代码 
#include <bits/stdc++.h>
#define ll long long
#define MyWife Cristallo
using namespace std;
//const int N = 1e5 + 5; 小朋友你小丑了
int s[5], a[5][25], dp[5][1205], sum, ans;
int main() {
	for(int i = 1; i <= 4; ++i) scanf("%d", s + i);
	for(int i = 1; i <= 4; ++i) {
		for(int j = 1; j <= s[i]; ++j) scanf("%d", a[i] + j), sum += a[i][j];
		for(int j = 1; j <= s[i]; ++j) for(int k = sum / 2; k >= a[i][j]; --k) dp[i][k] = max(dp[i][k], dp[i][k - a[i][j]] + a[i][j]);
		ans += sum - dp[i][sum / 2], sum = 0; // 多测要清空
//		cout << ans << endl;
	}
	printf("%d\n", ans);
	return 0;
}

提醒

多测不清空，亲人两行泪：

image

After

image

AcWing 165 小猫爬山

先给各位欣赏一下我的AcWing背景（

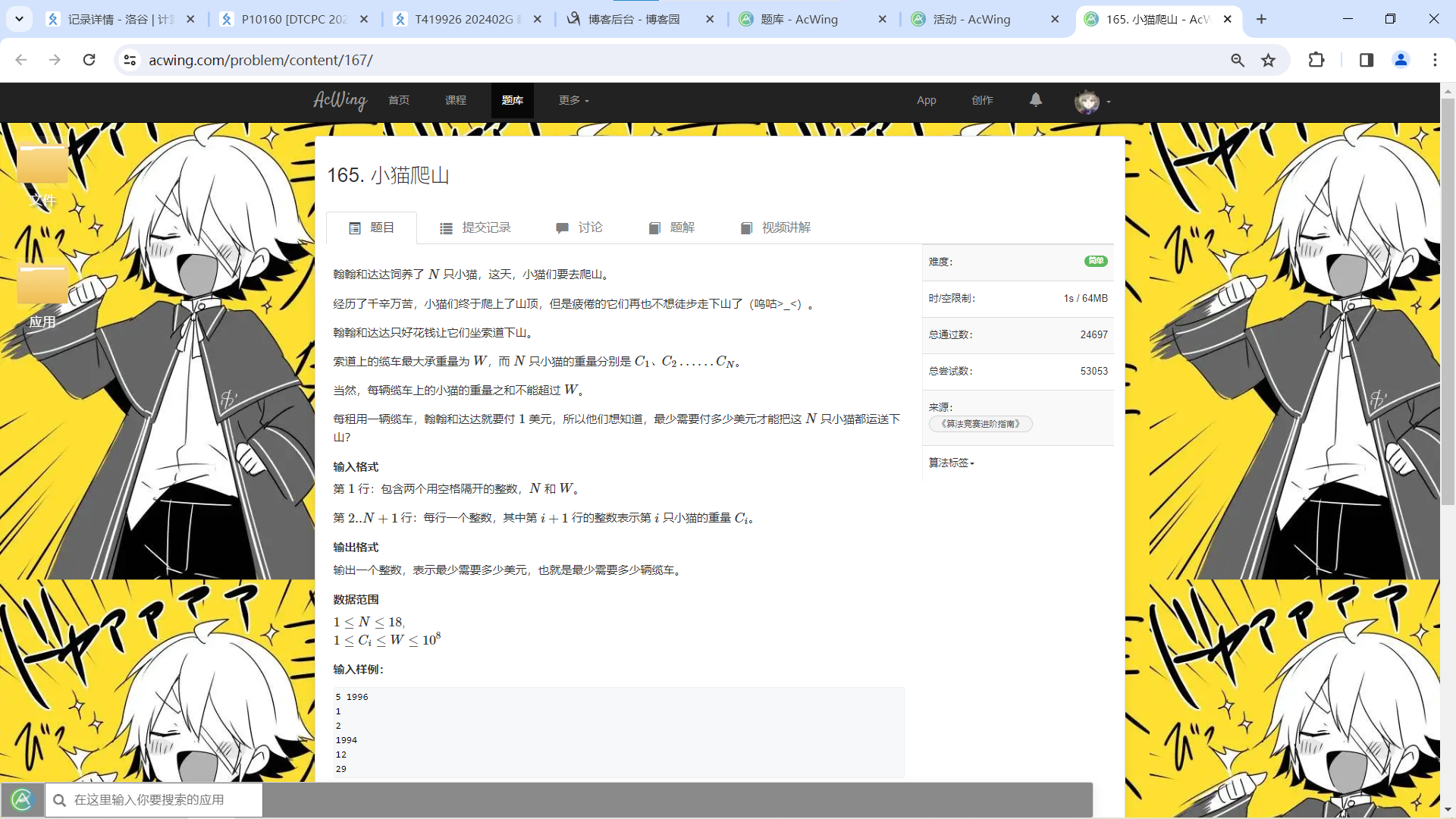
image

【跳到正解】

思路1

image

01 背包，用 vis 数组来记录一只小猫有没有下山

Then……

image

一维数组竟然 MLE 了！果然 \(1e8\) 的数据不应该乱开数组……

再看一眼：

image

这不是在卡我 01 背包是在干嘛？！

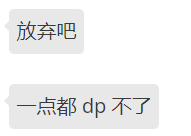
image

思路2

贪心，每次选能放进来的重量最大的猫

本着大胆尝试不予证明的原则，我们得到了这样的结果：

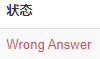
image

好吧，这下贪心也被 pass 了，只能爆搜了

思路3

DFS，据说这道题卡了很多东西所以要加很多剪枝，让我想起了一位哲人曾说过的话：

在天愿为比翼鸟，在地不愿做剪枝。

真是非常有哲理呢。

记录当前该第几个小猫上车，再枚举每个车，如果能放的下就继续 dfs 下一个小猫和这辆车，没有能放下的就再开一辆车。

需要注意的是因为记录的是当前该第一个小猫上车，所以当记录的参数等于 \(N\) 时这只小猫还没有上车呢（小猫：等等我！——

AC代码

展开代码 
#include <bits/stdc++.h>
#define ll long long
#define MyWife Cristallo
using namespace std;
//const int N = 1e5 + 5;
int n, w, c[25], v[25], ans = 18;
//bool vis[25];
void dfs(int ne, int k) {
//	if(vis[ne]) return;
	if(k > ans) return;
	if(ne > n) {ans = k; return; }
	for(int i = 1; i <= k; ++i) {
		if(v[i] + c[ne] > w) continue;
		v[i] += c[ne];
		dfs(ne + 1, k);
		v[i] -= c[ne];
	}
	v[++k] = c[ne];
	dfs(ne + 1, k);
	v[k] = 0;
}
int main() {
	scanf("%d%d", &n, &w);
	for(int i = 1; i <= n; ++i) scanf("%d", c + i);
	sort(c + 1, c + 1 + n, greater<int>());
	dfs(1, 1);
	printf("%d\n", ans);
	return 0;
}

After

image
image
image
image
image

洛谷 P1451 细胞数量

教练给的 bfs 题，所以我决定用 dfs 来解（啊？

阅读题面可知除了 \(0\) 都可以是细胞的一部分，所以可以遍历每个点，如果不是 \(0\),且不是其它细胞的一部分，就以这个细胞为起点遍历整个细胞，并使答案加 \(1\).

遍历细胞的过程并不是在寻找细胞的一部分，而是在排除不能成为下一个细胞一部分的部分。

AC代码

展开代码 
#include <bits/stdc++.h>
#define ll long long
#define MyWife Cristallo
using namespace std;
const int N = 1e5 + 5;
int n, m, ans;
char c[105][105];
bool vis[105][105];
void dfs(int x, int y) {
	if(vis[x][y]) return;
	if(c[x][y] == '0') return;
	if(x < 1 || y < 1 || x > n || y > m) return;
	vis[x][y] = 1;
	dfs(x - 1, y);
	dfs(x + 1, y);
	dfs(x, y - 1);
	dfs(x, y + 1);
}
int main() {
	scanf("%d%d", &n, &m); 
	getchar();
	for(int i = 1; i <= n; ++i) scanf("%s", c[i] + 1);
	for(int i = 1; i <= n; ++i) {for(int j = 1; j <= m; ++j) {if(c[i][j] != '0' && !vis[i][j]) {dfs(i, j); ++ans; } } } 
	printf("%d\n", ans);
	return 0;
}

After

image

image

洛谷 B3626 跳跃机器人

虽然是 bfs 题单里的，但是一眼普通递归。

如果目标是偶数的话直接跳 \(2x\) 肯定是最优的，如果是奇数的话跳到 \(x+1\) 或 \(x-1\) 再当作偶数处理，需要比较两种方式的优劣。

可以把路上的每一个点都当作一个单独的目标来考虑，注意判断是否出界。

AC代码

展开代码 
#include <bits/stdc++.h>
#define ll long long
#define MyWife Cristallo
using namespace std;
const int N = 1e5 + 5;
int n, now = 1, ans;
int dfs(int x) {
	if(x > n) return 0x7fffffff;
	if(x == 1) return 0;
	if(x % 2) return min(dfs(x - 1), dfs(x + 1)) + 1;
	return dfs(x / 2) + 1;
}
int main() {
	scanf("%d", &n);
	printf("%d\n", dfs(n));
	return 0;
}

After

image

洛谷 P5514 永夜的报应

一眼 Minus

异或有一个别称是“不进位的加法”，对于任意 \(a,b\),都有 \(a \oplus b \le a + b\).而且加法的结合律、交换律也对异或适用，所以我们可以得到

\[(a_1 \oplus a_2 \oplus a_3\oplus...\oplus a_n) + (a_{n+1} \oplus a_{n + 2} \oplus a_{n + 3} \oplus ... \oplus a_{2n}) \ge a_1 \oplus a_2 \oplus a_3 \oplus ... \oplus a_{2n} \]

所以把所有数分到一组为最优，得到代码：

展开代码 
#include <bits/stdc++.h>
#define ll long long
#define MyWife Cristallo
using namespace std;
const int N = 1e6 + 5;
int n, a, ans;
int main() {
	scanf("%d", &n);
	for(int i = 1; i <= n; ++i) scanf("%d", &a), ans ^= a;
	printf("%d\n", ans);
	return 0;
}

After

image

等等这题和搜索有啥关系啊，难道大家都是硬搜的吗

哦今天学进制转换了

结语（正文还没有结束……！）

其实我不喜欢搜索主要是我递归回溯的时候总是弄不明白该在什么时候回溯、怎么回溯……甚至超过了我怕dp的程度

不过除了刻意卡（小猫爬山……）之外真的不能用别的方法解的搜索题吗……？于是我写了这玩意。

image

posted @ 2024-02-18 21:53  _Kiichi  阅读(81)  评论(5)  编辑  收藏  举报