2024.09 别急记录
1. ARC070F - HonestOrUnkind
发现
维护一个栈表示目前越来越好的人,每次取出栈顶询问新人,若为好则将新人放入栈顶;否则将栈顶弹出。最后栈顶一定是一个好人,让他询问一遍所有人即可。
点击查看代码
//AT_arc070_d #include <bits/stdc++.h> using namespace std; int qry(int x, int y){ if(x == y){ return 1; } printf("? %d %d\n", x, y); fflush(stdout); char s[4]; scanf("%s", s); return s[0] == 'Y'; } int st[4010]; int main(){ int n, a, b; scanf("%d%d", &a, &b); if(a <= b){ puts("Impossible"); fflush(stdout); return 0; } n = a + b; int tp = 0; for(int i = 0; i < n; ++ i){ if(tp == 0){ st[++tp] = i; } else { if(qry(st[tp], i)){ st[++tp] = i; } else { -- tp; } } } int x = st[tp]; for(int i = 0; i < n; ++ i){ st[i] = qry(x, i); } putchar('!'); putchar(' '); for(int i = 0; i < n; ++ i){ putchar(st[i] + '0'); } puts(""); return 0; }
2. CF843E - Maximum Flow
考虑答案(满流边)相当于一个全部由 1 边组成的割,那么这个最小割是好求的:对于 0 边连
求得最小割以后把所有 1 边加入图中跑流量
点击查看代码
//CF843E #include <bits/stdc++.h> using namespace std; const int N = 110, M = 1e5 + 10, inf = 1000; int n, m, s, t, mc[M], deg[N]; struct edge{ int u, v, g; } E[M]; int hd[N], now[N], dep[N], ln[M], eg[M], nx[M], tot = 1; void adg(int u, int v, int w){ eg[++tot] = v; ln[tot] = w; nx[tot] = hd[u]; hd[u] = tot; } void add(int u, int v, int w, int ww){ adg(u, v, w); adg(v, u, ww); } bool bfs(int s, int t){ memset(dep, 0, sizeof(dep)); memcpy(now, hd, sizeof(hd)); queue<int> q; dep[s] = 1; q.push(s); while(!q.empty()){ int x = q.front(); q.pop(); for(int i = hd[x]; i; i = nx[i]){ int y = eg[i], z = ln[i]; if(z && !dep[y]){ dep[y] = dep[x] + 1; q.push(y); if(y == t){ return 1; } } } } return 0; } int dfs(int x, int t, int fl){ if(x == t){ return fl; } int rs = fl; for(int i = now[x]; i && rs; i = nx[i]){ int y = eg[i], z = ln[i]; now[x] = i; if(z && dep[y] == dep[x] + 1){ int k = dfs(y, t, min(z, rs)); if(!k){ dep[y] = 0; } ln[i] -= k; ln[i^1] += k; rs -= k; } } return fl - rs; } int dinic(int s, int t){ int mf = 0, tmp; while(bfs(s, t)){ while(tmp = dfs(s, t, inf)){ mf += tmp; } } return mf; } int main(){ scanf("%d%d%d%d", &n, &m, &s, &t); for(int i = 1; i <= m; ++ i){ scanf("%d%d%d", &E[i].u, &E[i].v, &E[i].g); if(E[i].g){ add(E[i].u, E[i].v, 1, inf); } else { add(E[i].u, E[i].v, inf, 0); } } printf("%d\n", dinic(s, t)); bfs(s, t); for(int i = 1; i <= m; ++ i){ if(dep[E[i].u] && !dep[E[i].v] && E[i].g){ mc[i] = 1; } } tot = 1; memset(hd, 0, sizeof(hd)); for(int i = 1; i <= m; ++ i){ if(E[i].g){ add(E[i].u, E[i].v, inf, 0); ++ deg[E[i].v]; -- deg[E[i].u]; } else { tot += 2; } } int S = n + 1, T = n + 2; for(int i = 1; i <= n; ++ i){ if(deg[i] > 0){ add(S, i, deg[i], 0); } if(deg[i] < 0){ add(i, T, -deg[i], 0); } } add(t, s, inf, 0); dinic(S, T); for(int i = 1; i <= m; ++ i){ if(E[i].g){ int k = ln[i*2+1] + 1; printf("%d %d\n", k, k + 1 - mc[i]); } else { puts("0 1"); } } return 0; }
3. 「C.E.L.U-02」 - 苦涩
首先考虑线段树每个节点维护一个堆+区间内 max(不一定是真实的),然后每次添加往 log 个区间内加数(所以需要标记永久化,所以区间 max 不一定是真的),查询是简单的,但是需要使区间堆顶也贡献(区间堆顶=每个片区都有;区间 max=只有一个片区有。两个不同)。修改的时候暴力递归,遇到堆顶=需要删掉的数时将区间与操作区间补集交集的部分递归下去改即可。因为加的区间不多,所以删的也不会多。总复杂度
点击查看代码
//P7476 #include <bits/stdc++.h> using namespace std; const int N = 2e5 + 10; int n, m; struct node{ int mx; priority_queue<int> q; } t[N*8]; void psu(int p){ t[p].mx = max({ t[p<<1].mx, t[p<<1|1].mx, t[p].q.top() }); } void add(int p, int l, int r, int ql, int qr, int v){ if(qr < l || r < ql){ return; } else if(ql <= l && r <= qr){ t[p].mx = max(t[p].mx, v); t[p].q.push(v); } else { int mid = l + r >> 1; add(p<<1, l, mid, ql, qr, v); add(p<<1|1, mid+1, r, ql, qr, v); psu(p); } } void psd(int p, int l, int r, int ql, int qr, int v){ if(ql <= l && r <= qr){ return; } int mid = l + r >> 1; if(ql > mid){ t[p<<1].mx = max(t[p<<1].mx, v); t[p<<1].q.push(v); psd(p<<1|1, mid+1, r, ql, qr, v); } else if(qr <= mid){ t[p<<1|1].mx = max(t[p<<1|1].mx, v); t[p<<1|1].q.push(v); psd(p<<1, l, mid, ql, qr, v); } else { psd(p<<1, l, mid, ql, qr, v); psd(p<<1|1, mid+1, r, ql, qr, v); } psu(p); } void del(int p, int l, int r, int ql, int qr, int v){ if(qr < l || r < ql || t[p].mx < v){ return; } else if(t[p].q.top() == v){ t[p].q.pop(); psd(p, l, r, ql, qr, v); psu(p); } else { int mid = l + r >> 1; del(p<<1, l, mid, ql, qr, v); del(p<<1|1, mid+1, r, ql, qr, v); psu(p); } } int qry(int p, int l, int r, int ql, int qr){ if(qr < l || r < ql){ return -1; } else if(ql <= l && r <= qr){ return t[p].mx; } else { int mid = l + r >> 1; return max({ qry(p<<1, l, mid, ql, qr), qry(p<<1|1, mid+1, r, ql, qr), t[p].q.top() }); } } int main(){ scanf("%d%d", &n, &m); for(int i = 0; i < N*4; ++ i){ t[i].q.push(-1); t[i].mx = -1; } for(int i = 1; i <= m; ++ i){ int op, l, r, k; scanf("%d%d%d", &op, &l, &r); if(op == 1){ scanf("%d", &k); add(1, 1, n, l, r, k); } else if(op == 2){ int p = qry(1, 1, n, l, r); if(p != -1){ del(1, 1, n, l, r, p); } } else { printf("%d\n", qry(1, 1, n, l, r)); } } return 0; }
4. CF1009F - Dominant Indices
有 dp 式:
解决“直接继承”的方法是开一个 *f[N],buf[N] 然后每次遍历到节点将 buf 中一个连续的
点击查看代码
//CF1009F #include <bits/stdc++.h> using namespace std; const int N = 1e6 + 10; int n, dep[N], mx[N], son[N]; int buf[N*2], ans[N], *f[N], *now = buf; vector<int> g[N]; void dfs(int x, int fa){ mx[x] = dep[x] = dep[fa] + 1; for(int i : g[x]){ if(i != fa){ dfs(i, x); if(mx[i] > mx[x]){ son[x] = i; mx[x] = mx[i]; } } } } void calc(int x){ f[x][0] = 1; if(son[x]){ f[son[x]] = f[x] + 1; calc(son[x]); ans[x] = ans[son[x]] + 1; } for(int y : g[x]){ if(y == son[x] || dep[y] < dep[x]){ continue; } f[y] = now; now += mx[y] - dep[y] + 1; calc(y); for(int i = 1; i <= mx[y] - dep[y] + 1; ++ i){ f[x][i] += f[y][i-1]; if(f[x][i] > f[x][ans[x]] || (f[x][i] == f[x][ans[x]] && i < ans[x])){ ans[x] = i; } } } if(f[x][ans[x]] == 1){ ans[x] = 0; } } int main(){ scanf("%d", &n); for(int i = 1; i < n; ++ i){ int x, y; scanf("%d%d", &x, &y); g[x].push_back(y); g[y].push_back(x); } dfs(1, 0); f[1] = now; now += mx[1] - dep[1] + 1; calc(1); for(int i = 1; i <= n; ++ i){ printf("%d\n", ans[i]); } return 0; }
5. AHOI2022 - 山河重整
首先有显然的
那么这个感觉不好优化。考虑容斥。设
转移为
考虑
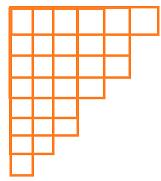
容易发现列数为
for(int i = sqrt(n * 2) + 3; i >= 1; -- i){ for(int j = n; j >= i; -- j){ g[j] = g[j-i]; } upd(g[i], 1); for(int j = i; j <= n; ++ j){ upd(g[j], g[j-i]); } } g[0] = 1;
接下来设
- 遍历每一行方格数
- 必须有一个
- 对于
- 更新。
最后用
点击查看代码
//P8340 #include <bits/stdc++.h> using namespace std; const int N = 5e5 + 10; int n; typedef long long ll; int f[N], P, pw[N], g[N]; void upd(int &x, int y){ x += y; if(x >= P){ x -= P; } } void calc(int n){ if(n <= 1){ return; } calc(n >> 1); memset(g, 0, sizeof(g)); for(int i = sqrt(n * 2) + 3; i >= 1; -- i){ for(int j = n; j >= i; -- j){ g[j] = g[j-i]; } for(int j = 0; i*(j+2)+j <= n; ++ j){ upd(g[i*(j+2)+j], f[j]); } for(int j = i; j <= n; ++ j){ upd(g[j], g[j-i]); } } for(int i = (n >> 1) + 1; i <= n; ++ i){ upd(f[i], P - g[i]); } } int main(){ scanf("%d%d", &n, &P); pw[0] = 1; for(int i = 1; i <= n; ++ i){ upd(pw[i], pw[i-1]); upd(pw[i], pw[i-1]); } for(int i = sqrt(n * 2) + 3; i >= 1; -- i){ for(int j = n; j >= i; -- j){ f[j] = f[j-i]; } upd(f[i], 1); for(int j = i; j <= n; ++ j){ upd(f[j], f[j-i]); } } f[0] = 1; calc(n); int ans = 0; for(int i = 0; i < n; ++ i){ upd(ans, (ll)f[i] * pw[n-i-1] % P); } printf("%d\n", (pw[n] + P - ans) % P); return 0; }
6. JOISC 2022/2023 - Two Currencies
将每条路径绑定到更深的节点上,使用可持久化线段树维护每个节点到根路径所有银币数,查询则在
点击查看代码
//qoj6332 #include <bits/stdc++.h> using namespace std; const int N = 1e5 + 10; typedef long long ll; int n, m, q, p[N], c[N], to[N], fat[N][20], dep[N], cnt, rt[N]; vector<pair<int, int> > g[N]; pair<int, int> cc[N]; vector<int> cp[N]; struct node{ ll val; int sum, l, r; } t[N*40]; void upd(int p){ t[p].val = t[t[p].l].val + t[t[p].r].val; t[p].sum = t[t[p].l].sum + t[t[p].r].sum; } void add(int &p, int l, int r, int x, ll v){ ++ cnt; t[cnt] = t[p]; p = cnt; if(l == r){ t[p].val += v; ++ t[p].sum; } else { int mid = l + r >> 1; if(x <= mid){ add(t[p].l, l, mid, x, v); } else { add(t[p].r, mid+1, r, x, v); } upd(p); } } int qx(int px, int py, int pz, int l, int r, ll y){ if(l == r){ return l; } else { int mid = l + r >> 1; ll val = t[t[px].l].val + t[t[py].l].val - 2 * t[t[pz].l].val; if(val > y){ return qx(t[px].l, t[py].l, t[pz].l, l, mid, y); } else { return qx(t[px].r, t[py].r, t[pz].r, mid+1, r, y-val); } } } int qy(int px, int py, int pz, int l, int r, int ql, int qr){ if(qr < l || r < ql){ return 0; } else if(ql <= l && r <= qr){ return t[px].sum + t[py].sum - 2 * t[pz].sum; } else { int mid = l + r >> 1; return qy(t[px].l, t[py].l, t[pz].l, l, mid, ql, qr) + qy(t[px].r, t[py].r, t[pz].r, mid+1, r, ql, qr); } } void pre(int x, int fa){ fat[x][0] = fa; for(int i = 1; i < 20; ++ i){ fat[x][i] = fat[fat[x][i-1]][i-1]; } dep[x] = dep[fa] + 1; for(auto i : g[x]){ if(i.first == fa){ continue; } to[i.second] = i.first; pre(i.first, x); } } int lca(int x, int y){ if(dep[x] > dep[y]){ swap(x, y); } for(int i = 19; i >= 0; -- i){ if(dep[fat[y][i]] >= dep[x]){ y = fat[y][i]; } } if(x == y){ return x; } for(int i = 19; i >= 0; -- i){ if(fat[x][i] != fat[y][i]){ x = fat[x][i]; y = fat[y][i]; } } return fat[x][0]; } void dfs(int x){ for(auto i : g[x]){ int y = i.first; if(y == fat[x][0]){ continue; } rt[y] = rt[x]; for(int j : cp[y]){ add(rt[y], 1, m+1, j, cc[j].first); } dfs(y); } } int main(){ scanf("%d%d%d", &n, &m, &q); for(int i = 1; i < n; ++ i){ int x, y; scanf("%d%d", &x, &y); g[x].emplace_back(y, i); g[y].emplace_back(x, i); } pre(1, 0); for(int i = 1; i <= m; ++ i){ scanf("%d%d", &p[i], &c[i]); cc[i] = make_pair(c[i], i); } sort(cc + 1, cc + m + 1); for(int i = 1; i <= m; ++ i){ c[i] = lower_bound(cc + 1, cc + m + 1, make_pair(c[i], i)) - cc; cp[to[p[i]]].push_back(c[i]); } add(rt[1], 1, m+1, m+1, 1e18); dfs(1); while(q--){ int s, t, x; ll y; scanf("%d%d%d%lld", &s, &t, &x, &y); int pos = qx(rt[s], rt[t], rt[lca(s, t)], 1, m+1, y); int ans = qy(rt[s], rt[t], rt[lca(s, t)], 1, m+1, pos, m+1); printf("%d\n", max(-1, x - ans)); } return 0; }
7. CF1884E - Hard Design
第一问简单;第二问相当于要求
点击查看代码
//CF1884E #include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = 2e6 + 10; const ll P = 1e9 + 7; ll pr[N], sf[N], ans[N], sm, a[N], mx; int st[N], cnt[N], tp; int T, n, ps; int main(){ scanf("%d", &T); while(T--){ mx = ps = sm = 0; scanf("%d", &n); for(int i = 1; i <= n; ++ i){ scanf("%lld", &a[i]); a[i+n] = a[i]; if(a[i] > mx){ mx = a[i]; ps = i; } sm += a[i]; } sm %= P; ll tmp = 0; tp = 0; for(int i = ps + 1; i <= ps + n; ++ i){ int tc = 1; while(tp && a[st[tp]] <= a[i]){ tc += cnt[tp]; tmp = (tmp + P - a[st[tp]] * 1ll * cnt[tp] % P) % P; -- tp; } st[++tp] = i; cnt[tp] = tc; tmp = (tmp + a[st[tp]] * 1ll * cnt[tp]) % P; pr[i] = (pr[i-1] + tmp) % P; } tmp = tp = 0; for(int i = 0; i <= n+n; ++ i){ cnt[i] = st[i] = 0; } for(int i = ps + n; i >= ps + 1; -- i){ int tc = 1; while(tp && a[st[tp]] <= a[i]){ tc += cnt[tp]; tmp = (tmp + P - a[st[tp]] * 1ll * cnt[tp] % P) % P; -- tp; } st[++tp] = i; cnt[tp] = tc; tmp = (tmp + a[st[tp]] * 1ll * cnt[tp]) % P; sf[i] = (sf[i+1] + tmp) % P; ans[i] = (sf[i] + pr[i-1] + mx * 1ll * (i-ps-1) % P * (n-i+ps+1)) % P; if(i - n >= 1){ ans[i-n] = ans[i]; } } ll sum = 0; #define cal(i) max(0ll, a[i-1]-a[i]) for(int i = 1; i < n; ++ i){ sum += cal(i); } for(int i = 1; i <= n; ++ i){ sum -= cal(i); sum += cal(i+n-1); ll rs = (mx * 1ll * n % P * n % P + P + P - ans[i] - ans[i] + sm) % P; printf("%lld %lld\n", sum + mx - a[i], rs); } for(int i = 0; i <= n+n; ++ i){ pr[i] = sf[i] = ans[i] = a[i] = st[i] = cnt[i] = 0; } } return 0; }
8. CF1622F - Quadratic Set
答案
于是可以利用哈希判定是否存在




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步