「比赛」abc 262

E - Red and Blue Graph
算是一眼秒的。

第一感觉是有可能和图长什么样没有关系。

发现重要信息：「偶数」。想到异或起来为 \(0\)。发现 “两个端点颜色不同”也可以转化为异或。

于是本题只和度数有关。简单排列组合即可。

---

F - Erase and Rotate
思路不难，细节有一些。

考虑第一位是什么，于是可以刚开始就考虑操作 \(2\)，后面只考虑操作 \(1\)。

注意后面使用了操作 \(2\) 的数，可以“免去”操作 \(1\) 的代价。

于是用一个栈维护贪心即可。

注意有两种情况：不用操作二和用操作二。

---

(*)Ex - Max Limited Sequence
弱化条件：所有 \(X\) 都相等

令 \(dp_{i,j}\) 为当前填到第 \(i\) 个位置，选的最近的 \(X\) 位置为 \(j\) 的方案数。√

令 \(dp_i\) 为选到 \(i\) 合法的方案数 ×，因为中间的限制我们就不方便囊括了。

简单 dp 即可。发现直接在 \(dp_j\) 这个数组上做修改即可。用个前缀和/滑动窗口（two-pointers），是 \(\mathcal O(n)\) 的。

回到原题面。考虑和刚才的差别在哪？一个限制会受另一个限制的影响。就是说，下图。

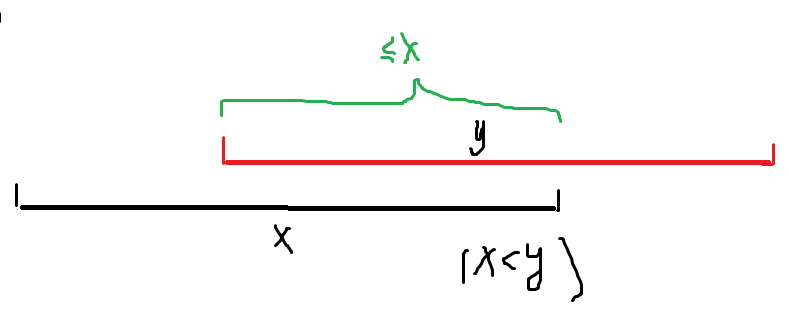
所以，我们能不能消去这种限制？令 \(b_i\) 为满足所有限制，\(a_i\) 取到的上界。发现如果有一个限制包括了它，但是 \(X>b_i\)，那么 \(i\) 肯定不能对这个限制产生影响，所以不用考虑它了。所以我们把 \(b_i\) 和 \(X\) 相同的单独拎出来，做一遍刚才的操作，最后乘法原理合并即可。

复杂度：\(\mathcal {O(n\log_2n)}\)。