2022.7.26 模拟赛
T1
link
（大）模拟。。。
打了 1h，调了很久。。。
我觉得应该一句一句读，可以高亮标记一下。。。
坑点：
- 会有负数，所以向下取整不能 “/2”。
- 输出注意 “0”。
T2
（SPJ）
乱打的。。。过了。。。原来是《签到题》啊。
充分发挥人类智慧。发现 gggg...zzzz..g/z 似乎是正确的。当然更 nb 的，可以将认为合理的都试一次。
证明：其实也很显然（？）。这里先咕了。
出题人还是挺厉害的。
但如果 \(n\) 小也可以差分约束。不知道本题使用 spfa 优化的差分约束复杂度是不是正确的。
T3
个人认为也是一道好题。（至少比较妙）
发现一个性质：如果一个数比上一个数小，那么在没有其他限制的条件下，它可以取 \(1\)。这就给了我一个启示：dp，从左到右跑一遍看左边比右边小的情况，从右到左看右边比左边的小的情况即可。
先证合法：想一想发现肯定合法，懒得写了（/xyx）
再证最优：发现每个数都是它能取到的最优情况，所以肯定最优（/xyx）
T4
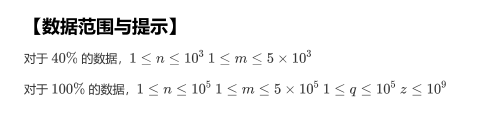
也是一道好题。
考虑肯定是对于 \(dis(x,y)\)，找出 \(x,y\) 到 \(1\) 之间路径的交，令其中一个点为 \(z\)，则 \(dis(x,y)=\min\{dis(x,z)+dis(y,z)\}\)。
然后现在要快速找到 \(x\) 到它祖先的最短路。
考场上的想法是对于每个点直接找到它到 \(1\) 节点路径上所有的边，然后每次跑 dijkstra 不会 T？应该想清楚一点的。。
发现对于每一条边只会被存在于 \(20\) 次 dijkstra 中，所以其实时间复杂度是 \(\mathcal {O}(20mlog_2m)\) 的。还有就是 \(dis[x][y]\) 改成 map，但还是一个 \(\log\)，因为这两个 \(\log\)
是独立的。
实现改成对子树操作，发现找祖先在某种意义上就等于找子树啊。。好打多了。
