2022.7.22 模拟赛
Pro 1
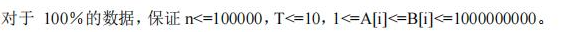
经典贪心，列出 \(1\) 在 \(2\) 前，和 \(2\) 在 \(1\) 前的条件，发现可以比较。
Pro 2
我先猜它是个单峰函数。
单峰函数交单峰函数还是单峰，所以证完了。
但是有 \(\mathcal {O}(n)\) 的做法：
首先 \(|sum|\) 最大可以转化为 \(\max \{pre_i\}-\min \{pre_i\}\)，这一步就是一个 trick 了。
然后可以把前缀和看成 \(n\) 个，函数，\(x\) 为自变量，\(pre_i+ix\) 为因变量，是个一次函数。发现可以用单调栈维护。然后比较显然，只会在两个函数交替的端点处取得最大值/最小值，所以可以 \(\mathcal {O(n)}\)。
这个做法是学习的 这篇博客
Pro 3
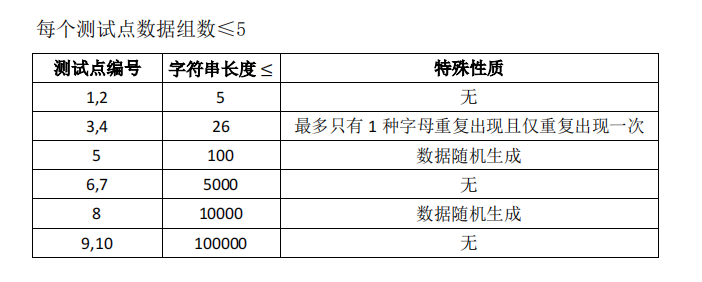
回文的重要性质：固定中间点，长度具有单调性。
再用常见 trick，每两个之间填一个相同的奇怪的字符。
这样做可以将所有回文串长度转化为奇数，然后得到一些区间做经典贪心即可。
Pro 4
题比较好。
显然是 ST 表找出奇偶性与左端点相同的，不为右端点的，最小的数。再找它右边奇偶性与它不同的最小的数。找到这样一对数后将区间分成 \(3\) 份，递归求解便可以将所有的数匹配。
考虑如何组合。发现必须选了一些数后才能选另一些数。可以用启发式合并，这样不容易错。否则我们将限制关系建成一个 DAG（其实是一棵树），然后拓扑排序+优先队列即可。
注意 1（！！）：建限制关系必须是被限制指向限制的（因为要求字典序），不能反着来。否则我们只能得到倒着的字典序最大，却不能得到正着的字典序最小。
例子：3->4 5->2.
此题可以和 「HNOI2015」菜肴制作 一起辩证看待。
注意 2（！！）：本来建限制关系只用建它和它的内部，但注意这个限制关系不仅仅是儿子父亲的关系，这个点会受到它的子树所有节点的限制。而我们这样建图只能连到一条链（即一直往内部走），其他节点并不在树上。如果硬要拓扑，解决方法是：一个点向它直接儿子的左右也连边。
也可以采用更好写的：一个点直接向它的左右连边。考虑这样满足它、左、右奇偶性相同，而它的数最小，所以其实它其实不会被左右限制。
