题解 CF1521E Nastia and a Beautiful Matrix

link
比较经典的构造题。（真的就是 构造 题）
先考虑我们最多能填多少数，构造一波，发现可以：

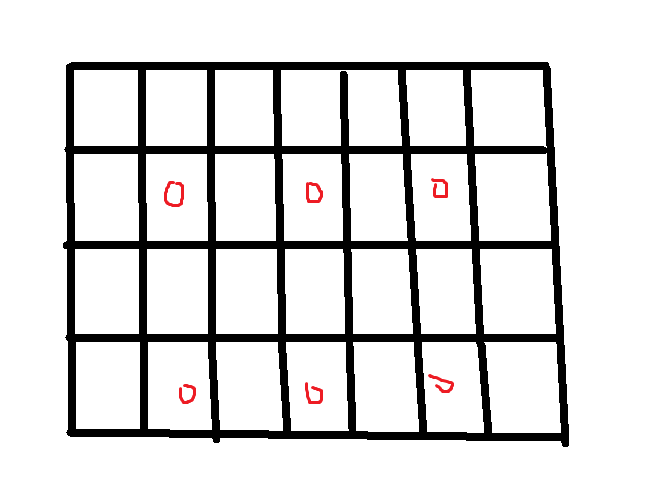
即有值的位置的个数 \(\leqslant n^2-\lfloor \frac n 2 \rfloor ^ 2\)，但是如果这些数都相同，肯定是不行了。那么我们可以考虑一个相同的数最多可以出现多少次。
我们又构造一波，发现这个次数 \(\leqslant n \lceil \frac n 2 \rceil\)。我们大概猜测出现最大次数 \(\leqslant n \lceil \frac n 2 \rceil\) 时必定有解，让我们来构造。发现直接构不好做。那让我们转化一下：选定一个顺序依次填数（数相等的相邻填），使得不能相等的两个位置填数的时间戳差值 \(> n \lceil \frac n 2 \rceil\)。（其实是使条件限制得更死了）
一个比较显然的思路是:

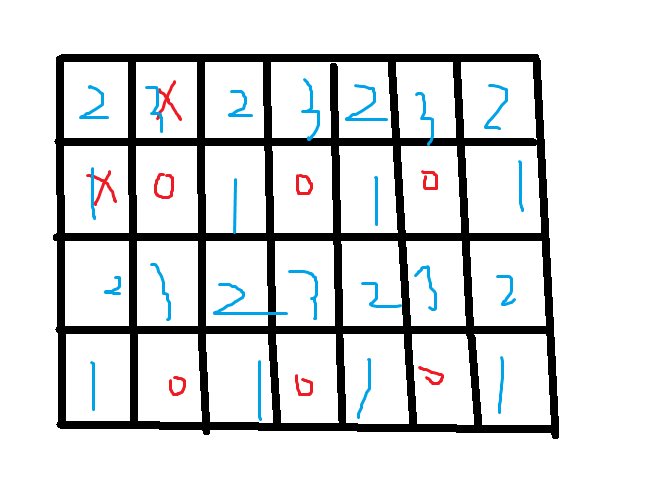
按照这个顺序填，但明显用于缓冲的 \(2\) 只有 \(\lceil \frac n 2 \rceil ^ 2\) 个，不满足我们的要求。怎么办！！！
考虑按照这种顺序填数不合法只能是 \(1\) 和 \(3\) 的某两个位置发生冲突。也就是说，尽可能避免一个数贯穿了 \(2\)。所以考虑将数的数量从大到小排序。又来分讨大法。
若数量最多的数进入了 \(2\)（但不可能超过 \(2\)），那么 \(1\) 和 \(3\) 不可能出现相同的。
若数量最多的数在 \(1\) 中戛然而止（只能指声音（雾）），那么所有数的数量 \(\leqslant \lceil \frac n 2 \rceil ^ 2\)，自然 \(1\) 和 \(3\) 也不可能出现相同的。
至于为什么想到按数量排序，我们肯定想刚开始的 \(\lceil \frac n 2 \rceil ^ 2\) 个不能白费了。。（
本题还是如果稍微不相信自己的做法就会直接弃掉，要敢于钻研！（）（）（）