题解 CF196E Opening Portals'
link
本题最小生成树不难看出，瓶颈在他们之间边怎么连，这应该是个完全图啊。
能不能从原图的边入手呢？发现原图的边可以充当我们新建图的边（trick）。具体地，令 \(x-y\) 为原图的边，离 \(x\) 最近的传送门为 \(s\)，\(y\) 最近的为 \(t\)，则建 \(s-t\)，边权为 \(dist(x,s)+dist(y,t)+dist(x,y)\)。
一个最大的疑惑是为什么只用找最近的传送门。考虑一个性质：如果路径 \(s-t\) 在一个环中，环中其他边的权值都比他大，那么这条边一定不在 mst 中。我们可以利用这个性质证明。
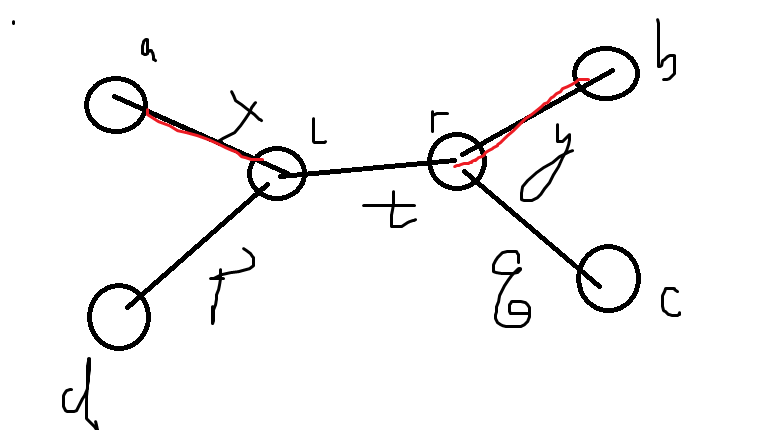
其中，离 \(l\) 最近的传送门为 \(a\)，\(r\) 的为 \(b\)。因此有 \(x<p,y<q,x<t+q,x<t+y,y<t+p,y<t+x\)。
那么我们将 \(a-b\)，现在要证为什么不连 \(a-c\ /\ d-b\ /\ d-c\)。
- 不连 \(d-c\)。
发现 \(a\sim d, d\sim c, c \sim a\) 形成一个环，而 \(d\sim c\) 是最大的路径，于是不可能成为边。 - 不连 \(a-c\)。
发现 \(a\sim b, b\sim c, c \sim a\) 形成一个环，而 \(a\sim c\) 是最大的路径，于是不可能成为边。 - 不连 \(d-b\)。
发现 \(d\sim a, a\sim b, d \sim b\) 形成一个环，而 \(d\sim b\) 是最大的路径，于是不可能成为边。
最后跑一遍 mst，注意把 \(1\) 也和他们连接起来（和传送门的最短路径）。
