「多校联训」I Love Random
可以说是一种dp的思维技巧
Problem
给定一个排列 \(p\),你可以智慧地按顺序选择多个区间使这个区间的每个数都等于这个区间的最小值。问最后能得到多少个不同的排列,答案对 \(10^9+7\) 取模。(\(len_p \le 5000\))
Solution
起初我想了一个区间 dp,想必也是大众容易想到的。对于区间 \([l,r]\),找到其中最小值所在的位置 \(k\)。然后枚举 \(k\) 能覆盖到的区间,前缀和优化是 \(\mathcal {O}(n^2log_2n)\) 的。
但是这样做会有一个很大的问题:
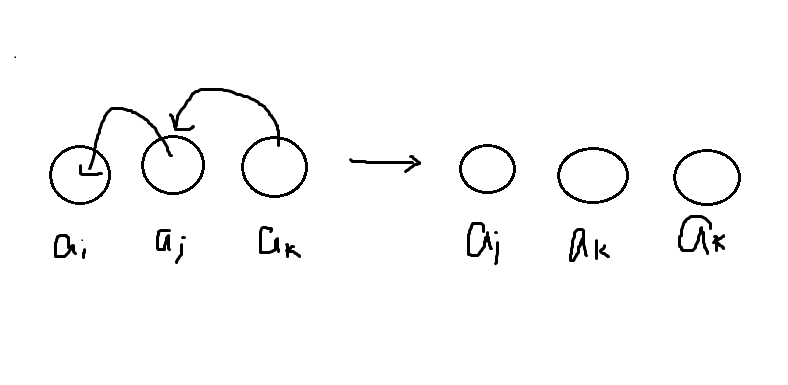
如图,\(a_i>a_j>a_k\),当我们考虑 \(dp[i][k]\) 的转移时枚举到 \(j\),我们用到的是 \(dp[i][j-1]\),但是这显然没有图中这种情况。
既然考虑原序列有后效性的话,考虑直接构造答案序列。
具体地,令 \(dp[i][j]\) 表示考虑获得了长度为 \(i\) 的答案序列,第 \(i\) 个值为 \(p_j\) 的方案总数。
这样的话,转移就很简单了(其实也不简单)。
首先用一个通用套路,考虑 \([L_i,R_i]\) 为 \(p_i\) 能修改到的范围。令最后的答案序列为 \(\{a\}\)。令 \(a_{i-1}=k\)。令 \(a_i=t\)。
读者容易证明这里答案下标是单调递增的。换句话说,只要保证 \(\forall L[t] \le i \le R[t]\),且其单增,这种方案一定合法。所以直接转移就可以啦~
于是好像就做完了,\(L、R\) 数组暴力就可以搞出来。
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <iostream>
#define LL long long
#define uint unsigned int
using namespace std;
const int MAXN = 5e3 + 5, Mod = 1e9 + 7;
#define Debug(x) cerr << #x << ' ' << x
#define hh cerr << endl
int n, a[MAXN], L[MAXN], R[MAXN], dp[2][MAXN], res;
int Qplus(int x, int y) { return x + y >= Mod ? x + y - Mod : x + y; }
int main() {
// freopen("C.in", "r", stdin);
// freopen("C.out", "w", stdout);
scanf("%d", &n);
for(int i = 1; i <= n; i ++) scanf("%d", &a[i]);
for(int i = 1; i <= n; i ++) {
for(int j = i; j >= 1; j --) if(a[j] < a[i]) { L[i] = j + 1; break; }
if(!L[i]) L[i] = 1;
for(int j = i + 1; j <= n; j ++) if(a[j] < a[i]) { R[i] = j - 1; break; }
if(!R[i]) R[i] = n;
}
for(int i = 1; i <= n; i ++) if(L[i] == 1) dp[1][i] = 1;
for(int i = 2; i <= n; i ++) {
bool f = (i & 1); int tmp = 0;
for(int j = 1; j <= n; j ++) dp[f][j] = 0; // 滚动数组清零(
for(int j = 1; j <= n; j ++) {
tmp = Qplus(tmp, dp[f ^ 1][j]);
if(L[j] <= i && R[j] >= i) dp[f][j] = Qplus(dp[f][j], tmp);
}
}
for(int i = 1; i <= n; i ++) res = Qplus(res, dp[n & 1][i]);
printf("%d", res);
return 0;
}
这就告诉我们察觉出dp状态有无后效性,和发现了后效性怎么换状态。/emm
同样的题

考虑一般的区间dp也会有后效性,这时考虑dp转移答案序列。
令 \(dp[i][j][k][\{0,1,2\}]\) 表示考虑答案序列的前 \(i\) 位,放了 \(j\) 个 \(G\),\(k\) 个 \(Y\),\(i-j-k\) 个 \(R\) 的方案总数。考虑最后需要移动的次数为下标的逆序对个数,所以直接转移即可((
另,这种题要想好了再打。把逻辑理清,不要慌。
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <iostream>
#define LL long long
#define uint unsigned int
using namespace std;
#define Debug(x) cerr << #x << ' ' << x
#define hh cerr << endl
const int MAXN = 405, inf = 0x3f3f3f3f;
int n, dp[2][MAXN][MAXN][3], a[MAXN], g[3], c[3][MAXN], res = inf;
int pre[3][MAXN];
char s[MAXN];
// dp[][][][f]
int Max(int x, int y) { return x > y ? x : y; }
int Min(int x, int y) { return x < y ? x : y; }
// 刚开始打复杂了,虽然理论上也能过
// 贡献即为逆序对个数
// 写丑了
int Calc(int f, int i, int j, int k, int F) {
int res = inf;
if(F == 1 && !j) return res;
if(F == 2 && !k) return res;
if(F == 0 && i - j - k == 0) return res;
for(int u = 0; u <= 2; u ++) {
if(u ^ F) {
if(F == 1) res = min(res, dp[f ^ 1][j - 1][k][u]);
if(F == 2) res = min(res, dp[f ^ 1][j][k - 1][u]);
if(F == 0) res = min(res, dp[f ^ 1][j][k][u]);
}
}
if(res == inf) return res;
if(F == 1) { // 想好了再打,把逻辑理清
res += max(0, k - pre[2][c[1][j]]); res += max(0, i - j - k - pre[0][c[1][j]]);
}
if(F == 2) {
res += max(0, j - pre[1][c[2][k]]); res += max(0, i - j - k - pre[0][c[2][k]]);
}
if(F == 0) {
res += max(0, j - pre[1][c[0][i - j - k]]); res += max(0, k - pre[2][c[0][i - j - k]]);
}
return res;
}
int main() {
freopen("s.in", "r", stdin);
freopen("s.out", "w", stdout);
scanf("%d%s", &n, s + 1);
for(int i = 1; i <= n; i ++) {
if(s[i] == 'R') a[i] = 0;
else if(s[i] == 'G') a[i] = 1;
else a[i] = 2;
pre[0][i] = pre[0][i - 1]; pre[1][i] = pre[1][i - 1]; pre[2][i] = pre[2][i - 1];
pre[a[i]][i] ++; g[a[i]] ++; c[a[i]][g[a[i]]] = i;
}
memset(dp, 0x3f, sizeof(dp)); dp[1][1][0][1] = 0; dp[1][0][1][2] = 0; dp[1][0][0][0] = 0;
for(int i = 2; i <= n; i ++) {
bool f = (i & 1);
for(int j = 0; j <= g[1]; j ++) {
for(int k = 0; k <= g[2]; k ++) {
if(i - j - k < 0 || i - j - k > g[0]) {
for(int u = 0; u <= 2; u ++) dp[f][j][k][u] = inf;
continue; // this is important
}
// printf("|%d %d|", i - j - k, g[0]);
for(int u = 0; u <= 2; u ++) dp[f][j][k][u] = Calc(f, i, j, k, u);//, printf("%d %d %d %d %d\n", i, j, k, u, dp[f][j][k][u]);
}
}
}
for(int i = 0; i <= g[1]; i ++) {
for(int j = 0; j <= g[2]; j ++) {
if(n - i - j < 0 || n - i - j > g[0]) continue;
res = Min(res, dp[n & 1][i][j][1]); res = Min(res, dp[n & 1][i][j][2]); res = Min(res, dp[n & 1][i][j][0]);
}
}
if(res == inf) res = -1;
printf("%d", res);
return 0;
}
Update:写丑了,其实根本不用考虑前一个的移动对他有什么影响。照样算最后答案除以 \(2\) 即可,妙啊!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号