可持久化1——主席树（可持久化线段树）
简介
主席树就是可持久化线段树，它的作用就是不停地访问某个历史版本，时间复杂度为O((n+m)logn)。
题目
洛谷3919（https://www.luogu.com.cn/problem/P3919）
如题，你需要维护这样的一个长度为 N 的数组，支持如下几种操作
-
在某个历史版本上修改某一个位置上的值
-
访问某个历史版本上的某一位置的值
此外，每进行一次操作（对于操作2，即为生成一个完全一样的版本，不作任何改动），就会生成一个新的版本。版本编号即为当前操作的编号（从1开始编号，版本0表示初始状态数组）
分析
先看看暴力做法：每次单点修改一个节点(数组模拟比线段树少一只log)，然后存入一个新的版本里。时间复杂度为O(nm),空间O(nm)。
这显然在洛谷你会看见一堆黑色（MLE+TLE）
这显然不可取，那我们有什么更好的做法吗？
主席树原理
我们观察，线段树的单点修改应该是这样的，比如我们要修改3号节点
我们发现，其实当我们进行线段树上单点修改时，只会修改红色路径上的点，而修改的点是log(n)个，也就是我们要新建log(n)个节点。
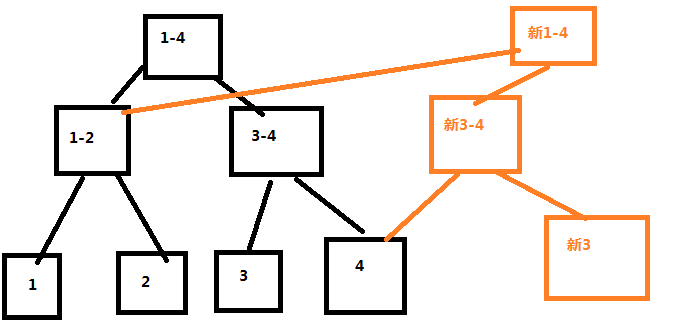
修改如上图：
主席树的一些特性：
1、主席树的根很多很多，且每个根都有一颗完整的线段树。
2、每一个节点的父亲都不止一个。
操作
接下来，一起收菜（It's show time）。
定义
我们要定义一个结构体，这个结构体需要存三个量，权值val，左儿子lson，右儿子rson。
为什么要存左右儿子？
因为我们这是主席树，要动态开点，已经不是线段树的左儿子为根*2，右儿子为根*2+1了。
struct tree{
int lson,rson,val;
}t[MAXN*20];
需要注意的是，这里的数组要开N的20倍大小。
建树
建树十分简单，和线段树基本一样。注意，这里用了动态开点。
void build(int &rot,int l,int r){//细心的你会发现这个rot是用了取址符的，意味着你只要改了rot，原来你弄进去的变量也会改
rot=++tot;//动态开店
if(l==r){
t[rot].val=n[l];
return;
}
int mid=l+r>>1;
build(t[rot].lson,l,mid);//这里可以直接写t[rot].lson，因为用了取址符
build(t[rot].rson,mid+1,r);
// t[rot].val=t[t[rot].lson].val+t[t[rot].rson].val;本题不用，本题不用求历史版本区间和
}
修改
修改操作时，我们先把当前节点copy一份，出来的就是上面图的橙色节点，连的都还是原来的左右儿子。
然后我们判断我们修改的节点是在左子树还是在右子树，然后不停地递归下去。
void clone(int &rot,int cl){
rot=++tot;
t[rot]=t[cl];
}
void update(int &rot,int l,int r,int cl,int loc,int value){//这里的rot依然用的是有取址符的
clone(rot,cl);//克隆一份
if(l==r){
t[rot].val=value;
return;
}
int mid=l+r>>1;
if(loc<=mid)update(t[rot].lson,l,mid,t[cl].lson,loc,value);//这里的t[rot].lson和t[cl].lson不要搞错
if(loc>mid)update(t[rot].rson,mid+1,r,t[cl].rson,loc,value);//同上
// t[rot].val=t[t[rot].lson].val+t[t[rot].rson].val;本题不用，本题不用求历史版本区间和
}
查询
查询就很容易了，简直就是线段树一样。
int Find(int rot,int l,int r,int loc){
if(l==r)return t[rot].val;
int mid=l+r>>1;
if(loc<=mid)return Find(t[rot].lson,l,mid,loc);
else return Find(t[rot].rson,mid+1,r,loc);
}
代码
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1000005;
int N,M,n[MAXN],tot,rt[MAXN],v,loc,c,value;
struct tree{
int lson,rson,val;
}t[MAXN*20];
void build(int &rot,int l,int r){
rot=++tot;
if(l==r){
t[rot].val=n[l];
return;
}
int mid=l+r>>1;
build(t[rot].lson,l,mid);
build(t[rot].rson,mid+1,r);
// t[rot].val=t[t[rot].lson].val+t[t[rot].rson].val;本题不用，本题不用求历史版本区间和
}
void clone(int &rot,int cl){
rot=++tot;
t[rot]=t[cl];
}
void update(int &rot,int l,int r,int cl,int loc,int value){
clone(rot,cl);
if(l==r){
t[rot].val=value;
return;
}
int mid=l+r>>1;
if(loc<=mid)update(t[rot].lson,l,mid,t[cl].lson,loc,value);
if(loc>mid)update(t[rot].rson,mid+1,r,t[cl].rson,loc,value);
// t[rot].val=t[t[rot].lson].val+t[t[rot].rson].val;本题不用，本题不用求历史版本区间和
}
int Find(int rot,int l,int r,int loc){
if(l==r)return t[rot].val;
int mid=l+r>>1;
if(loc<=mid)return Find(t[rot].lson,l,mid,loc);
else return Find(t[rot].rson,mid+1,r,loc);
}
int main(){
scanf("%d%d",&N,&M);
for(int i=1;i<=N;i++)
scanf("%d",&n[i]);
build(rt[0],1,N);
for(int i=1;i<=M;i++){
scanf("%d%d%d",&v,&c,&loc);
if(c==1){
scanf("%d",&value);
update(rt[i],1,N,rt[v],loc,value);
}
if(c==2){
printf("%d\n",Find(rt[v],1,N,loc));
rt[i]=rt[v];
}
}
return 0;
}
总结
主席树还是很容易的，只要你看的懂的话，这是本萌新第一次写博客，有什么建议可以在下面提，或私聊。
