树链剖分讲解及总结(重链剖分+长链剖分)
树链剖分是解决树上问题的一种常见数据结构，对于树上路径修改及路径信息查询等问题有着较优的复杂度。树链剖分分为两种：重链剖分和长链剖分，因为长链剖分不常见，应用也不广泛，所以通常说的树链剖分指的是重链剖分。在这里讲解并总结一下树链剖分的实现、优秀性质及应用。
重链剖分
先来介绍几个重链剖分的专业名词：
- 重儿子：每个点的子树中，子树大小(即节点数)最大的子节点
- 轻儿子：除重儿子外的其他子节点
- 重边：每个节点与其重儿子间的边
- 轻边：每个节点与其轻儿子间的边
- 重链：重边连成的链
- 轻链：轻边连成的链
重链剖分顾名思义是按轻重链进行剖分，对于每个点找到重儿子，如果多个子树节点数同样多，随便选一个作为重儿子就好了，一个点也可以看做一条重链。
用图来形象的描述一下，粗边就代表重边啦qwq
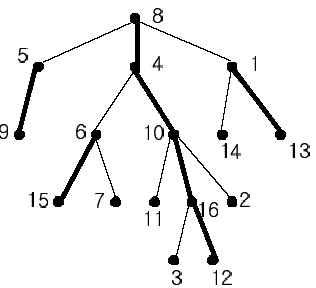
重链剖分的实现是由两次dfs来实现的，第一次dfs处理出每个点的重儿子son[]，子树大小size[]，深度d[]及父节点f[]
具体实现很简单，回溯时直接比较当前子节点和重儿子子树大小关系来更新重儿子
void dfs(int x)
{
size[x]=1;
d[x]=d[f[x]]+1;
for(int i=head[x];i;i=next[i])
{
if(to[i]!=f[x])
{
f[to[i]]=x;
dfs(to[i]);
size[x]+=size[to[i]];
if(size[to[i]]>size[son[x]])
{
son[x]=to[i];
}
}
}
}
而第二遍dfs则是要处理出每个点所在重链的链头top[]
void dfs2(int x,int tp)//dfs2(root,root);
{
top[x]=tp;
if(son[x])
{
dfs2(son[x],tp);
}
for(int i=head[x];i;i=next[i])
{
if(to[i]!=f[x]&&to[i]!=son[x])
{
dfs2(to[i],to[i]);
}
}
}
通过代码及图示可以发现重链剖分的一些性质：
1、所有重链互不相交，即每个点只属于一条重链
2、所有重链长度和等于节点数(链长指链上节点数)
3、一个点到根节点的路径上经过的边中轻边最多只有log条
前两个性质好理解，那么第三个性质是为什么呢？因为最坏情况就是这个点到根路径上经过的边都是轻边，那么每走一条轻边到达这个点的父节点就代表这个父节点至少还有一个与当前子树同样大的子树，也就是说每走一条轻边走到的点的子树大小就要*2，因此最多只能走log次。这也是为什么要选重儿子而不是随便一个儿子的原因。
重链剖分有什么用呢？
举个例子：求LCA
对于求x,y的lca，可以每次优先爬点所在重链链头深的点，如果两个点不在同一条重链上，那么直接把链头深的点跳到链头，重复这个过程，直到两个点处在同一条重链上，直接输出深度浅的点就是lca了。因为重链是直接跳到链头，时间复杂度是O(1)的，而跳轻边最多就log条，因此求两个点的lca时间复杂度是O(logn)。具体实现如下。
#include<set>
#include<map>
#include<stack>
#include<queue>
#include<cmath>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
int n,m,rt;
int x,y;
int head[500010];
int to[1000010];
int next[1000010];
int son[500010];
int size[500010];
int top[500010];
int d[500010];
int f[500010];
int tot;
void add(int x,int y)
{
tot++;
next[tot]=head[x];
head[x]=tot;
to[tot]=y;
}
void dfs(int x)
{
size[x]=1;
d[x]=d[f[x]]+1;
for(int i=head[x];i;i=next[i])
{
if(to[i]!=f[x])
{
f[to[i]]=x;
dfs(to[i]);
size[x]+=size[to[i]];
if(size[to[i]]>size[son[x]])
{
son[x]=to[i];
}
}
}
}
void dfs2(int x,int tp)
{
top[x]=tp;
if(son[x])
{
dfs2(son[x],tp);
}
for(int i=head[x];i;i=next[i])
{
if(to[i]!=f[x]&&to[i]!=son[x])
{
dfs2(to[i],to[i]);
}
}
}
int lca(int x,int y)
{
while(top[x]!=top[y])
{
if(d[top[x]]<d[top[y]])
{
swap(x,y);
}
x=f[top[x]];
}
return d[x]<d[y]?x:y;
}
int main()
{
scanf("%d%d%d",&n,&m,&rt);
for(int i=1;i<n;i++)
{
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
dfs(rt);
dfs2(rt,rt);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&x,&y);
printf("%d\n",lca(x,y));
}
}
通过用树链剖分求lca我们发现重链剖分重链的用途——O(1)移动到链头！但只是能求lca了，和刚开始写的维护树上信息也没关系啊?
通过第二次dfs可以观察到，每个点遍历子节点时优先遍历的是重儿子，这说明什么？每条重链的dfs序上的位置是连续的一段，而每一次在树上移动是直接移动到链头，这就可以对这一条重链上的信息区间修改或者查询，直接把dfs序架在线段树上就能实现了！事实上按优先遍历重儿子得出的dfs序就是树剖序。
这样对于文章开头提到的维护路径信息就可以对树剖序建线段树通过爬lca时每次跳链头来区间修改或查询。因为单次修改或查询线段树时间复杂度是O(logn)，所以单次对路径修改或查询时间复杂度就是O(log2n）。
树链剖分+线段树的题比较多，在这里只推荐几个经典题目
长链剖分
长链剖分和重链剖分差不多，只不过是将子树中深度最大的子节点当成重儿子，而维护的信息也从size[]变成了mx[]表示子树中的最大深度。
为了方便讲解，节点与重儿子之间的边就叫长边吧，其他边叫短边。
长链剖分也同样需要两遍dfs来维护信息，与重链剖分类似，在这里不再放代码，两遍dfs在下面lca的代码中可以看到。
在某些特殊情况中长链剖分和重链剖分可能相同。
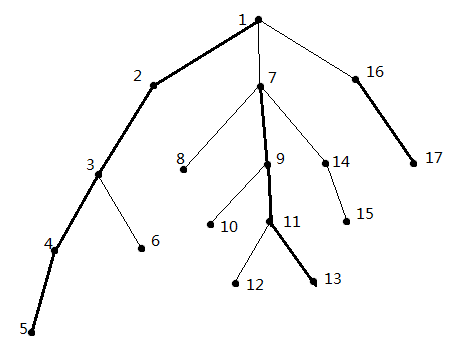
长链剖分有一些更好的性质：
1、任意点的任意祖先所在长链长度一定大于等于这个点所在长链长度
2、所有长链长度之和就是总节点数
3、一个点到根的路径上经过的短边最多有√n条
同样证明一下第三个性质，因为一个点x往上走一条短边就意味着它走到的点至少还有一个长度和x往下最长链长度相同的链。这样每走一条短边要加的点数为1、2、3、4……所以要加的点数是k2个(k是走的短边数,严格来说应该是k*(k+1)/2)，因此k最大为√n。这样也就说明了用长链剖分求lca的时间复杂度是O(n√n)。
长链剖分求lca的过程和重链剖分一样，在这里就不再说了。
#include<set>
#include<map>
#include<stack>
#include<queue>
#include<cmath>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
int n,m,rt;
int x,y;
int head[500010];
int to[1000010];
int next[1000010];
int son[500010];
int mx[500010];
int top[500010];
int d[500010];
int f[500010];
int tot;
void add(int x,int y)
{
tot++;
next[tot]=head[x];
head[x]=tot;
to[tot]=y;
}
void dfs(int x)
{
d[x]=d[f[x]]+1;
mx[x]=d[x];
for(int i=head[x];i;i=next[i])
{
if(to[i]!=f[x])
{
f[to[i]]=x;
dfs(to[i]);
mx[x]=max(mx[to[i]],mx[x]);
if(mx[to[i]]>mx[son[x]])
{
son[x]=to[i];
}
}
}
}
void dfs2(int x,int tp)
{
top[x]=tp;
if(son[x])
{
dfs2(son[x],tp);
}
for(int i=head[x];i;i=next[i])
{
if(to[i]!=f[x]&&to[i]!=son[x])
{
dfs2(to[i],to[i]);
}
}
}
int lca(int x,int y)
{
while(top[x]!=top[y])
{
if(d[top[x]]<d[top[y]])
{
swap(x,y);
}
x=f[top[x]];
}
return d[x]<d[y]?x:y;
}
int main()
{
scanf("%d%d%d",&n,&m,&rt);
for(int i=1;i<n;i++)
{
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
dfs(rt);
dfs2(rt,rt);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&x,&y);
printf("%d\n",lca(x,y));
}
}
长链剖分性质的应用有一道练习题BZOJ3252攻略
长链剖分应用：
O(nlogn)预处理，单次O(1)在线查询一个点的k级祖先
这个应用不是很广，因为只有在n特别大时才能体现出优势，但对于某些题可以简便地找到k级祖先。
首先想最暴力的方法每次朴素爬到父亲节点，这样单次查询时间复杂度是O(n)。
再进行优化，用倍增往上爬，单次时间复杂度O(logn)
因为倍增是满log的，那么用另一种求lca的方法重链剖分，这样虽然还是O(logn)，但常数小了一点
再想想能不能把倍增和重链剖分一起用？先找出比k小的最高的2的幂次，然后维护每个点的往上跳的倍增数组，先跳2的最高次幂再重链剖分，这样快了一点，但还是不能O(1)。
那么我们能不能把跳完2的最高次幂的那个点的祖先都记录下来呢？这样预处理时间复杂度就爆炸了。
如果只预处理每条重链链头的祖先和链上的节点呢？但往上要预处理多长的祖先？
这时联想上面讲到的长链剖分的第一个性质，将重链剖分换成长链剖分，暴力预处理每个链头往上链长个祖先及这条链上的所有点，因为只有链头预处理，而所有链长和是节点总数，所以预处理这一步时间复杂度是O(2n)。再预处理出所有数二进制的最高次幂，每次跳最大一步之后O(1)查询。
具体怎么查？为什么往上预处理链长个祖先？
我们分类讨论：
1、当k级祖先在当前链上时，直接查链头存的链信息
2、当k级祖先不在当前链上但在跳2的最高次幂到的点x所在的链上时，直接查点x所在那条链的链头存的链信息
3、当k及祖先既不在当前链上，也不在跳2的最高次幂到的点x所在的链上时，因为x距离查询点深度最少为k/2(跳的是2的最高次幂)，那么x往下的长链长度至少为k/2，也就是说x所在长链长度至少为k/2，x所在链的链头往上预处理的祖先至少有k/2个，一定包含k级祖先。
这就是为什么要用长链剖分而不是重链剖分的原因，重链剖分没有长链剖分的第一个性质。
#include<queue>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
int n,m;
int x,y;
int tot;
int ans;
int head[300300];
int nex[600600];
int to[600600];
int f[300300][20];
int son[300300];
int mx[300300];
int d[300300];
int top[300300];
int st[600600];
vector<int>s[300300];
vector<int>t[300300];
void add(int x,int y)
{
tot++;
nex[tot]=head[x];
head[x]=tot;
to[tot]=y;
}
void dfs(int x,int fa)
{
d[x]=d[fa]+1;
mx[x]=d[x];
f[x][0]=fa;
for(int i=1;i<=19;i++)
{
if(f[x][i-1])
{
f[x][i]=f[f[x][i-1]][i-1];
}
else
{
break;
}
}
for(int i=head[x];i;i=nex[i])
{
if(to[i]!=fa)
{
dfs(to[i],x);
if(mx[to[i]]>mx[son[x]])
{
son[x]=to[i];
mx[x]=mx[to[i]];
}
}
}
}
void dfs2(int x,int tp)
{
top[x]=tp;
if(son[x])
{
dfs2(son[x],tp);
}
for(int i=head[x];i;i=nex[i])
{
if(to[i]!=f[x][0]&&to[i]!=son[x])
{
dfs2(to[i],to[i]);
}
}
}
void find(int x)
{
int rt=x;
int len=mx[x]-d[x];
x=f[rt][0];
while(d[rt]-d[x]<=len&&x)
{
s[rt].push_back(x);
x=f[x][0];
}
x=rt;
while(son[x])
{
t[rt].push_back(son[x]);
x=son[x];
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<n;i++)
{
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
dfs(1,0);
dfs2(1,1);
st[1]=0;
for(int i=2;i<=n;i++)
{
st[i]=st[i>>1]+1;
}
for(int i=1;i<=n;i++)
{
if(i==top[i])
{
find(i);
}
}
scanf("%d",&m);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&x,&y);
x=x^ans;
y=y^ans;
if(y==0)
{
ans=x;
}
else if(y>=d[x])
{
ans=0;
}
else
{
x=f[x][st[y]];
y-=(1<<st[y]);
if(y==0)
{
ans=x;
}
else if(y<d[x]-d[top[x]])
{
ans=t[top[x]][d[x]-d[top[x]]-y-1];
}
else if(y==d[x]-d[top[x]])
{
ans=top[x];
}
else
{
ans=s[top[x]][y-d[x]+d[top[x]]-1];
}
}
printf("%d\n",ans);
}
}
练习题只找到一道BZOJ4381
O(n)处理可合并的与深度有关的子树信息(例如某深度点数、某深度点权和)
首先还是先想暴力，dfs整棵树，回溯时将每一深度的信息合并，时间复杂度O(n*maxdep)
再优化一下，还是想到重链剖分，因为每个点合并时第一个子节点可以直接继承下来(继承一般是用指针O(1)优化，具体后面再讲)，剩下子树暴力遍历，因为重链剖分后每个点不被继承而被暴力遍历最多logn次(每个点到根路径上最多log条轻边是需要被遍历的)，因此时间复杂度是O(nlogn)。
再想想能发现根本不用遍历其他子树，只要合并子树已有信息就好了。
但我们发现重链剖分在合并深度信息时不怎么优秀，因为每个点的轻儿子可能深度更深，合并还是很慢。
重链剖分不具有重儿子最深的性质但长链剖分具有啊！因此只要把重链剖分换成长链剖分，每次还是继承重儿子，其他的暴力合并。那么这样的时间复杂度呢？我们考虑一棵子树信息被暴力合并当且仅当这棵子树的根节点与其父节点之间的边是短边，合并的代价是这棵子树中最长链的长度(也就是这棵子树的深度)，而这棵子树的根节点就是这个最长链的链头，那么也就转化成了只有每条链的链头会被暴力合并且合并的时间复杂度是链长。因为所有链长和是n，所以这样做的时间复杂度就是O(n)。有了这个应用就可以优化许多与深度有关的树形DP了。
例如BZOJ4543
再来说一下怎么用指针O(1)优化。
因为继承重儿子相当于把重儿子的数组复制一遍，那么我们可以把所有节点的数组开成一个大数组，而每个节点的数组变成指针数组，每次继承时O(1)把父节点指针移到重儿子数组指针处，因为继承之后重儿子信息就没用了，因此暴力合并可以直接在父节点指针指向的数组那一段直接修改。
当然也不是所有情况都用指针来优化，如果求某一深度区间的信息时，可以求出长链剖分序，每次将轻儿子信息合并到长链上，之后查询每个点时只要查询这个点往下的长链上的信息就是整棵子树中的信息了。
例如BZOJ1758
