可持久化线段树(主席树)讲解
线段树是一种非常实用的数据结构，可以将区间上一些满足结合律的信息(比如最大最小值，区间和，区间异或和)统计起来，便于查询。线段树也就是将分块的思想用树形结构来体现。而今天要讲的不是普通的线段树而是将线段树可持久化。
在讲可持久化线段树之前先说一种别样的线段树——权值线段树。我们知道一般的线段树每个叶子节点代表的是在原序列中对应下标的那个数，存储的也是那个数的大小，而每个非叶子节点维护的区间也是原序列中对应区间的信息。但权值线段树中每个叶子节点代表的是权值，存储的也是权值为它的数的信息，而每个非叶子节点则维护的是权值在[l,r]中的所有数的信息。举个例子，如下图所示。
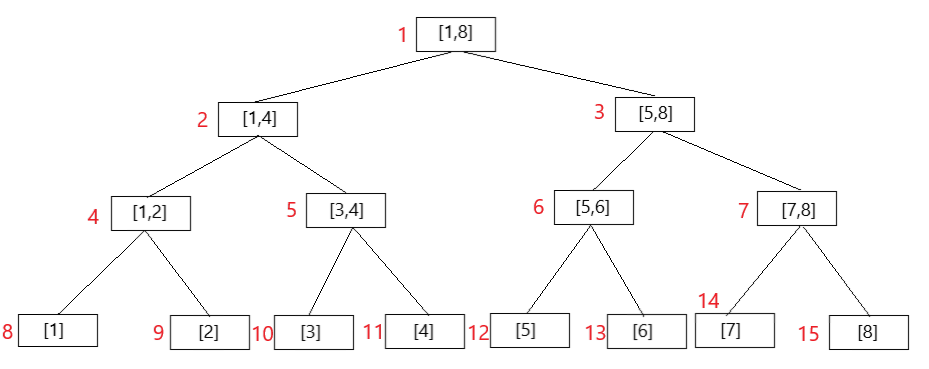
如果是普通线段树，9节点代表原序列中第二个数，4节点维护的是原序列前两个数的信息。但如果这是权值线段树，9节点就代表权值为2的数，而4节点则维护的是所有权值为[1,2]的数的信息。
权值线段树代表的可以是真实的权值，也可以是离散后的数的大小排名。权值线段树因为每个点都代表着权值因此可以很容易的查询第k大的数或者权值小于等于k的数有多少个这种和权值相关的问题。
下面该步入讲解正题——可持久化线段树
首先要知道什么是可持久化？就是保留历史版本，例如让你往权值线段树中依次插入一列数，在你插入完所有数之后询问在你插入第x个数之后所有数中第k大的是多少？这就需要你记录每个时刻的线段树，最暴力也是最容易想到的方法是每次插入一个数之前再建一棵线段树复制上一时刻的线段树，然后再在新建的树上插入。但这样不仅占很大空间还很费时间。结合线段树单点修改的操作不难发现每次插入或修改只会改变logn个节点，其他点并没有什么变动，因此我们只要每次把修改的logn个节点建出来，没修改的那部分点就沿用上一时刻的点就好了。什么意思呢？还是拿图来说话吧。(因为美观原因，有的点的左右子树反过来了)
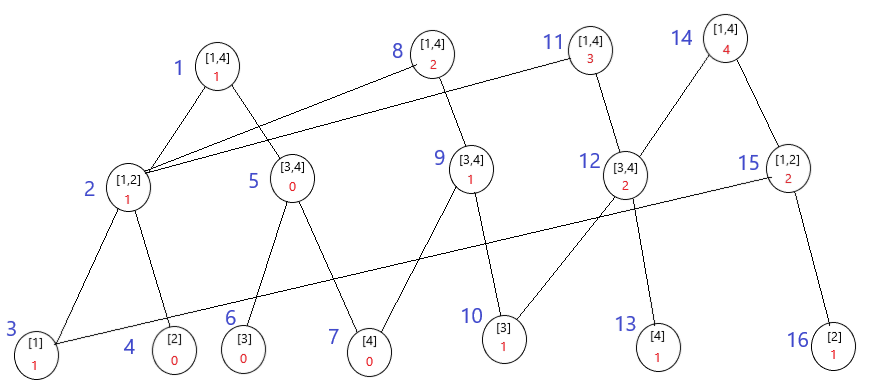
例如依次插入1,3,4,2，这四个时刻的根节点分别为1,8,11,14。当插入3时，发现它的左子树并没有改变，于是直接连到上一个时刻的根节点对应的左子树，发现右子树需要继续遍历，建出9节点，重复上述操作，直到建完一条链。这样当查询某一时刻时只要从那一时刻的根节点开始往下查询即可。
通常遇到的题所用到的都是非完全可持久化线段树，也就是只能保留历史版本的线段树，即使修改历史版本也是在新版本上根据历史版本进行修改。而完全可持久化线段树是指可以在历史版本上修改的可持久化线段树，即在某一历史版本上修改会影响之后版本。这就需要其他一些数据结构辅助修改操作，一般用树状数组来实现。怎么实现呢？一般有两种：第一种是树状数组套主席树，也就是在树状数组的每个节点上建一棵主席树，这种内存较大；第二种是树状数组套权值线段树，也可以看做是以树状数组状态来转移的主席树。我们知道树状数组维护的是一个前缀和，而可持久化线段树也相当于维护的是一个前缀和，所以每次修改和查询也可以像树状数组一样跳lowbit。以一个序列建可持久化线段树为例，加入一个点就以当前点下标开始每次往上跳lowbit，在对应时刻的线段树中加入这个数，修改就是先删除再添加。求一个时刻的版本就是往下跳lowbit，每个点加上每次lowbit跳到的时刻线段树中对应的点的信息。
最后说一下主席树和可持久化线段树的区别，主席树特指可持久化权值线段树，它属于一种可持久化线段树。
可持久化线段树一般有三种建树方法：
1、对序列建树，常见方法，每个点一个时刻的树。
2、树上主席树，树上每个点一棵线段树，每个点的线段树从父节点修改而来。
3、对深度建立主席树，每个深度建立一棵主席树，将该深度的所有点都加进来，当树上问题对深度有限制时用这个。
这里有几个小东西需要注意：
1、每棵线段树不一定是由上一时刻转移来的，要因题而异。
2、可持久化线段树不需要刚开始建出整棵树，只要建出需要的点的那条链就够了，之后每次修改也只建一条链(也就是动态开点)。
3、可持久化线段树的优势在于它可以强制在线。
附上两个模板：
1、可持久化数组(单点修改，单点查询)luoguP3919
#include<map>
#include<set>
#include<queue>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define mid (L+R)/2
using namespace std;
int n,m;
int cnt;
int num;
int x,y,z,k;
int l[30000010];
int r[30000010];
int s[30000010];
int root[1000010];
int build(int L,int R)
{
int rt=++cnt;
if(L==R)
{
scanf("%d",&x);
s[rt]=x;
}
else
{
l[rt]=build(L,mid);
r[rt]=build(mid+1,R);
}
return rt;
}
int updata(int pre,int L,int R,int k,int v)
{
int rt=++cnt;
l[rt]=l[pre];
r[rt]=r[pre];
if(L==R)
{
s[rt]=v;
}
else
{
if(k<=mid)
{
l[rt]=updata(l[pre],L,mid,k,v);
}
else
{
r[rt]=updata(r[pre],mid+1,R,k,v);
}
}
return rt;
}
int copy(int pre,int L,int R)
{
int rt=++cnt;
l[rt]=l[pre];
r[rt]=r[pre];
return rt;
}
int query(int L,int R,int rt,int v)
{
if(L==R)
{
return s[rt];
}
else
{
if(v<=mid)
{
return query(L,mid,l[rt],v);
}
else
{
return query(mid+1,R,r[rt],v);
}
}
}
int main()
{
scanf("%d%d",&n,&m);
root[0]=build(1,n);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&x,&k);
if(k==1)
{
scanf("%d%d",&y,&z);
root[++num]=updata(root[x],1,n,y,z);
}
else
{
scanf("%d",&y);
printf("%d\n",query(1,n,root[x],y));
root[++num]=copy(root[x],1,n);
}
}
}
2、可持久化线段树(求区间第k大)luoguP3834
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<ctime>
#include<iostream>
#include<cmath>
#define mid (L+R)/2
using namespace std;
int cnt;
int n,q,m;
int a[200010];
int b[200010];
int l[200010<<5];
int r[200010<<5];
int sum[200010<<5];
int root[200010];
int build(int L,int R)
{
int rt=++cnt;
sum[rt]=0;
if(L<R)
{
l[rt]=build(L,mid);
r[rt]=build(mid+1,R);
}
return rt;
}
int updata(int pre,int L,int R,int x)
{
int rt=++cnt;
l[rt]=l[pre];
r[rt]=r[pre];
sum[rt]=sum[pre]+1;
if(L<R)
{
if(x<=mid)
{
l[rt]=updata(l[pre],L,mid,x);
}
else
{
r[rt]=updata(r[pre],mid+1,R,x);
}
}
return rt;
}
int query(int ll,int rr,int L,int R,int k)
{
if(L>=R)
{
return L;
}
int x=sum[l[rr]]-sum[l[ll]];
if(x>=k)
{
return query(l[ll],l[rr],L,mid,k);
}
else
{
return query(r[ll],r[rr],mid+1,R,k-x);
}
}
int main()
{
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
b[i]=a[i];
}
sort(b+1,b+1+n);
m=unique(b+1,b+1+n)-b-1;
root[0]=build(1,m);
for(int i=1;i<=n;i++)
{
int t=lower_bound(b+1,b+1+m,a[i])-b;
root[i]=updata(root[i-1],1,m,t);
}
while(q--)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
int t=query(root[x-1],root[y],1,m,z);
printf("%d\n",b[t]);
}
}
推荐几道经典练习题：
