[NOIP]2017列队——旋转treap/非旋转treap
Sylvia 是一个热爱学习的女孩子。
前段时间,Sylvia 参加了学校的军训。众所周知,军训的时候需要站方阵。 Sylvia所在的方阵中有n × m名学生,方阵的行数为 n,列数为m。
为了便于管理,教官在训练开始时,按照从前到后,从左到右的顺序给方阵中的学生从 1 到 n × m 编上了号码(参见后面的样例)。即:初始时,第 i 行第 j 列的学生的编号是(i − 1) × m + j。
然而在练习方阵的时候,经常会有学生因为各种各样的事情需要离队。在一天中,一共发生了 q 件这样的离队事件。每一次离队事件可以用数对(x, y) (1≤x≤n, 1≤y≤m)描述,表示第 x 行第 y 列的学生离队。
在有学生离队后,队伍中出现了一个空位。为了队伍的整齐,教官会依次下达这样的两条指令:
1. 向左看齐。这时第一列保持不动,所有学生向左填补空缺。不难发现在这条指令之后,空位在第 x 行第 m 列。
2. 向前看齐。这时第一行保持不动,所有学生向前填补空缺。不难发现在这条指令之后,空位在第 n 行第 m 列。
教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后,下一个学生才能离队。因此在每一个离队的学生要归队时,队伍中有且仅有第 n 行第 m 列一个空位,这时这个学生会自然地填补到这个位置。
因为站方阵真的很无聊,所以 Sylvia 想要计算每一次离队事件中,离队的同学的编号是多少。
注意:每一个同学的编号不会随着离队事件的发生而改变,在发生离队事件后方阵中同学的编号可能是乱序的。
输入共 q+1 行。
第1 行包含 3 个用空格分隔的正整数 n, m, q,表示方阵大小是 n行 m 列,一共发生了q 次事件。
接下来 q 行按照事件发生顺序描述了 q 件事件。每一行是两个整数 x, y,用一个空格分隔,表示这个离队事件中离队的学生当时排在第 x 行第 y 列。
按照事件输入的顺序,每一个事件输出一行一个整数,表示这个离队事件中离队学生的编号。
样例输入
样例输出
1 1 4
【样例解释】
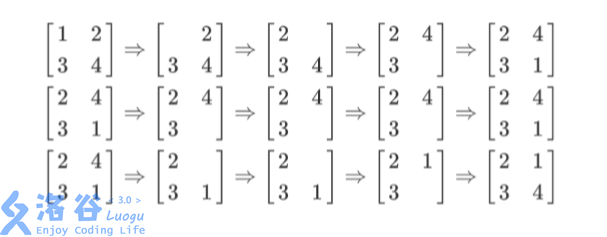
列队的过程如上图所示,每一行描述了一个事件。
在第一个事件中,编号为 1 的同学离队,这时空位在第一行第一列。接着所有同学向左标齐,这时编号为 2 的同学向左移动一步,空位移动到第一行第二列。然后所有同学向上标齐,这时编号为 4 的同学向上一步,这时空位移动到第二行第二列。最后编号为1 的同学返回填补到空位中。
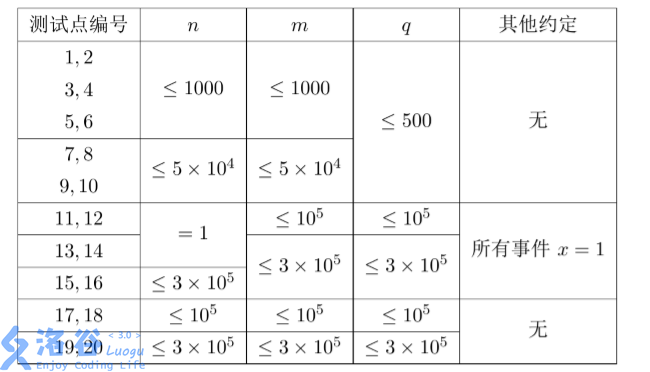
【数据规模】
数据保证每一个事件满足 1≤x≤n,1≤y≤m。
这道题有许多做法,树状数组、线段树、平衡树都能做。这里只讲一下平衡树treap的做法。
通过题意我们会发现每次操作只改变第x行和最后一列。所以我们可以建n+1个平衡树(每行前m-1个数是一个,最后一列是一个),这样就可以快速查找并删除要操作的点并在最后一列插入删除的点。时间复杂度是O(Q*logN)级别,但看一下数据范围n*m的矩阵9*1010(比全世界人口都要多qwq),显然是存不下的。但只有3*105次查询,所以有许多点是不会被改动的,那么我们可以把这些点缩成一个点,然后记录一下每个点的左端和长度。每次操作时把操作的数所在点分成三个点(l~x-1;x;x+1~r)。所以最多只有2*q+2*n个点。每个平衡树在初始时只有一个点(最后一列的那个树是n个点)。注意非旋转treap分裂时并不是像常规一样分裂成两棵树,而是分裂成两个数和查询点三部分。
旋转treap
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int a,b;
int tot;
int n,m,q;
long long ans;
int w[3000010];
int ls[3000010];
int rs[3000010];
int root[300010];
int size[3000010];
long long l[3000010];
long long r[3000010];
void updata(int x)
{
size[x]=size[ls[x]]+size[rs[x]]+r[x]-l[x]+1;
}
void lturn(int &x)
{
if(!rs[x])
{
return ;
}
int t=rs[x];
rs[x]=ls[t];
ls[t]=x;
size[t]=size[x];
updata(x);
x=t;
}
void rturn(int &x)
{
if(!ls[x])
{
return ;
}
int t=ls[x];
ls[x]=rs[t];
rs[t]=x;
size[t]=size[x];
updata(x);
x=t;
}
void rotate(int &x)
{
if(w[rs[x]]<w[x])
{
lturn(x);
}
if(w[ls[x]]<w[x])
{
rturn(x);
}
}
void insert(int &x,long long L,long long R)
{
if(!x)
{
x=++tot;
l[x]=L;
r[x]=R;
w[x]=rand();
updata(x);
return ;
}
insert(rs[x],L,R);
updata(x);
rotate(x);
}
void del(int &x,int num)
{
if(!x)
{
return ;
}
if(x==num)
{
if(ls[x]*rs[x]==0)
{
x=ls[x]+rs[x];
}
else if(w[ls[x]]<w[rs[x]])
{
rturn(x);
}
else if(w[ls[x]]>=w[rs[x]])
{
lturn(x);
}
del(x,num);
return ;
}
if(ls[x]==num)
{
del(ls[x],num);
}
if(rs[x]==num)
{
del(rs[x],num);
}
updata(x);
}
void find1(int &x,int v)
{
if(!x)
{
return ;
}
if(size[ls[x]]>=v)
{
find1(ls[x],v);
updata(x);
rotate(x);
return ;
}
else if(size[x]-size[rs[x]]<v)
{
find1(rs[x],v-size[x]+size[rs[x]]);
updata(x);
rotate(x);
return ;
}
v-=size[ls[x]];
ans=l[x]+v-1;
if(v==1&&v==size[x]-size[rs[x]]-size[ls[x]])
{
del(x,x);
return ;
}
if(v==1)
{
l[x]++;
updata(x);
}
else if(v==size[x]-size[ls[x]]-size[rs[x]])
{
r[x]--;
updata(x);
}
else
{
int sum=++tot;
r[sum]=r[x];
r[x]=l[x]+v-2;
l[sum]=l[x]+v;
rs[sum]=rs[x];
rs[x]=sum;
updata(sum);
updata(x);
w[sum]=rand();
rotate(x);
}
}
void find2(int &x,int v)
{
if(!x)
{
return ;
}
if(size[ls[x]]>=v)
{
find2(ls[x],v);
updata(x);
rotate(x);
return ;
}
else if(size[x]-size[rs[x]]<v)
{
find2(rs[x],v-size[x]+size[rs[x]]);
updata(x);
rotate(x);
return ;
}
ans=l[x];
del(x,x);
}
int main()
{
srand(37975);
scanf("%d%d%d",&n,&m,&q);
for(long long i=1;i<=n;i++)
{
insert(root[i],(i-1)*m+1,(i-1)*m+m-1);
}
for(long long i=1;i<=n;i++)
{
insert(root[n+1],i*m,i*m);
}
while(q--)
{
scanf("%d%d",&a,&b);
if(b<m)
{
find1(root[a],b);
}
else
{
find2(root[n+1],a);
}
long long s=ans;
printf("%lld\n",s);
if(b<m)
{
find2(root[n+1],a);
long long t=ans;
insert(root[a],t,t);
}
insert(root[n+1],s,s);
}
return 0;
}
非旋转treap
#include<set>
#include<map>
#include<queue>
#include<stack>
#include<cmath>
#include<cstdio>
#include<vector>
#include<bitset>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
#define pr pair<int,ll>
using namespace std;
int rs[2000010];
int ls[2000010];
ll l[2000010];
ll r[2000010];
int size[2000010];
int num[2000010];
int root[500010];
int v[2000010];
int n,m,q;
int x,y;
int cnt;
int a,b,c,d;
pr now;
int build(ll L,ll R)
{
int rt=++cnt;
size[rt]=num[rt]=(int)(R-L+1);
l[rt]=L;
r[rt]=R;
v[rt]=rand();
return rt;
}
void pushup(int rt)
{
size[rt]=size[ls[rt]]+size[rs[rt]]+num[rt];
}
pr split(int rt,int k,int &x,int &y)
{
if(size[ls[rt]]>=k)
{
y=rt;
pr res=split(ls[rt],k,x,ls[y]);
pushup(rt);
return res;
}
else if(size[ls[rt]]+num[rt]>=k)
{
x=ls[rt];
y=rs[rt];
return make_pair(rt,1ll*(k-size[ls[rt]]+l[rt]-1));
}
else
{
x=rt;
pr res=split(rs[rt],k-size[ls[rt]]-num[rt],rs[x],y);
pushup(rt);
return res;
}
}
int merge(int x,int y)
{
if(!x||!y)
{
return x+y;
}
if(v[x]<v[y])
{
rs[x]=merge(rs[x],y);
pushup(x);
return x;
}
else
{
ls[y]=merge(x,ls[y]);
pushup(y);
return y;
}
}
int main()
{
srand(12378);
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=n;i++)
{
root[i]=build(1ll*(i-1)*m+1,1ll*i*m-1);
}
root[n+1]=build(1ll*m,1ll*m);
for(int i=2;i<=n;i++)
{
root[n+1]=merge(root[n+1],build(1ll*i*m,1ll*i*m));
}
while(q--)
{
scanf("%d%d",&x,&y);
if(y==m)
{
now=split(root[n+1],x,a,b);
ls[now.first]=rs[now.first]=0;
size[now.first]=num[now.first];
printf("%lld\n",now.second);
root[n+1]=merge(a,merge(b,now.first));
}
else
{
now=split(root[x],y,a,b);
printf("%lld\n",now.second);
if(l[now.first]!=now.second)
{
cnt++;
l[cnt]=l[now.first];
r[cnt]=now.second-1;
size[cnt]=num[cnt]=(int)(r[cnt]-l[cnt]+1);
v[cnt]=rand();
a=merge(a,cnt);
}
if(r[now.first]!=now.second)
{
cnt++;
l[cnt]=now.second+1;
r[cnt]=r[now.first];
size[cnt]=num[cnt]=(int)(r[cnt]-l[cnt]+1);
v[cnt]=rand();
b=merge(cnt,b);
}
root[x]=merge(a,b);
l[now.first]=now.second;
r[now.first]=now.second;
num[now.first]=size[now.first]=1;
ls[now.first]=rs[now.first]=0;
root[n+1]=merge(root[n+1],now.first);
now=split(root[n+1],x,c,d);
ls[now.first]=rs[now.first]=0;
size[now.first]=num[now.first];
root[n+1]=merge(c,d);
root[x]=merge(root[x],now.first);
}
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号