BZOJ3224普通平衡树——旋转treap
题目:
此为平衡树系列第一道:普通平衡树您需要写一种数据结构,来维护一些数,其中需要提供以下操作:
1. 插入x数
2. 删除x数(若有多个相同的数,因只删除一个)
3. 查询x数的排名(若有多个相同的数,因输出最小的排名)
4. 查询排名为x的数
5. 求x的前驱(前驱定义为小于x,且最大的数)
6. 求x的后继(后继定义为大于x,且最小的数)
n<=100000 所有数字均在-107到107内。
10 1 106465 4 1 1 317721 1 460929 1 644985 1 84185 1 89851 6 81968 1 492737 5 493598
106465 84185 492737
变量声明:size[x],以x为根节点的子树大小;ls[x],x的左儿子;rs[x],x的右子树;r[x],x节点的随机数;v[x],x节点的权值;w[x],x节点所对应的权值的数的个数。
root,树的总根;tot,树的大小。
treap是tree(树)和heap(堆)的组合词,顾名思义就是在树上建堆,所以treap满足堆的性质,但treap又是一个平衡树所以也满足平衡树的性质(对于每个点,它的左子树上所有点都比它小,它的右子树上所有点都比他大,故平衡树的中序遍历就是树上所有点点权的顺序数列)。
先介绍几个基本旋转treap操作:
1.左旋和右旋
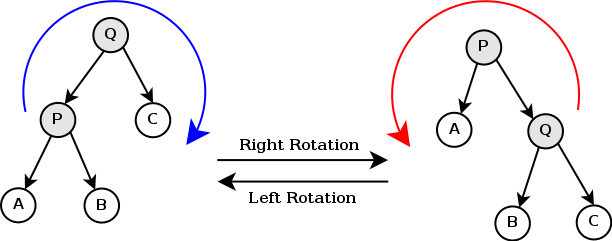
左旋即把Q旋到P的父节点,右旋即把P旋到Q的父节点。
以右旋为例:因为Q>B>P所以在旋转之后还要满足平衡树性质所以B要变成Q的左子树。在整个右旋过程中只改变了B的父节点,P的右节点和父节点,Q的左节点的父节点,与A,B,C的子树无关。
void rturn(int &x)
{
int t;
t=ls[x];
ls[x]=rs[t];
rs[t]=x;
size[t]=size[x];
up(x);
x=t;
}
void lturn(int &x)
{
int t;
t=rs[x];
rs[x]=ls[t];
ls[t]=x;
size[t]=size[x];
up(x);
x=t;
}
2.查询
我们以查询权值为x的点为例,从根节点开始走,判断x与根节点权值大小,如果x大就向右下查询,比较x和根右儿子大小;如果x小就向左下查询,直到查询到等于x的节点或查询到树的最底层。
3.插入
插入操作就是遵循平衡树性质插入到树中。对于要插入的点x和当前查找到的点p,判断x与p的大小关系。注意在每次向下查找时因为要保证堆的性质,所以要进行左旋或右旋。
void insert_sum(int x,int &i)
{
if(!i)
{
i=++tot;
w[i]=size[i]=1;
v[i]=x;
r[i]=rand();
return ;
}
size[i]++;
if(x==v[i])
{
w[i]++;
}
else if(x>v[i])
{
insert_sum(x,rs[i]);
if(r[rs[i]]<r[i])
{
lturn(i);
}
}
else
{
insert_sum(x,ls[i]);
if(r[ls[i]]<r[i])
{
rturn(i);
}
}
return ;
}
4.上传
每次旋转后因为子树有变化所以要修改父节点的子树大小。
void up(int x)
{
size[x]=size[rs[x]]+size[ls[x]]+w[x];
}
5.删除
删除节点的方法和堆类似,要把点旋到最下层再删,如果一个节点w不是1那就把w--就行。
void delete_sum(int x,int &i)
{
if(i==0)
{
return ;
}
if(v[i]==x)
{
if(w[i]>1)
{
w[i]--;
size[i]--;
return ;
}
if((ls[i]*rs[i])==0)
{
i=ls[i]+rs[i];
}
else if(r[ls[i]]<r[rs[i]])
{
rturn(i);
delete_sum(x,i);
}
else
{
lturn(i);
delete_sum(x,i);
}
return ;
}
size[i]--;
if(v[i]<x)
{
delete_sum(x,rs[i]);
}
else
{
delete_sum(x,ls[i]);
}
return ;
}
6.查找排名
查找操作和上面说的差不多,只不过要注意当查找一个节点右子树时要把答案加上这个点的w和这个节点左子树的size。
int ask_num(int x,int i)
{
if(i==0)
{
return 0;
}
if(v[i]==x)
{
return size[ls[i]]+1;
}
if(v[i]<x)
{
return ask_num(x,rs[i])+size[ls[i]]+w[i];
}
return ask_num(x,ls[i]);
}
7.查找权值
和查找排名差不多,查找右子树时要将所查找排名减掉父节点w和父节点的左子树的size。
int ask_sum(int x,int i)
{
if(i==0)
{
return 0;
}
if(x>size[ls[i]]+w[i])
{
return ask_sum(x-size[ls[i]]-w[i],rs[i]);
}
else if(size[ls[i]]>=x)
{
return ask_sum(x,ls[i]);
}
else
{
return v[i];
}
}
8.查找前驱/后继
直接判断大小查询就好了qwq
前驱
void ask_front(int x,int i)
{
if(i==0)
{
return ;
}
if(v[i]<x)
{
answer=i;
ask_front(x,rs[i]);
return ;
}
else
{
ask_front(x,ls[i]);
return ;
}
return ;
}
后继
void ask_back(int x,int i)
{
if(i==0)
{
return ;
}
if(v[i]>x)
{
answer=i;
ask_back(x,ls[i]);
return ;
}
else
{
ask_back(x,rs[i]);
return ;
}
}
最后附上完整代码(虽然有点长但自认为很好理解也很详细。。。)
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<iostream>
#include<ctime>
using namespace std;
int n;
int opt;
int x;
int size[100001];
int rs[100001];
int ls[100001];
int v[100001];
int w[100001];
int r[100001];
int tot;
int root;
int answer;
void up(int x)
{
size[x]=size[rs[x]]+size[ls[x]]+w[x];
}
void rturn(int &x)
{
int t;
t=ls[x];
ls[x]=rs[t];
rs[t]=x;
size[t]=size[x];
up(x);
x=t;
}
void lturn(int &x)
{
int t;
t=rs[x];
rs[x]=ls[t];
ls[t]=x;
size[t]=size[x];
up(x);
x=t;
}
void insert_sum(int x,int &i)
{
if(!i)
{
i=++tot;
w[i]=size[i]=1;
v[i]=x;
r[i]=rand();
return ;
}
size[i]++;
if(x==v[i])
{
w[i]++;
}
else if(x>v[i])
{
insert_sum(x,rs[i]);
if(r[rs[i]]<r[i])
{
lturn(i);
}
}
else
{
insert_sum(x,ls[i]);
if(r[ls[i]]<r[i])
{
rturn(i);
}
}
return ;
}
void delete_sum(int x,int &i)
{
if(i==0)
{
return ;
}
if(v[i]==x)
{
if(w[i]>1)
{
w[i]--;
size[i]--;
return ;
}
if((ls[i]*rs[i])==0)
{
i=ls[i]+rs[i];
}
else if(r[ls[i]]<r[rs[i]])
{
rturn(i);
delete_sum(x,i);
}
else
{
lturn(i);
delete_sum(x,i);
}
return ;
}
size[i]--;
if(v[i]<x)
{
delete_sum(x,rs[i]);
}
else
{
delete_sum(x,ls[i]);
}
return ;
}
int ask_num(int x,int i)
{
if(i==0)
{
return 0;
}
if(v[i]==x)
{
return size[ls[i]]+1;
}
if(v[i]<x)
{
return ask_num(x,rs[i])+size[ls[i]]+w[i];
}
return ask_num(x,ls[i]);
}
int ask_sum(int x,int i)
{
if(i==0)
{
return 0;
}
if(x>size[ls[i]]+w[i])
{
return ask_sum(x-size[ls[i]]-w[i],rs[i]);
}
else if(size[ls[i]]>=x)
{
return ask_sum(x,ls[i]);
}
else
{
return v[i];
}
}
void ask_front(int x,int i)
{
if(i==0)
{
return ;
}
if(v[i]<x)
{
answer=i;
ask_front(x,rs[i]);
return ;
}
else
{
ask_front(x,ls[i]);
return ;
}
return ;
}
void ask_back(int x,int i)
{
if(i==0)
{
return ;
}
if(v[i]>x)
{
answer=i;
ask_back(x,ls[i]);
return ;
}
else
{
ask_back(x,rs[i]);
return ;
}
}
int main()
{
srand(12378);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
answer=0;
scanf("%d%d",&opt,&x);
if(opt==1)
{
insert_sum(x,root);
}
else if(opt==2)
{
delete_sum(x,root);
}
else if(opt==3)
{
printf("%d\n",ask_num(x,root));
}
else if(opt==4)
{
printf("%d\n",ask_sum(x,root));
}
else if(opt==5)
{
ask_front(x,root);
printf("%d\n",v[answer]);
}
else if(opt==6)
{
ask_back(x,root);
printf("%d\n",v[answer]);
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号