混合高斯模型

玩了混合高斯模型，先转几个参考资料，曾经试过自己写代码，结果发现混合高斯模型矩阵运算对我的计算能力要求很高，结果失败了，上网找了代码学习一下大牛们的编程思想，事实证明数学写出来的公式虽然很美，但是现实写代码的时候要考虑各种问题~~~

1.http://www.cnblogs.com/cfantaisie/archive/2011/08/20/2147075.html （主要实现代码）

2.http://freemind.pluskid.org/machine-learning/regularized-gaussian-covariance-estimation/ （对于奇异矩阵的正则化）

3.参考的一本书，Computer Vision Models, Learning, and Inference.（数学推导）

4.斯坦福机器学习课程（数学推导）

利用EM算法：

E-step：

 

 

 

 

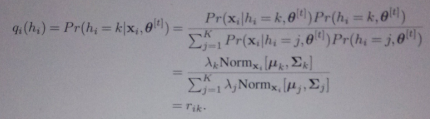
M-step:

 

 

 

 

 

 

 

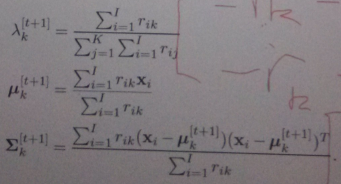
matlab实现代码：

function prob = MOF_guassPdf(Data,Mu,Sigma)
%

% 根据高斯分布函数计算每组数据的概率密度 Probability Density Function (PDF) 

% 输入 -----------------------------------------------------------------

%   o Data:  D x N ，N个D维数据

%   o Mu:    D x 1 ，M个Gauss模型的中心初始值

%   o Sigma: D x D ，每个Gauss模型的方差（假设每个方差矩阵都是对角阵，

%                                   即一个数和单位矩阵的乘积）

% Outputs ----------------------------------------------------------------

%   o prob:  N x 1 array representing the probabilities for the 

%            N datapoints.     

[dim,N] = size(Data);

Data = Data' - repmat(Mu',N,1);

prob = sum((Data/Sigma).*Data, 2);

prob = exp(-0.5*prob) / sqrt((2*pi)^dim * (abs(det(Sigma))+realmin));

EM迭代：

function [Alpha, Mu, Sigma] = MOF_EM(Data, Alpha0, Mu0, Sigma0)
%% EM 迭代停止条件
loglik_threshold = 1e-10;

%% 初始化参数

[dim, N] = size(Data); 

M = size(Mu0,2);

loglik_old = -realmax;

nbStep = 0;
                %Data是D*N的矩阵

Mu = Mu0;       %Mu是D*M的矩阵

Sigma = Sigma0; %sigma是D*D*M的三维矩阵

Alpha = Alpha0; %alpha是1*M大小的向量，意思是列代表第M个高斯模型。

Epsilon = 0.0001; 

while (nbStep < 1200)

  nbStep = nbStep+1;

  %% E-步骤 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

  for i=1:M

    % PDF of each point

    Pxi(:,i) = MOF_guassPdf(Data, Mu(:,i), Sigma(:,:,i));          

  end

  

  % 计算后验概率 beta(i|x)

  Pix_tmp = repmat(Alpha,[N 1]).*Pxi; %Pxi应该是N*M的高斯概率矩阵，意思是第N个数据计算第M个高斯函数的概率

  Pix = Pix_tmp ./ (repmat(sum(Pix_tmp,2),[1 M])+realmin);

  Beta = sum(Pix);

  %% M-步骤 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

  for i=1:M

    % 更新权值

    Alpha(i) = Beta(i) / N;

    % 更新均值

    Mu(:,i) = Data*Pix(:,i) / Beta(i);

    % 更新方差

    Data_tmp1 = Data - repmat(Mu(:,i),1,N);

    Sigma(:,:,i) = (repmat(Pix(:,i)',dim, 1) .* Data_tmp1 * Data_tmp1') / Beta(i);

    %% Add a tiny variance to avoid numerical instability

    Sigma(:,:,i) = Sigma(:,:,i) + 1E-5.*diag(ones(dim,1));

  end

 

%  %% Stopping criterion 1 %%%%%%%%%%%%%%%%%%%%

  for i=1:M

    %Compute the new probability p(x|i)

    Pxi(:,i) = MOF_guassPdf(Data, Mu(:,i), Sigma(i));

  end

  %Compute the log likelihood

  F = Pxi*Alpha';

  F(find(F<realmin)) = realmin;

  loglik = mean(log(F));

  %Stop the process depending on the increase of the log likelihood 

  if abs((loglik/loglik_old)-1) < loglik_threshold

    break;

  end

  loglik_old = loglik;

 

  %% Stopping criterion 2 %%%%%%%%%%%%%%%%%%%%
%{
  v = [sum(abs(Mu - Mu0)), abs(Alpha - Alpha0)];

  s = abs(Sigma-Sigma0);

  v2 = 0;

  for i=1:M

    v2 = v2 + det(s(:,:,i));

  end

 

  if ((sum(v) + v2) < Epsilon)

    break;

  end

  Mu0 = Mu;

  Sigma0 = Sigma;

  Alpha0 = Alpha;
%}
end

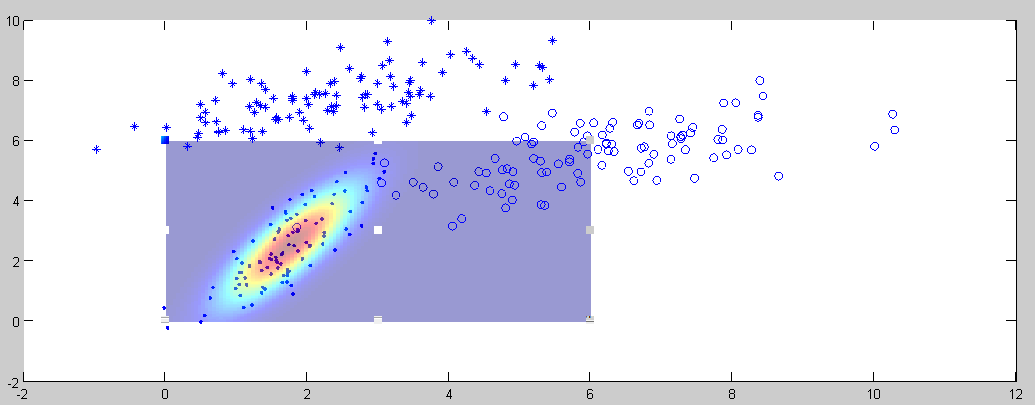
测试结果

编写代码随机生成3个高斯分布的数据，参数也随机生成（注意sigma要半正定对称）：

这里只画了一个经过EM算法迭代所得参数的高斯函数图..（有点丑，不知道怎么将mesh弄透明，求搜索关键词）。