转：遗传算法解决TSP问题

1.编码

这篇文章中遗传算法对TSP问题的解空间编码是十进制编码。如果有十个城市，编码可以如下：

0 1 2 3 4 5 6 7 8 9

这条编码代表着一条路径，先经过0，再经过1，依次下去。

2.选择

选择操作仍然是轮盘赌模型，虽然不会出现路径长度为负数的情况，但是需要考虑与上篇文章不同的是求的是最小值。因此在代码中概率的计算为：

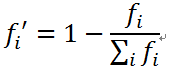
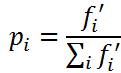
3.交叉

4.变异

变异操作就是交换两个城市，例如：

0 1 2 3 4

0 2 1 3 4

 

5.代码实现

 

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<math.h>
#include<time.h>
#include<Windows.h>
#include<fstream>
#include<iostream>
using namespace std;

const int cities = 10;  //城市的个数
const int MAXX = 100;   //迭代次数
const double pc = 0.8;  //交配概率
const double pm = 0.05; //变异概率
const int num = 10;  //种群的大小

int bestsolution;//最优染色体
double distance1[cities][cities];//城市之间的距离

struct group  //染色体的结构
{
    int city[cities];//城市的顺序
    double adapt;//适应度
    double p;//在种群中的幸存概率
}group[num],grouptemp[num];

struct point{
    double x,y;
}Cpoint[cities];

//随机产生cities个城市之间的相互距离
void init()
{/*
    int i,j;
    memset(distance,0,sizeof(distance));
    srand((unsigned)time(NULL));
    for(i=0;i<cities;i++)
    {
        for(j=i+1;j<cities;j++)
        {
           distance[i][j]=rand()%100;
           distance[j][i]=distance[i][j];
        }
    }
    //打印距离矩阵
    printf("城市的距离矩阵如下\n");
    for(i=0;i<cities;i++)
    {
        for(j=0;j<cities;j++)
        printf("%4d",distance[i][j]);
        printf("\n");
    }*/
    ifstream f1("C:\\city.txt",ios::in);
    for(int i = 0; i < cities; i++){
        //if(ll % 2 != 0)
            f1 >> Cpoint[i].x;
        //if(ll % 2 == 0)
            f1 >> Cpoint[i].y;
        //ll++;
    }
    f1.close();
    double tmp1 = 0.0;
    for(int m = 0; m < cities; m++){
        for(int n = 0; n < cities; n++){
            if(m == n)
                distance1[m][n] = 0;
            else{
                tmp1 = sqrt(pow(Cpoint[m].x - Cpoint[n].x,2) + pow(Cpoint[m].y - Cpoint[n].y,2));
                distance1[m][n] = tmp1;
                distance1[n][m] = tmp1;
            }
        }
    }
    //打印距离矩阵
    printf("城市的距离矩阵如下\n");
    for(int i = 0; i < cities; i++)
    {
        for(int j = 0; j<cities; j++){
            cout << distance1[i][j] << ' ';
        }
        cout << endl;
    }
}
//随机产生初试群
void groupproduce()
{
    int i,j,t,k,flag;

    for(i = 0; i < num; i++)  //初始化
        for(j = 0; j < cities; j++)
            group[i].city[j]=-1;

    srand((unsigned)time(NULL));
    for(i = 0; i < num; i++)
    {
        //产生10个不相同的数字
        for(j = 0; j < cities;)
        {
            t = rand() % cities;
            flag = 1;
            for(k = 0; k < j; k++)
            {
                if(group[i].city[k] == t)
                {
                    flag = 0;
                    break;
                }
            }
            if(flag)
            {
                group[i].city[j] = t;
                j++;
            }
        }
    }
    //打印种群基因
    printf("初始的种群\n");
    for(i = 0; i < num; i++)
    {
        for(j = 0; j < cities; j++)
            printf("%4d",group[i].city[j]);
        printf("\n");
    }
}
//评价函数,找出最优染色体
void pingjia()
{
    int i,j;
    int n1,n2;
    double sumdistance;
    int biggestsum = 0;
    double biggestp = 0;
    for(i = 0; i < num; i++)
    {
        sumdistance = 0;
        for(j = 1; j < cities; j++)
        {
            n1 = group[i].city[j-1];
            n2 = group[i].city[j];
            sumdistance += distance1[n1][n2];
        }
        sumdistance += distance1[group[i].city[cities-1]][group[i].city[0]];
        group[i].adapt = sumdistance; //每条染色体的路径总和
        //printf("%d",group[i].adapt);
        biggestsum += sumdistance; //种群的总路径
    }
    //计算染色体的幸存能力,路劲越短生存概率越大
    for(i = 0; i < num; i++)
    {
        group[i].p = 1 - (double)group[i].adapt / (double)biggestsum; 
        
        biggestp += group[i].p;
        //printf("%s","  ");
    }
    //printf("%f",biggestp);
    for(i = 0; i < num; i++){
        
        group[i].p = group[i].p / biggestp;

    }//在种群中的幸存概率,总和为1
    //求最佳路径

    bestsolution = 0;
    for(i = 0;i < num; i++)
        if(group[i].p > group[bestsolution].p)
            bestsolution = i;
    //打印适应度
    /*for(i = 0; i < num; i++)
        cout << "染色体" << i << "的路径之和与生存概率分别为" << group[i].adapt << "和" << group[i].p;
        //printf("染色体%d的路径之和与生存概率分别为%4d  %.4f\n",i,group[i].adapt,group[i].p);
    cout << "当前种群的最优染色体是" << bestsolution << "号染色体" << endl;
    //printf("当前种群的最优染色体是%d号染色体\n",bestsolution);*/
}
//选择
void xuanze()
{
    int i,j,temp;
    double gradient[num];//梯度概率
    double xuanze[num];//选择染色体的随机概率
    int xuan[num];//选择了的染色体
    //初始化梯度概率
    for(i = 0; i < num; i++)
    {
        gradient[i] = 0.0;
        xuanze[i] = 0.0;
    }
    gradient[0] = group[0].p;

    for(i = 1; i < num; i++)
        gradient[i] = gradient[i-1]+group[i].p;

    srand((unsigned)time(NULL));
    //随机产生染色体的存活概率
    for(i = 0; i < num; i++)
    {
        xuanze[i] = (rand()%100);
        xuanze[i] /= 100;
    }
    //选择能生存的染色体
    for( i = 0; i < num; i++)
    {
        for(j = 0; j < num; j++)
        {
            if(xuanze[i] < gradient[j])
            {
                xuan[i] = j; //第i个位置存放第j个染色体
                break;
            }
        }
    }
    //拷贝种群
    for(i = 0; i < num; i++)
    {
        grouptemp[i].adapt = group[i].adapt;
        grouptemp[i].p = group[i].p;
        for(j = 0; j < cities; j++)
        grouptemp[i].city[j] = group[i].city[j];
    }
    //数据更新
    for(i = 0; i < num; i++)
    {
        temp = xuan[i];
        group[i].adapt = grouptemp[temp].adapt;
        group[i].p = grouptemp[temp].p;
        for(j = 0; j < cities; j++)
            group[i].city[j] = grouptemp[temp].city[j];
    }
    //用于测试
    /*
    printf("<------------------------------->\n");
    for(i=0;i<num;i++)
    {
        for(j=0;j<cities;j++)
        printf("%4d",group[i].city[j]);
        printf("\n");
        printf("染色体%d的路径之和与生存概率分别为%4d  %.4f\n",i,group[i].adapt,group[i].p);
    }
    */
}

//交配,对每个染色体产生交配概率,满足交配率的染色体进行交配  
void  jiaopei()  
{  
    int i,j,k,kk;  
    int t;//参与交配的染色体的个数  
    int point1,point2,temp;//交配断点  
    int pointnum;  
    int temp1,temp2;  
    int map1[cities],map2[cities];  
    double jiaopeip[num];//染色体的交配概率  
    int jiaopeiflag[num];//染色体的可交配情况  
    int kkk,flag=0;  
    //初始化  
    for(i = 0; i < num; i++)  
    {  
        jiaopeiflag[i] = 0;  
    }  
    //随机产生交配概率  
    srand((unsigned)time(NULL));  
    for(i = 0; i < num; i++)  
    {  
        jiaopeip[i] = (rand()%100);  
        jiaopeip[i] /= 100;  
    }  
    //确定可以交配的染色体  
    t = 0;  
    for(i = 0; i < num; i++)  
    {  
        if(jiaopeip[i] < pc)  
        {  
            jiaopeiflag[i] = 1;  
            t++;  
        }  
    }  
    t = t/2 * 2;//t必须为偶数,产生t/2个0-9交配断点  
    srand((unsigned)time(NULL));  
    temp1 = 0;     //temp1号染色体和temp2染色体交配  
    for(i = 0; i < t/2; i++)  //如果有5个染色体需要交配，但是实际上t/2代表只有4个染色体会真正的交配，剩下的1个再加上5个不需要交配的染色体直接进入下一代。
    {  
        point1 = rand() % cities;//交配点1  
        point2 = rand() % cities;//交配点2  
        //选出一个需要交配的染色体1  
        for(j = temp1;j < num; j++)  
        {  
            if(jiaopeiflag[j] == 1)  
            {  
                temp1 = j;  
                break;  
            }  
        }  
        //选出另一个需要交配的染色体2与1交配  
        for(j = temp1+1; j < num; j++)  
        {  
            if(jiaopeiflag[j] == 1)  
            {  
                temp2 = j;  
                break;  
            }  
        }  
        //进行基因交配  
        if(point1 > point2) //保证point1<=point2  
        {  
            temp = point1;  
            point1 = point2;  
            point2 = temp;  
        }  
        //初始化  
        memset(map1,-1,sizeof(map1));  
        memset(map2,-1,sizeof(map2));  
        //断点之间的基因产生映射  
        for(k = point1; k <= point2; k++)  
        {  
            map1[group[temp1].city[k]] = group[temp2].city[k];  
            map2[group[temp2].city[k]] = group[temp1].city[k];  
        }  
        //断点两边的基因互换  
        for(k = 0; k < point1; k++)  
        {  
            temp = group[temp1].city[k];  
            group[temp1].city[k] = group[temp2].city[k];  
            group[temp2].city[k] = temp;  
        }  
        for(k = point2+1; k < cities; k++)  
        {  
            temp = group[temp1].city[k];  
            group[temp1].city[k] = group[temp2].city[k];  
            group[temp2].city[k] = temp;  
        }  
        //printf("处理冲突---------------------\n");  
        //处理染色体1产生的冲突基因  
        for(k = 0; k < point1; k++)  
        {  
            for(kk = point1; kk <= point2; kk++)  
            {  
                if(group[temp1].city[k] == group[temp1].city[kk])  
                {  
                    group[temp1].city[k] = map1[group[temp1].city[k]];  //如果相等则进行映射操作
                    //find  
                    for(kkk = point1;kkk <= point2; kkk++)  
                    {  
                        if(group[temp1].city[k] == group[temp1].city[kkk])  //考虑如果映射一次仍然具有相同的城市，则再进行一次映射操作
                        {  
                            flag = 1;  
                            break;  
                        }  
                    }  
                    if(flag == 1)  //flag不断判断同一染色体中是否还存在相同的城市
                    {  
                        kk = point1 - 1;  
                        flag = 0;  
                    }  
                    else  
                    {  
                        flag = 0;  
                        break;  
                    }  
                }  
            }  
              
        }  
        for(k = point2+1; k < cities; k++)  
        {  
            for(kk = point1; kk <= point2; kk++)  
            {  
                if(group[temp1].city[k] == group[temp1].city[kk])  
                {  
                    group[temp1].city[k] = map1[group[temp1].city[k]];  
                    //find  
                    for(kkk = point1;kkk <= point2; kkk++)  
                    {  
                        if(group[temp1].city[k] == group[temp1].city[kkk])  
                        {  
                            flag = 1;  
                            break;  
                        }  
                    }  
                    if(flag == 1)  
                    {  
                        kk = point1 - 1;  
                        flag = 0;  
                    }  
                    else  
                    {  
                        flag = 0;  
                        break;  
                    }  
                }  
            }  
        }  
        //处理2染色体产生的冲突基因  
        for(k = 0;k < point1; k++)  
        {  
            for(kk = point1; kk <= point2; kk++)  
            {  
                if(group[temp2].city[k] == group[temp2].city[kk])  
                {  
                    group[temp2].city[k] = map2[group[temp2].city[k]];  
                    //find  
                    for(kkk = point1;kkk <= point2; kkk++)  
                    {  
                        if(group[temp2].city[k] == group[temp2].city[kkk])  
                        {  
                            flag = 1;  
                            break;  
                        }  
                    }  
                    if(flag == 1)  
                    {  
                        kk = point1 - 1;  
                        flag = 0;  
                    }  
                    else  
                    {  
                        flag = 0;  
                        break;  
                    }  
                }  
            }  
        }  
        for(k = point2+1; k < cities; k++)  
        {  
            for(kk = point1; kk <= point2; kk++)  
            {  
                if(group[temp2].city[k] == group[temp2].city[kk])  
                {  
                    group[temp2].city[k] = map2[group[temp2].city[k]];  
                    //find  
                    for(kkk = point1; kkk <= point2; kkk++)  
                    {  
                        if(group[temp2].city[k] == group[temp2].city[kkk])  
                        {  
                            flag = 1;  
                            break;  
                        }  
                    }  
                    if(flag == 1)  
                    {  
                        kk = point1 - 1;  
                        flag = 0;  
                    }  
                    else  
                    {  
                        flag = 0;  
                        break;  
                    }  
                }  
            }  
        }  
        temp1 = temp2 + 1;  
    }  
}


void bianyi()
{
    int i,j;
    int t;
    int temp1,temp2,point;
    double bianyip[num]; //染色体的变异概率
    int bianyiflag[num];//染色体的变异情况
    for(i = 0;i < num; i++)//初始化
    bianyiflag[i]=0;
    //随机产生变异概率
    srand((unsigned)time(NULL));
    for(i = 0; i < num; i++)
    {
        bianyip[i] = (rand()%100);
        bianyip[i] /= 100;
    }
    //确定可以变异的染色体
    t=0;
    for(i = 0; i < num; i++)
    {
        if(bianyip[i] < pm)
        {
            bianyiflag[i] = 1;
            t++;
        }
    }
    //变异操作,即交换染色体的两个节点
    srand((unsigned)time(NULL));
    for(i = 0; i < num; i++)
    {
        if(bianyiflag[i] == 1)
        {
            temp1 = rand() % 10;
            temp2 = rand() % 10;
            point = group[i].city[temp1];
            group[i].city[temp1] = group[i].city[temp2];
            group[i].city[temp2] = point;
        }
    }
}
int main()
{
    int i,j,t;
    init();
    groupproduce();
    //初始种群评价
    pingjia();
    t=0;
    while(t++ < MAXX)
    {
         xuanze();
         jiaopei();
         bianyi();
         pingjia();
    }
    //最终种群的评价
    printf("\n输出最终的种群评价\n");
    for(i = 0; i < num; i++)
    {
        for(j = 0;j < cities; j++)
        {
            printf("%4d",group[i].city[j]);
        }
        cout << "   adapt:" << group[i].adapt << "   p:" << group[i].p << endl;
        //printf("  adapt:%4d, p:%.4f\n",group[i].adapt,group[i].p);
    }
    printf("最优解为%d号染色体\n",bestsolution);
    system("pause");
    return 0;
}

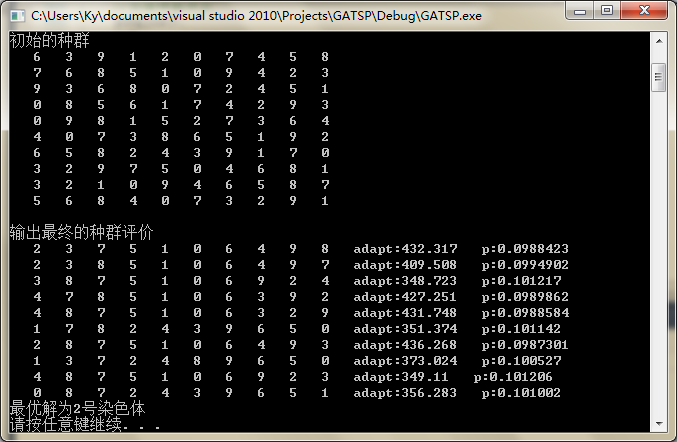
6.结果显示

我的城市为10个，坐标为

41 94
37 84
53 67
25 62
7 64
2 99
68 58
71 44
54 62
83 69

输出结果如图：

7.参考

1.http://blog.csdn.net/mylovestart/article/details/8977005#cpp

2.http://blog.csdn.net/yeruby/article/details/13161853