DS博客作业02--栈和队列
0.PTA得分截图

1.本周学习总结
1.1 1.1 总结栈和队列内容
-
栈的存储结构及操作:
-
栈的存储结构:和顺序表和链表一样,栈也是用来存储逻辑关系为一对一数据的线性存储结构;但不同的是,栈只在一端进行插入和删除操作,及所谓的进栈出栈,而且出栈顺序为先进后出,后进先出。可以把栈看成一个羽毛球筒或乒乓球筒,拿出来的第一个球一定是最后一个放进去的,而对于第一个放进去的球,只有等其他的球都拿出来时才能拿到,这就是先进后出,后进先出。具体示意图如下:
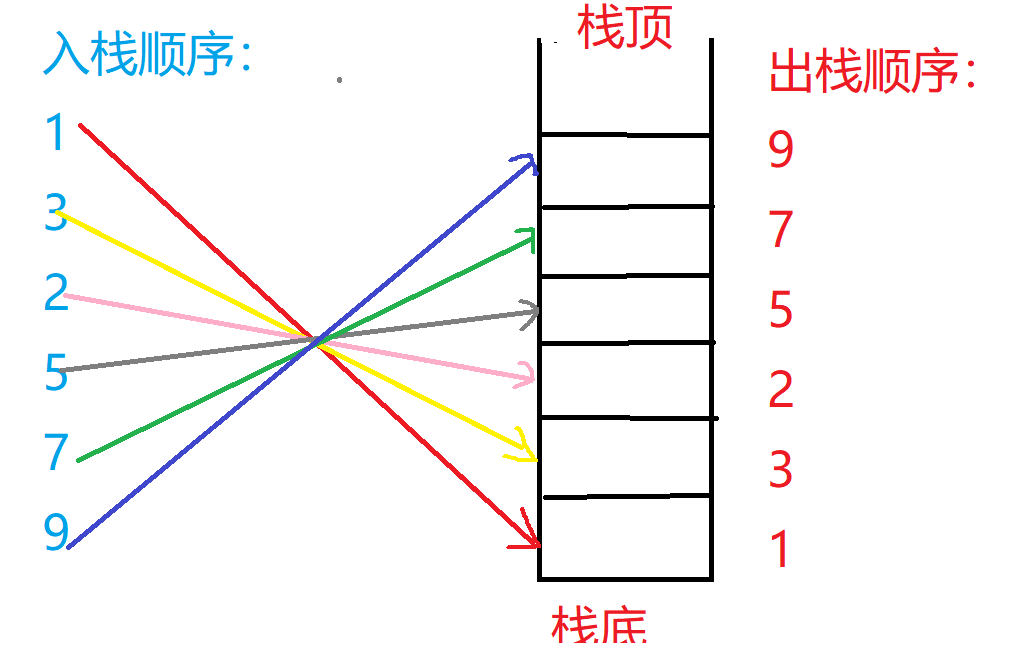
-
栈的基本操作:对于栈的使用,可以直接调用STL容器
stack,但使用时必须包含#include<stack>头文件。其有以下几个基本操作:- empty():测试栈是否为空,如果为空的话返回
true,否则返回false。 - size():返回栈中元素个数。
- top():返回栈顶元素,即最后push进来的那个元素。
- push():压一个值到栈中,即进栈操作。
- pop():将栈顶元素弹出,即出栈。但是这个函数没有返回值!!!所以如果要获取栈顶元素应该先调用top(),再pop()。
- swap():将两个
stack的内容进行交换,前提是这两个stack的存储的元素类型以及底层采用的基础容器类型都必须相同!有两种用法。例如x.swap(y)和swap(x,y)都是将x,y栈的内容进行交换。 - emplace(Args...):功能上与 push相同。不过emplace更高效。arg... 可以是一个参数,也可以是多个参数,但它们都只用于构造一个对象,并在栈顶直接生成该对象,作为新的栈顶元素。
- empty():测试栈是否为空,如果为空的话返回
-
-
栈的应用:
- 递归:由于递归过程的退回顺序是其前行顺序的逆序,符合栈的存储方式。简单的说,就是在每次递归后将函数的局部变量、参数值以及返回地址压入栈中,在退回阶段,位于栈顶的局部变量、参数值和返回地址被弹出,用于返回调用层次中执行代码的其余部分,也就是恢复了调用的状态。
- 进制转换:由于计算机中存储的数据都是二进制,所以在使用时往往需要把十进制转换成二进制,其转换方法就是将十进制数除2然后倒序取余数,正好符合栈先进后出、后进先出的特点,所以可以用栈来实现进制的转换。
- 符号匹配:可以用来判断一个表达式中的符号是否相互匹配。如
(和),遇到(,则入栈,遇到)则从栈顶弹出(与之配对。当整个表达式扫描完时,如果栈为空,说明表达式中所有的括号都成功匹配完成;如果栈不空,说明栈内仍有(,也就是(多余;如果扫描到)时,栈空或者栈顶元素不是(,则说明表达式中)是多余的。 - 中缀表达式转后缀表达式:输入一串表达式并依次扫描。如果是操作数的话,就
push入栈,如果是运算符且当前运算符优先级比栈顶元素高,则push入栈,否则将栈顶元素pop出栈直到栈顶运算符的优先级小于当前运算符。扫描完整个表达式后,判断栈是否为空,如果不为空的话则将剩余元素全部出栈。
-
队列的存储结构及操作:
-
队列的存储结构:队列同栈一样,也是一种运算受限制的线性表。队列只允许在一端进行插入,而在另一端进行删除。其中,把插入数据的一端称为队尾,删除数据的一端称为队首。向队尾插入元素称为进队或入队,新元素入队后成为新的队尾元素;从队列中删除元素称为离队或出队,元素出队后,其后续元素成为新的队首元素。由于队列的这种操作方式,所以不同于栈的进出顺序,队列是先进先出。
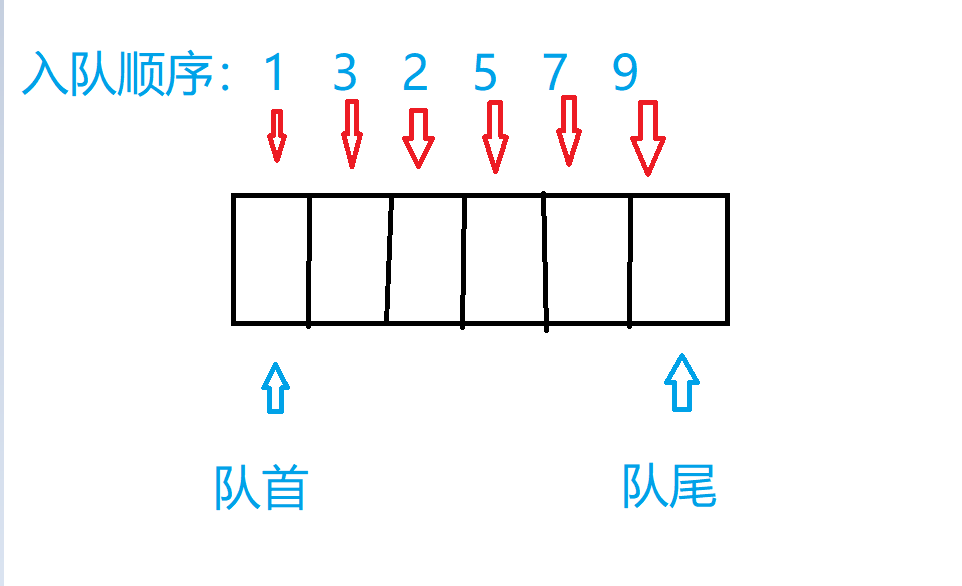
-
队列的基本操作:对于队列的使用,可以直接调用STL容器
queue,使用时必须包含#include<queue>头文件。其有以下几个基本操作:- empty():判断队列是否为空,如果为空则返回
true,否则返回false。 - size():返回队列中元素的个数。
- front():返回队首元素,即
front指针所指的元素。 - back():返回队尾元素,即
rear指针所指的元素。 - push():在队尾插入一个元素。
- pop():删除队首元素。
- empty():判断队列是否为空,如果为空则返回
-
-
队列的应用:
- 排队问题:生活中遇到的与排队有关的问题其本上都可以看成队列。例如银行业务办理排队:先到先办理,上一个办理完后下一个即队首接上,继续办理。当
front==rear时,队空,即所有人都办理完成。 - 迷宫问题:从入口块开始,往下寻找可走的方块,然后入栈并记录上一块方块的位置,直到找到出口为止。然后从出口方块开始,逆序往回寻找入口方块。用队列来解决迷宫问题可以找到最短路径。
- 循环队列-约瑟夫环:将顺序队列的队首队尾相接就变成了一个循环队列。从队首开始往下报数,当报到指定数字时,该位置的人出列,然后下一个人从1开始重新报数,依次类推。通过循环队列的结构特点可以用来解决约瑟夫环的问题。详见
pta 7-6 jmu-报数游戏.
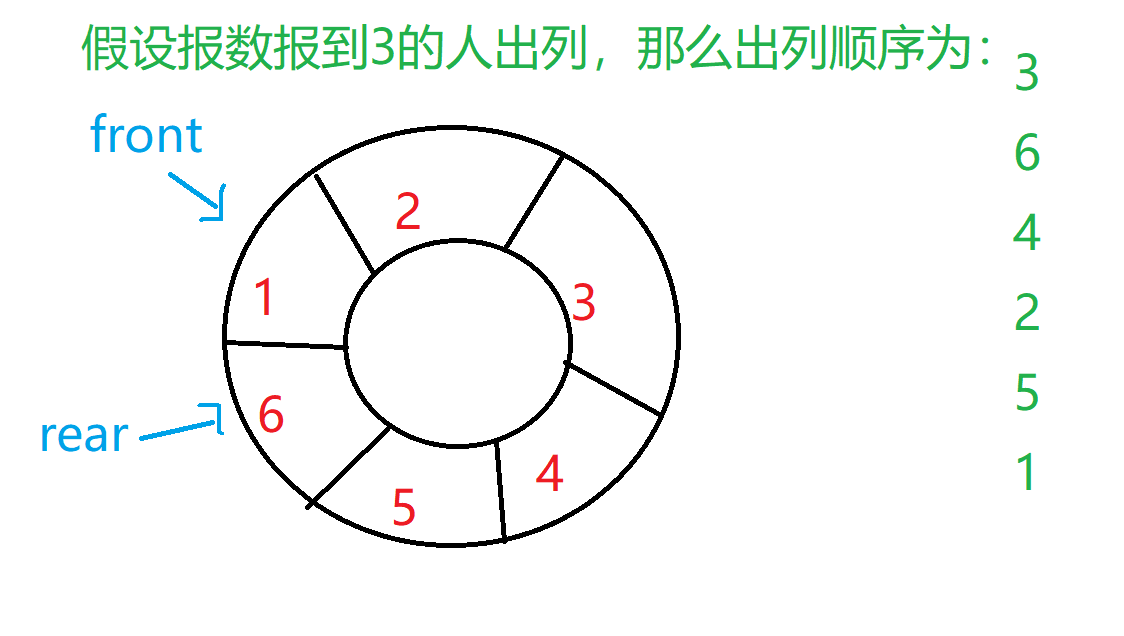
- 排队问题:生活中遇到的与排队有关的问题其本上都可以看成队列。例如银行业务办理排队:先到先办理,上一个办理完后下一个即队首接上,继续办理。当
1.2.谈谈你对栈和队列的认识及学习体会。
- 栈可分为顺序栈和链栈。顺序栈类似于数组,找数据的时候方便快捷,增删数据的时候就比较麻烦,但由于不知道数据的个数,所以容易造成内存浪费。链栈类似于链表,在增删数据操作时方便快捷,当插入数据时再临时开辟一块空间,所以不会造成内存浪费;缺点也和链表一样,找数据的时候比较麻烦,需要遍历整条链。总的来说,栈就像是一个单向开口的乒乓球筒,先放进去的球只有在最后的时候才能拿的出来,而最后放进去的球一定是最先拿出来的。
- 队列可分为顺序队列和循环队列。顺序队列就像是一条双向的水管,只能从一端进水,另一端出水,即先进先出;而循环队列就是将这条水管的两端连接起来。
- 学习体会:由于栈和队列在编译器中有STL容器,使用时只需要加上
头文件即可使用,所以用起来非常方便。而且栈和队列可以用来解决生活中许多常见的问题,因此泛用性比较广。但是对于不同类型的栈和队列,判断空和满的条件不一样,所以在写代码的过程中很容易出错,需要擦亮眼睛仔细看。
2.PTA实验作业
2.1 7-6 jmu-报数游戏
2.1.1代码截图

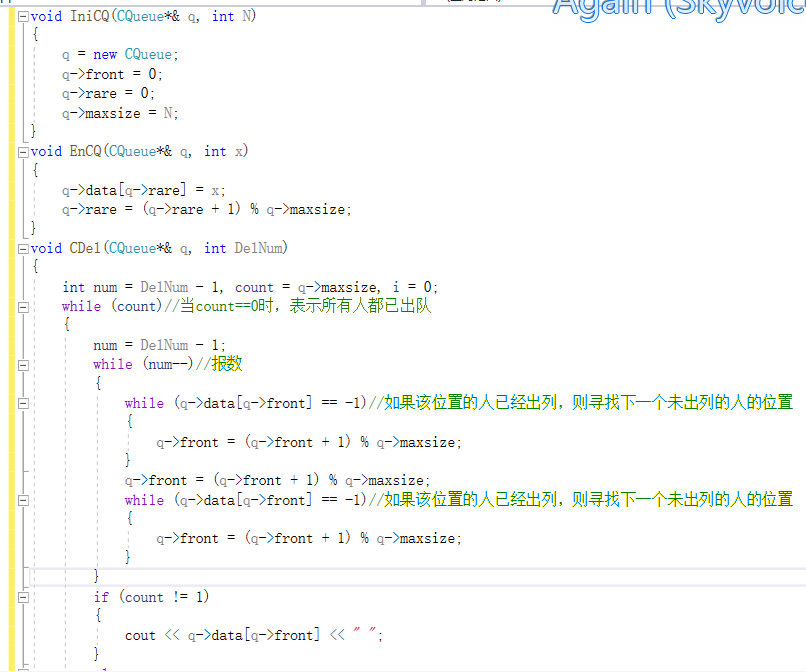
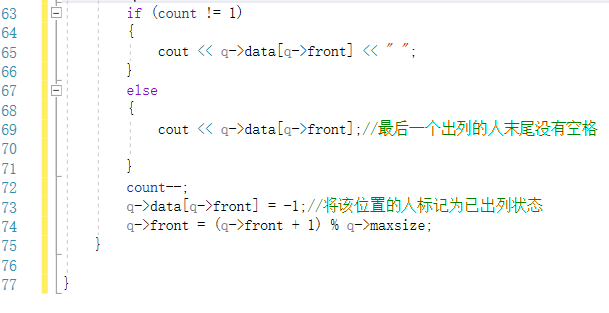
2.1.2本题PTA提交列表说明。
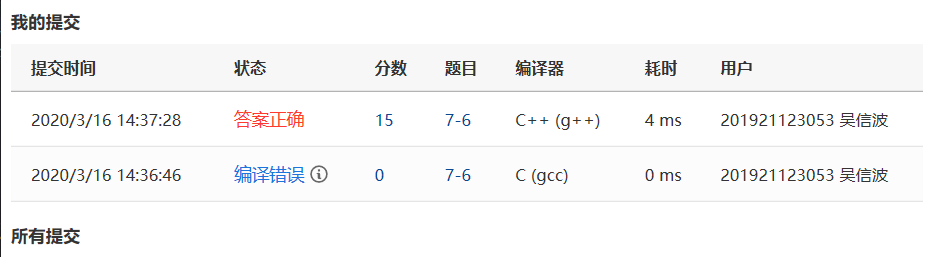
编译错误:这题我是在VS调试能运行后才提交到pta的,编译错误是因为pta默认编译语言是C,而我用的是c++。
答案正确:这里就说一下我在VS调试过程中遇到的问题吧。
1.初始化循环队列的时候一直在纠结要不要让front指向第一个节点的前一个位置,也就是多设一个空节点,加上对队列还是不够熟悉,导致要么漏插一个元素,要么栈溢出,还有就是front和rare指针的移动忘记考虑其范围,导致循环队列溢出。于是便去再次了解一下循环队列及其结构特点后解决问题。
2.在报数出列过程中,忘记判断当前位置是否还有人,即当前位置的元素是否为-1,导致输出出错,且循环报数。在报数过程中加上两条while语句分别对报数前和报数后所在位置元素进行判断后解决问题。
2.2 7-9 银行排队问题之单窗口“夹塞”版
2.2.1代码截图
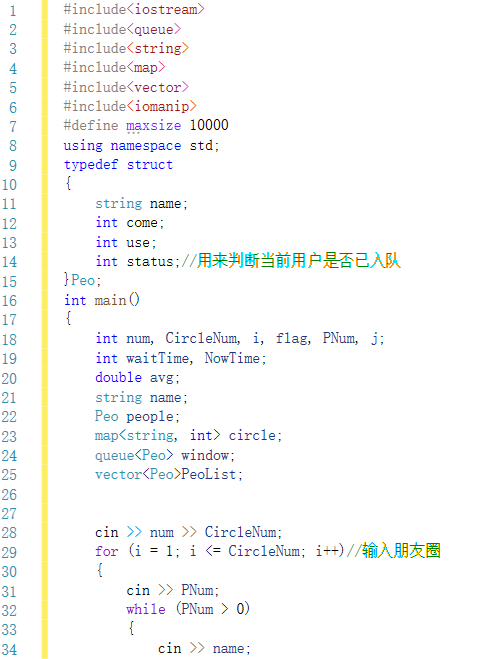
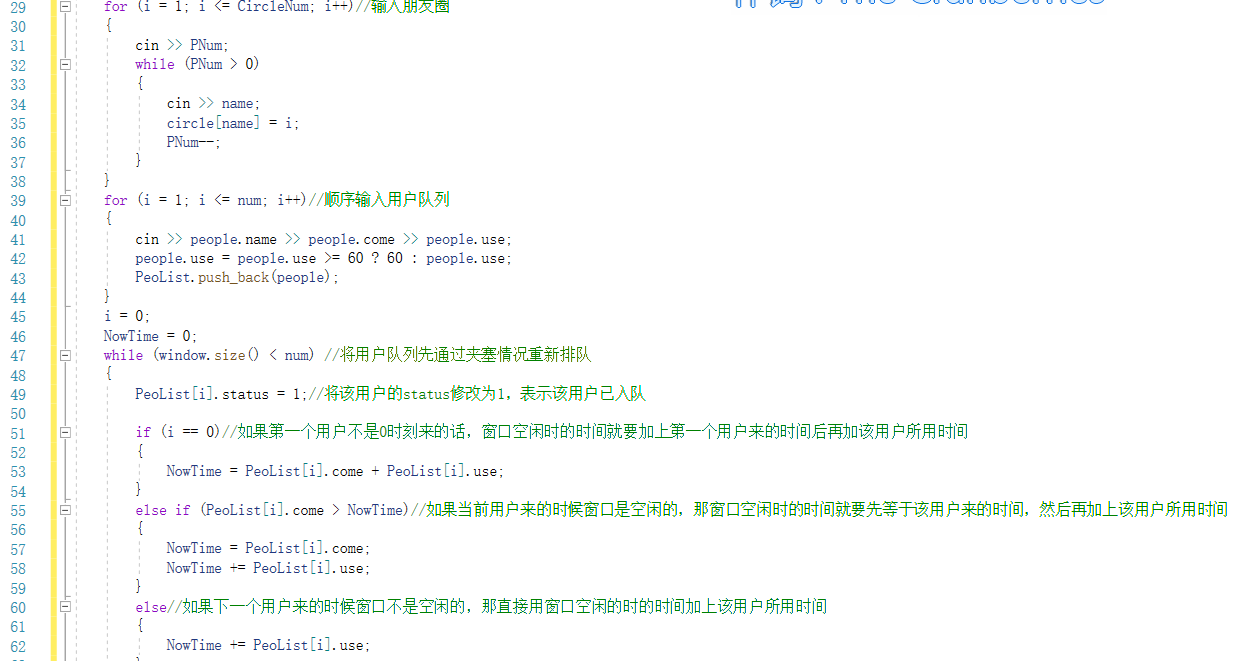

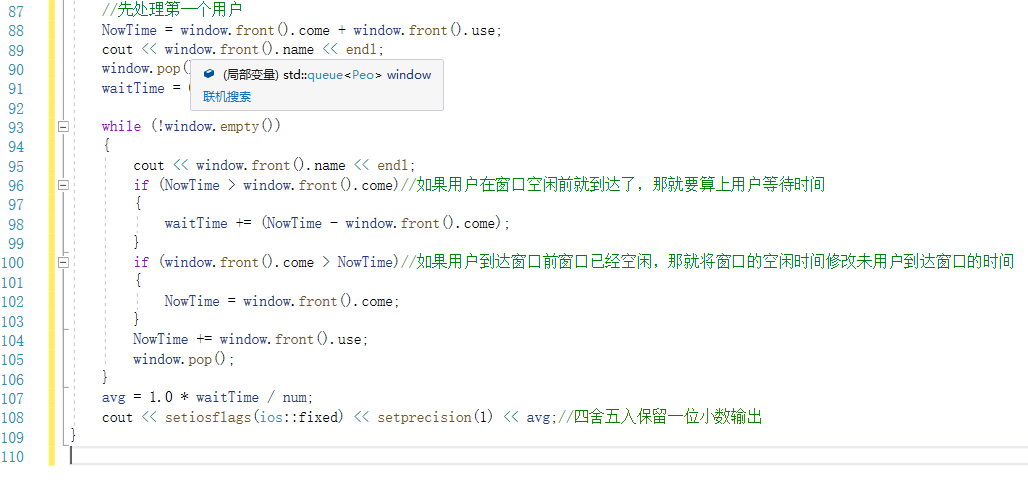
2.2.2本题PTA提交列表说明。

编译错误1-2、运行超时:一开始毫无头绪,于是便想看一下题目的测试点有什么,就随便写了几行代码。
部分正确3-7:当我写完程序的大体功能后,题目所给样例测试点也过了,但提交却还有两个测试点过不了:`窗口有完全空闲一段时间,等待下一位`:这个测试点过不了是因为我在这种情况下修改窗口空闲时间为用户到达时间后忘记加上用户所办理的时间;`刚好朋友处理完自己的事务,不用等待就夹塞;到达时朋友已经走了,只好排队`:这个测试点过不了是以为在排序夹塞后的队列时,忘记判断用户的朋友在用户办理完成之前是否已经到达。
部分正确8:修改了上诉错误后,发现`刚好朋友处理完自己的事务,不用等待就夹塞;到达时朋友已经走了,只好排队`这个测试点还是过不了,经检查后发现,来的时候刚好朋友处理完自己的事物的那条判断语句应该用`PeoList[j].come <= NowTime`,而我原本是只有小于号。
答案正确9-11:修改完上述错误后,所有测试点都通过了。
3.阅读代码
3.1 题目及解题代码
#include <iostream>
#include <fstream>
#include <stack>
#include <vector>
using namespace std;
int main()
{
int total;
string instr, outstr;
stack<int> s;
cin >> total;
cin >> instr;
cin >> outstr;
vector<int> vin, vout;
for(int i = 0; i < instr.size(); i++)//设置入栈序列
{
int num = instr[i] - '0';
vin.push_back(num);
}
for(int i = 0; i < outstr.size(); i++)//设置出栈序列
{
int num = outstr[i] - '0';
vout.push_back(num);
}
int i = 0, j = 0;
for(; i < total; i++)
{
s.push(vin[i]);
while(!s.empty() && s.top() == vout[j])
{
s.pop();
j++;
}
}
if(i == j)
{
cout << "出栈序列合法" << endl;
}
else
{
cout << "出栈序列不合法" << endl;
}
return 0;
}
3.1.1 该题的设计思路
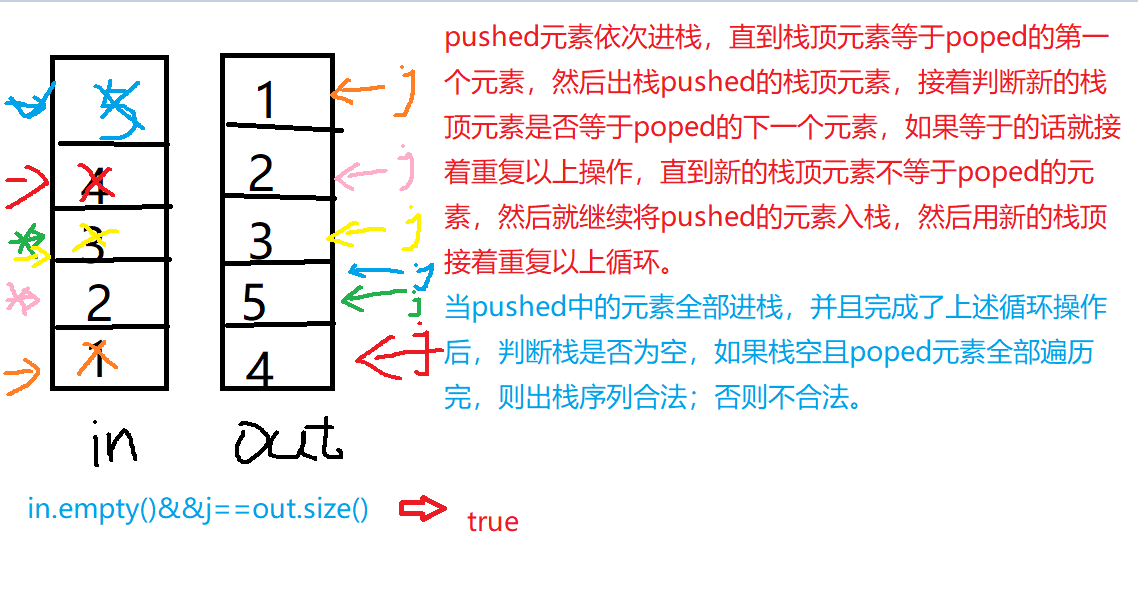
- 时间复杂度:
T(n)=O(n²) - 空间复杂度:
S(n)=O(n)
3.1.2 该题的伪代码
输入元素个数total;
输入入栈顺序instr;
输入出栈顺序outstr;
vector<int> vin,vout;
for(遍历instr) 将instr中的元素入栈到vin中;
for(遍历outstr) 将outstr中的元素入栈到vout中;
int i=j=0;
stack<int> s;
for(i=0 to total-1)
vin[i]入栈到s中;
while(s不为空&&s栈顶元素==vout[j]) s.pop(), j++;
end for
if(i==j) 出栈序列合法;
else 出栈序列不合法;
3.1.3 运行结果
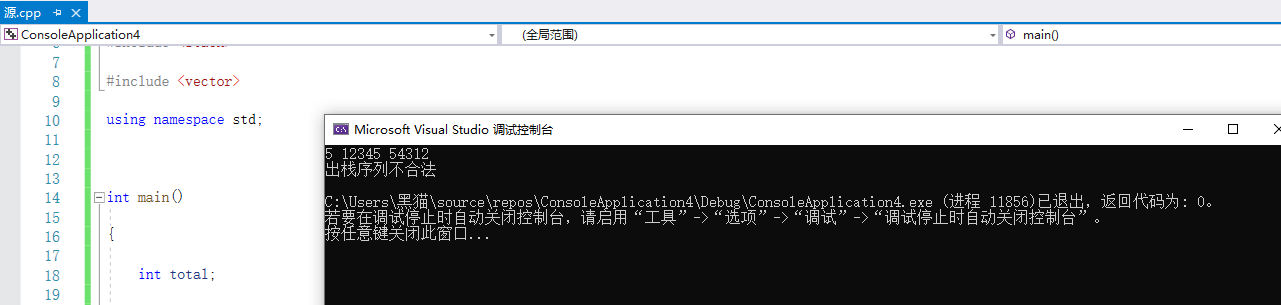

3.1.4分析该题目解题优势及难点。
- 解题优势:可以利用现有的STL容器
stack和vector,操作起来方便快捷,而且不会造成内存浪费;用string类型来存储进栈出栈顺序,方便对其中的任意位置的元素进行操作和使用。 - 难点:在比对出栈顺序时,要注意
pushed栈出栈后,还要接着拿新的栈顶元素来进行比对,不能直接将下一个元素入栈,否则会造成结果出错;要注意在出栈操作之前一定要判断栈是否为空,否则容易引发系统报错!
3.2 题目及解题代码
#include<stdio.h>
#include<stack>
#include<iostream>
#include<string>
using namespace std;
float oper(float f1,float f2, char op)
{
if(op=='+')
return f1+f2;
else if(op=='-')
return f1-f2;
else if(op=='*')
return f1*f2*1.0;
else if(op=='/')
return f1*1.0/f2;
}
int main()
{
stack<float> s;
string prefixExp;
getline(cin,prefixExp);
int strLen=prefixExp.length();
int temp,i,j;
int t1,t2;
for(i=strLen-1;i>=0;i--)
{
string digitStr="";
if(prefixExp[i]=='+' || prefixExp[i]=='-' || prefixExp[i]=='*' || prefixExp[i]=='/') //运算符
{
t1=s.top();
s.pop();
t2=s.top();
s.pop();
if(t2==0 && prefixExp[i]=='/')
{
printf("ERROR\n");
return 0;
}
s.push(oper(t1,t2,prefixExp[i]));
// printf("%f\n",s.top());
i--;//下一位肯定是空格
}
else //运算数
{
while(i>=0 && prefixExp[i]!=' ') //不要漏掉i>=0条件
{
digitStr=prefixExp[i]+digitStr;
i--;
}
//printf("atof:%f\n",atof(digitStr.c_str()));
s.push(atof(digitStr.c_str()));
}
}
if(s.size()==1)
printf("%0.1f\n",s.top());
else
printf("ERROR\n");
return 0;
}
3.2.1 该题的设计思路

- 时间复杂度:T(n)=O(n)
- 空间复杂度:S(n)=O(n)
3.2.2 该题的伪代码
stack<float> s;
输入前缀表达式prefixExp;
for(从后往前遍历前缀表达式)
if(运算符)
里栈顶最近的两个操作数出栈t1,t2;
if(运算符是除号并且除数为0) ERROR!;
将运算结果“t1运算符t2”入栈到s中;
i--;
else //操作数
while(i>=0&&当前字符不是空格)
将当前数字字符转换为整型类型的数字,i--;
end while
将转换成整型的操作数入栈;
end for
if(栈内只剩一个元素) 保留一位小数后输出栈顶元素;
else 表达式有误! 输出ERROR!
3.2.3 运行结果
3.2.4 分析该题目解题优势及难点。
- 解题优势:计算前缀表达式的过程和计算后缀表达式式的过程相反,它是从后向前扫描的。所以可以用
string类型来存储表达式,这样就不会造成内存浪费,操作起来也更加方便。这题同样也可以利用现有的STL容器stack来对栈进行操作,操作起来也很方便,只需要考虑栈空的情况即可。 - 难点:由于输入的表达式中含空格,所以在处理数据的时候需要对空格进行额外的判断,以免误将空格当操作数而入栈;在出栈操作数之前要注意判断栈是否为空,对空栈进行出栈操作会引发系统报错!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号