「学习笔记」线段树合并

「学习笔记」线段树合并

点击查看目录

目录

• 「学习笔记」线段树合并
  • 数据结构
    • 动态开点
    • 权值线段树
    • 线段树合并
  • 例题：魔法少女LJJ
    • 题意
    • 思路
    • 代码
  • 练习题
  • bzoj4919 大根堆和luogu P4577[FJOI2018]领导集团问题
    • 雨天的尾巴
      • 思路
      • 代码
    • P4219 [BJOI2014]大融合
      • 思路
      • 代码
    • [ZJOI2010]基站选址
      • 思路
      • 代码
    • [PKUWC2018]Minimax
      • 思路
      • 代码

数据结构

前置数据结构——普通线段树

动态开点

有的时候线段树节点很多，并不需要一次全部建完整棵树，此时需要动态开点。

由于点是动态开的，所以每个点的字节点不是固定的，需要特意存一下。

权值线段树

权值线段数维护的不再是区间了，而是一堆桶。

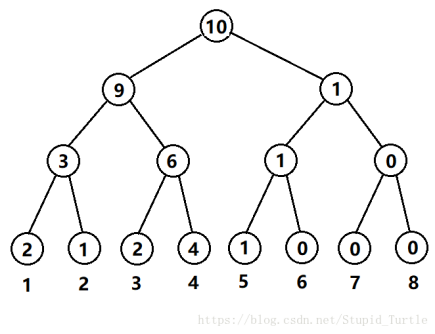
举个例子，我们现在有一个长度为 \(10\) 的数组 1,5,2,3,4,1,3,4,4,4。

\(1\) 出现了 \(2\) 次，\(2\) 出现了 \(1\) 次，\(3\) 出现了 \(2\) 次，\(4\) 出现了 \(4\) 次，\(5\) 出现了 \(1\) 次。

那么这个线段树长这样：

线段树合并

思路就是：

设当前正在合并 \(p1,p2\) 两个节点

如果其中一个为空，则直接返回另一个点的编号。

否则把两个点的值合起来，存到 \(p1\) 的值里。

然后合并它们的左子树和右子树，并把返回的节点编号当做 \(p1\) 的左右儿子。

最后返回 \(p1\)。

比如这两棵线段树：

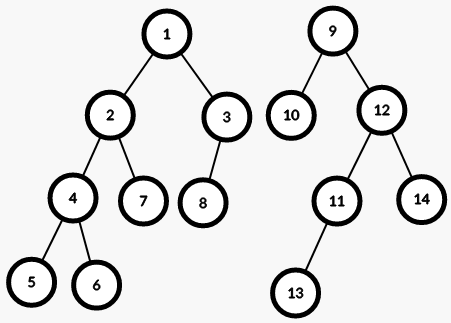
合并完了长这样：

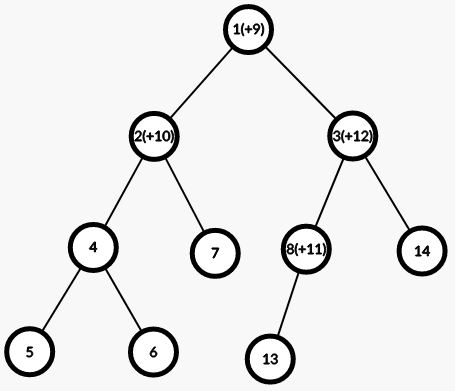
例题：魔法少女LJJ

题意

给你一个动态图，支持以下操作：

1. 新建一个节点，权值为 \(x\) 。
2. 连接两个节点。
3. 将一个节点 \(a\) 所属于的联通块内权值小于 \(x\) 的所有节点权值变成 \(x\) 。
4. 将一个节点 \(a\) 所属于的联通块内权值大于 \(x\) 的所有节点权值变成 \(x\) 。
5. 询问一个节点 \(a\) 所属于的联通块内的第 \(k\) 小的权值是多少。
6. 询问一个节点 \(a\) 所属联通块内所有节点权值之积与另一个节点 \(b\) 所属联通块内所有节点权值之积的大小。
7. 询问 \(a\) 所在联通块内节点的数量
8. 若两个节点 \(a,b\) 直接相连，将这条边断开。
9. 若节点 \(a\) 存在，将这个点删去。

对 \(100\%\) 的数据 \(0\le m\le 4\times 10^5,c\le 7\)，所有出现的数均 \(\le 10^9\)，所有出现的点保证存在。

思路

首先这道题是道诈骗题，因为 \(c\le 7\)，但原题面中还给了两个删点删边的操作（\(8,9\) 操作）。

我们写一个并查集和权值线段树，对于每个操作：

1. 新建一个节点，权值为 \(x\) 。
   新建一棵权值线段树。

2. 连接两个节点。
   把一个点当成另一个点的爹，合并两个权值线段树。

3. 将一个节点 \(a\) 所属于的联通块内权值小于 \(x\) 的所有节点权值变成 \(x\) 。
   分三步走：

   1. 令 \(sum\) 等于当前联通块小于 \(x\) 的节点的数量。
   2. 删除当前联通块小于 \(x\) 的节点。
   3. 在点 \(x\) 上加上 \(sum\)。

4. 将一个节点 \(a\) 所属于的联通块内权值大于 \(x\) 的所有节点权值变成 \(x\) 。
   分三步走：

   1. 令 \(sum\) 等于当前联通块大于 \(x\) 的节点的数量。
   2. 删除当前联通块大于 \(x\) 的节点。
   3. 在点 \(x\) 上加上 \(sum\)。

5. 询问一个节点 \(a\) 所属于的联通块内的第 \(k\) 小的权值是多少。
   如果左子树数的数量比 \(k\) 大，就进入左子树，否则把 \(k\) 减去左子树数的数量再进入右子树。

6. 比较一个节点 \(a\) 所属联通块内所有节点权值之积与另一个节点 \(b\) 所属联通块内所有节点权值之积的大小。

   众所周知，\(\log_2(nm)=\log_2(n)+\log_2(m)\)。

   那么我们根据这个性质，维护并比较每个连同块的对数之和即可。

7. 询问 \(a\) 所在联通块内节点的数量
   直接输出该权值线段树内的节点数量（或者像我一样在并查集里维护）。

代码

点击查看代码

#include<bits/stdc++.h>
#define _for(i,a,b) for(int i=a;i<=b;++i)
#define for_(i,a,b) for(int i=a;i>=b;--i)
using namespace std;
const int N=4e5+1,inf=0x3f3f3f3f;
int q,n,m,a[N][4],num[N],op;
inline int rnt(){
	int x=0,w=1;char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')w=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+(c^48),c=getchar();
	return x*w;
}
namespace LISAN{
	int ls[N];
	void Add(int x){ls[++m]=x;}
	void Lisan(){
		sort(ls+1,ls+m+1);
		m=unique(ls+1,ls+m+1)-ls-1;
	}
	int Find(int x){
		int w=lower_bound(ls+1,ls+m+1,x)-ls;
		return w;
	}
}
namespace XDS{
	int tot=0;
	struct XDS_{
		int lson,rson;
		int val,bj;
		double lg;
	}tr[N*19];
	#define ls(p) tr[p].lson
	#define rs(p) tr[p].rson
	#define va(p) tr[p].val
	#define bj(p) tr[p].bj
	#define lg(p) tr[p].lg
	#define bdmd int mid=(l+r)>>1
	void push_down(int p){
		if(!bj(p))return;
		bj(ls(p))=bj(rs(p))=1;
		lg(ls(p))=lg(rs(p))=0.0;
		va(ls(p))=va(rs(p))=0;
		bj(p)=0;
		return;
	}
	void UpdateP(int &p,int l,int r,int x,int val){
		if(!p)p=++tot;
		if(l>x||r<x)return;
		if(l==r)va(p)+=val,lg(p)+=double(val)*log10(LISAN::ls[l]);
		else{
			bdmd;
			push_down(p);
			UpdateP(ls(p),l,mid,x,val);
			UpdateP(rs(p),mid+1,r,x,val);
			va(p)=va(ls(p))+va(rs(p));
			lg(p)=lg(ls(p))+lg(rs(p));
		}
		return;
	}
	void Delete(int &p,int l,int r,int le,int ri){
		if(!p)return;
		push_down(p);
		if(l>ri||r<le)return;
		if(l>=le&&r<=ri){
			bj(p)=1;
			va(p)=0;
			lg(p)=0.0;
		}
		else{
			bdmd;
			Delete(ls(p),l,mid,le,ri);
			Delete(rs(p),mid+1,r,le,ri);
			va(p)=va(ls(p))+va(rs(p));
			lg(p)=lg(ls(p))+lg(rs(p));
		}
		return;
	}
	int QuerySZ(int p,int l,int r,int le,int ri){
		if(!p)return 0;
		if(l>ri||r<le)return 0;
		push_down(p);
		if(l>=le&&r<=ri)return va(p);
		else{
			bdmd;
			int ans1=QuerySZ(ls(p),l,mid,le,ri);
			int ans2=QuerySZ(rs(p),mid+1,r,le,ri);
			return ans1+ans2;
		}
	}	
	double QueryLG(int p,int l,int r,int le,int ri){
		if(!p)return 0.0;
		if(l>ri||r<le)return 0.0;
		push_down(p);
		if(l>=le&&r<=ri)return lg(p);
		else{
			bdmd;
			double ans1=QueryLG(ls(p),l,mid,le,ri);
			double ans2=QueryLG(rs(p),mid+1,r,le,ri);
			return ans1+ans2;
		}
	}
	int Merge(int p1,int p2){
		if(!p1)return p2;
		if(!p2)return p1;
		push_down(p1);
		push_down(p2);
		va(p1)=va(p1)+va(p2);
		lg(p1)=lg(p1)+lg(p2);
		ls(p1)=Merge(ls(p1),ls(p2));
		rs(p1)=Merge(rs(p1),rs(p2));
		return p1;
	}
	int Kth(int p,int l,int r,int k){
		if(!p)return 0;
		if(l==r)return l;
		else{
			bdmd;
			push_down(p);
			push_down(ls(p));
			push_down(rs(p));
			if(va(ls(p))>=k)
				return Kth(ls(p),l,mid,k);
			else
				return Kth(rs(p),mid+1,r,k-va(ls(p)));
		}
	}
	#undef ls
	#undef rs
	#undef va
	#undef md
}
namespace BCJ{
	int rt[N],fa[N],sz[N];
	int Find(int x){
		if(fa[x]==x)return x;
		return fa[x]=Find(fa[x]);
	}
	void Merge(int x,int y){
		int zx=Find(x),zy=Find(y);
		if(zx==zy)return;
		fa[zy]=zx;
		sz[zx]+=sz[zy];
		XDS::Merge(rt[zx],rt[zy]);
		return;
	}
}
int main(){
	q=rnt();
	_for(i,1,q){
		int op=a[i][1]=rnt();
		if(op==1||op==7)
			a[i][2]=rnt();
		if(op==2||op==3||op==4||op==5||op==6)
			a[i][2]=rnt(),a[i][3]=rnt();
		if(op==1)
			LISAN::Add(a[i][2]);
		if(op==3||op==4)
			LISAN::Add(a[i][3]);
	}
	LISAN::Lisan();
	_for(i,1,q){
		int op=a[i][1],x=a[i][2],y=a[i][3];
		if(op==1){
			x=LISAN::Find(x);
			++n;
			BCJ::fa[n]=n;
			BCJ::sz[n]=1;
			XDS::UpdateP(BCJ::rt[n],1,m,x,1);
		}
		if(op==2){
			BCJ::Merge(x,y);
		}
		if(op==3){
			y=LISAN::Find(y);
			int r=BCJ::rt[BCJ::Find(x)];
			int sum=XDS::QuerySZ(r,1,m,1,y-1);
			XDS::Delete(r,1,m,1,y-1);
			XDS::UpdateP(r,1,m,y,sum);
		}
		if(op==4){
			y=LISAN::Find(y);
			int r=BCJ::rt[BCJ::Find(x)];
			int sum=XDS::QuerySZ(r,1,m,y+1,m);
			XDS::Delete(r,1,m,y+1,m);
			XDS::UpdateP(r,1,m,y,sum);
		}
		if(op==5){
			int r=BCJ::rt[BCJ::Find(x)];
			printf("%intd\n",LISAN::ls[XDS::Kth(r,1,m,y)]);
		}
		if(op==6){
			int rx=BCJ::rt[BCJ::Find(x)];
			int ry=BCJ::rt[BCJ::Find(y)];
			double ax=XDS::QueryLG(rx,1,m,1,m);
			double ay=XDS::QueryLG(ry,1,m,1,m);
			printf("%d\n",(ax>ay));
		}
		if(op==7){
			int zx=BCJ::Find(x);
			printf("%intd\n",BCJ::sz[zx]);
		}
	}
	return 0; 
}

练习题

bzoj4919 大根堆和luogu P4577[FJOI2018]领导集团问题

没有太大区别，就是一个小根堆一个大根堆。

题解在这里

雨天的尾巴

思路

树上差分。

在 \(x\) 到 \(y\) 的路径上发放 \(z\) 时，在 \(x\) 上给 \(z\) 的数量加一，在 \(y\) 上给 \(z\) 的数量加一，在 \(lca(x,y)\) 上给 \(z\) 的数量减一，在 \(father(lca(x,y))\) 上给 \(z\) 的数量减一。

用权值线段树维护即可，每次直接把儿子们的权值线段树给合起来再查询。

代码

点击查看代码

#include<bits/stdc++.h>
#define _for(i,a,b) for(int i=a;i<=b;++i)
#define for_(i,a,b) for(int i=a;i>=b;--i)
#define ll long long
#define bdmd int mid=(l+r)>>1
using namespace std;
const int N=2e5+10,inf=0x3f3f3f3f;
int n,m,mxz,ans[N];
vector<int>son[N];
inline int rnt(){
	int x=0,w=1;char c=getchar();
	while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
	while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
	return x*w;
}
template<class T>class ValSegmentTree{
 public:
 	int tot,root[N],cnt_useless,useless_point[N*40];
	struct TREE{
		int left_son=0,right_son=0;
		T val=0,mx=0;
	}tr[N*100];
	const TREE NONE=(TREE){0,0,0,0};
	// 定义 TREE 类型不存在的量
	#define ls(p) tr[p].left_son
	#define rs(p) tr[p].right_son
	#define va(p) tr[p].val
	#define mx(p) tr[p].mx
	#define mw(p) tr[p].mw
	inline int NewP(){// 新建点
		if(cnt_useless)
			return useless_point[cnt_useless--];
		return ++tot;
	}// 新建点
	inline void DeleteP(int p){// 删除点
		useless_point[++cnt_useless]=p;
		tr[p]=NONE;
		return;
	}// 删除点
	inline void PushUp(int p,int q1,int q2){//向上更新
		va(p)=va(q1)+va(q2);
		mx(p)=max(mx(q1),mx(q2));
		return;
	}//向上更新
	void Update(int &p,int l,int r,int x,int val){// 更新点
		if(!p)p=NewP();
		if(l>x||r<x)return;
		if(l==r)va(p)+=val,mx(p)+=val;
		else{
			bdmd;
			Update(ls(p),l,mid,x,val);
			Update(rs(p),mid+1,r,x,val);
			va(p)=va(ls(p))+va(rs(p));
			mx(p)=max(mx(ls(p)),mx(rs(p)));
		}
		return;
	}// 更新点
	int QueryMax(int p,int l,int r){// 求最多的数
		if(l==r)return mx(p)?l:0;
		else{
			bdmd;
			if(mx(ls(p))>=mx(rs(p)))
				return QueryMax(ls(p),l,mid);
			else
				return QueryMax(rs(p),mid+1,r);
		}
	}// 求最多的数
	void Merge(int &p1,int p2,int l,int r){// 合并
		if(!p1||!p2){p1+=p2;return;}
		bdmd;
		va(p1)+=va(p2);
		Merge(ls(p1),ls(p2),l,mid);
		Merge(rs(p1),rs(p2),mid+1,r);
		if(l==r)mx(p1)=va(p1);
		else mx(p1)=max(mx(ls(p1)),mx(rs(p1)));
		return;
	}// 合并
};
ValSegmentTree<int>tr;
namespace LCA{
	int fa[N],tag[N],rf[N];//rf:Really Father
	struct qu{int y,z;};
	vector<qu> ask[N];
	inline void AddAsk(int x,int y,int z){// 把询问的点对加进来
		ask[x].push_back((qu){y,z});
		if(x!=y)ask[y].push_back((qu){x,z});
		return;
	}// 把询问的点对加进来
	inline void Pre(){// 并查集预处理
		_for(i,1,n)fa[i]=i;
		return;
	}// 并查集预处理
	int Find(int x){// 并查集查找
		if(fa[x]==x)return x;
		return fa[x]=Find(fa[x]);
	}// 并查集查找
	void Tarjan(int u,int father){// Tarjan求LCA
		int sz=son[u].size();
		rf[u]=father;
		_for(i,0,sz-1){
			int v=son[u][i];
			if(v==father)continue;
			Tarjan(v,u);
			fa[v]=u;
		}
		tag[u]=1;
		sz=ask[u].size();
		_for(i,0,sz-1){
			int y=ask[u][i].y,z=ask[u][i].z;
			if(tag[y]){
				int lca=Find(y);
				tr.Update(tr.root[u],1,mxz,z,1);
				tr.Update(tr.root[y],1,mxz,z,1);
				tr.Update(tr.root[lca],1,mxz,z,-1);
				tr.Update(tr.root[rf[lca]],1,mxz,z,-1);
			}
		}
		return;
	}// Tarjan求LCA
}
void SolveAns(int u,int father){// dfs求解
	int sz=son[u].size();
	_for(i,0,sz-1){
		int v=son[u][i];
		if(v==father)continue;
		SolveAns(v,u);
		tr.Merge(tr.root[u],tr.root[v],1,mxz);
	}
	ans[u]=tr.QueryMax(tr.root[u],1,mxz);
	return;
}// dfs求解
int main(){
	n=rnt(),m=rnt();
	LCA::Pre();
	_for(i,2,n){
		int x=rnt(),y=rnt();
		son[x].push_back(y);
		son[y].push_back(x);
	}
	_for(i,1,m){
		int x=rnt(),y=rnt(),z=rnt();
		LCA::AddAsk(x,y,z);
		mxz=max(mxz,z);
	}
	LCA::Tarjan(1,0);
	SolveAns(1,0);
	_for(i,1,n)
		printf("%d\n",ans[i]);
	return 0;
}

P4219 [BJOI2014]大融合

思路

很神奇的一个题。

首先我们与处理出这几棵树的 dfs 序来。

然后让每个节点的线段树里在其 dfs 序的位置加上 \(1\)。

对于加边操作，我们把两个点祖先的权值线段树合起来。

对于查询操作，我们设 \(ans1=\) 深度较大的节点的子树大小，再用当前整棵树的大小减去 \(ans1\) 得 \(ans2\)，就求出了这两个点两边各自的节点数量。

再用 \(ans1\times ans2\)，就可得到答案了。

代码

点击查看代码

#include<bits/stdc++.h>
#define _for(i,a,b) for(ll i=a;i<=b;++i)
#define for_(i,a,b) for(ll i=a;i>=b;--i)
#define ll long long
using namespace std;
const ll N=1e5+10,inf=0x3f3f3f3f;
ll n,q,w[N],m,dfn[N][2];
vector<ll>son[N];
class ValSegmentTree{
 public:
 	ll tot=0,root[N];
 	class TREE{
 	 public:
 		ll left_son;
 		ll right_son;
 		ll val;
 	}tree[N*40];
 	#define ls(p) tree[p].left_son
 	#define rs(p) tree[p].right_son
 	#define va(p) tree[p].val
 	#define l_s(p) ls(p),l,mid
 	#define r_s(p) rs(p),mid+1,r
 	#define bdmd ll mid=(l+r)>>1;
 	void Update(ll &p,ll l,ll r,ll x,ll val){
 		if(!p)p=++tot;
 		if(x<l||r<x)return;
 		if(l==r)va(p)+=val;
 		else{
 			bdmd;
 			Update(l_s(p),x,val);
 			Update(r_s(p),x,val);
 			va(p)=va(ls(p))+va(rs(p));
 		}
 		return;
 	}
 	ll Query(ll p,ll l,ll r,ll le,ll ri){
 		if(ri<l||r<le)return 0;
 		if(le<=l&&r<=ri)return va(p);
 		else{
 			bdmd;
 			return Query(l_s(p),le,ri)+Query(r_s(p),le,ri);
 		}
 	}
 	void Merge(ll &p1,ll p2){
 		if(!p1||!p2){p1+=p2;return;}
 		va(p1)+=va(p2);
 		Merge(ls(p1),ls(p2));
 		Merge(rs(p1),rs(p2));
 		return;
 	}
}tr;
class BCJ{
 public:
 	ll fa[N],sz[N];
 	inline void Pre(){
 		_for(i,1,n)fa[i]=i,sz[i]=1;
 		return;
 	}
 	inline ll Find(ll x){
 		if(fa[x]==x)return x;
 		return fa[x]=Find(fa[x]);
 	}
}bcj;
namespace SOLVE{
	char op[N];
	ll x[N],y[N];
	inline ll rnt(){
		ll x=0,w=1;char c=getchar();
		while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
		while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
		return x*w;
	}
	inline char rch(){
		char c=getchar();
		while(c!='A'&&c!='Q')c=getchar();
		return c;
	}
	void Dfs(ll u,ll father){
		dfn[u][0]=++m;
		tr.Update(tr.root[u],1,2*n,m,1);
		ll sz=son[u].size();
		_for(i,0,sz-1){
			ll v=son[u][i];
			if(v==father)continue;
			Dfs(v,u);
		}
		dfn[u][1]=++m;
		return;
	}
	inline void In(){
		n=rnt(),q=rnt();
		_for(i,1,q){
			op[i]=rch();
			x[i]=rnt(),y[i]=rnt();
			if(op[i]=='A'){
				son[x[i]].push_back(y[i]);
				son[y[i]].push_back(x[i]);
			}
		}
	}
	inline void Pre(){
		_for(i,1,n)
			if(!dfn[i][0])
				SOLVE::Dfs(i,0);
		bcj.Pre();
	}
	inline void Out(){
		_for(i,1,q){
			ll fx=bcj.Find(x[i]);
			ll fy=bcj.Find(y[i]);
			if(op[i]=='A'){
				tr.Merge(tr.root[fx],tr.root[fy]);
				bcj.fa[fy]=fx;
				bcj.sz[fx]+=bcj.sz[fy];
			}
			else{
				ll ans1=tr.Query(tr.root[fx],1,m,dfn[x[i]][0],dfn[x[i]][1]);
				ll ans2=tr.Query(tr.root[fx],1,m,dfn[y[i]][0],dfn[y[i]][1]);
				if(ans1>ans2)swap(ans1,ans2);
				printf("%lld\n",ans1*(bcj.sz[fx]-ans1));
			}
		}
		return;
	}
}
int main(){
	SOLVE::In();
	SOLVE::Pre();
	SOLVE::Out();
	return 0;
}

[ZJOI2010]基站选址

思路

NBdp 题。

首先我们预处理出第 \(i\) 个村庄最左/右的对该村庄产生影响的基站位置 st[i] 和 en[i]，并把该村庄是那些村庄的 en[i] 存进 tmp[i]。

设 \(f_{i,j}\) 表示第 \(i\) 个基站建在村庄 \(j\) 时所需的最小费用（赔偿只算前面的，暂时不算后面的）。

枚举 \(k\) 的个数，然后我们用线段树维护当前的 \(f\) 值。

然后就开始 NB 了。

转移 \(f_{i,j}\) 的时候，我们查询线段树区间 \([1,j-1]\) 的最小值。

然后我们对于每个 tmp[j]，我们在线段树上给区间 \([1,st[tmp[j]]-1]\) 减去 w[j]，因为在 \(j\) 之后没有基站再会影响它，如果选的村庄比 st[tmp[j]] 还小，那么 tmp[j] 必然会被赔偿。

因为我们没有算到后面的赔偿，所以为了防止有的赔偿漏算，我们再 \(new\) 一个免费建基站，不需要赔偿，距离极远，没有任何基站覆盖的到的大公无私的新村庄，即 ++n。

为防止到这个新村庄时没基站了，我们再加上一个基站，即 ++k。

代码

点击查看代码

#include<bits/stdc++.h>
#define _for(i,a,b) for(ll i=a;i<=b;++i)
#define for_(i,a,b) for(ll i=a;i>=b;--i)
#define far(i,vec) for(auto i:vec)
#define lowb(a,r,x) lower_bound(a+1,a+r+1,x)-a
#define uppb(a,r,x) upper_bound(a+1,a+r+1,x)-a
#define bdmd int mid=(l+r)>>1
#define ll long long
using namespace std;
const ll N=2e4+10,inf=0x3f3f3f3f3f;
ll n,k,d[N],c[N],s[N],w[N],f[N],ans;
int st[N],en[N];
vector<int>tmp[N];
class ValSegmentTree{
 public:
	class TREE{
	 public:
		ll tag,minn;
	}tree[N*8];
	#define ls(p) (p<<1)
	#define rs(p) (p<<1|1)
	#define ta(p) tree[p].tag
	#define mn(p) tree[p].minn
	#define l_s(p) ls(p),l,mid
	#define r_s(p) rs(p),mid+1,r
	inline void PushUp(int p){
		mn(p)=min(mn(ls(p)),mn(rs(p)));
		return;
	}
	inline void PushDown(int p){
		if(!ta(p))return;
		ta(ls(p))+=ta(p);
		ta(rs(p))+=ta(p);
		mn(ls(p))+=ta(p);
		mn(rs(p))+=ta(p);
		ta(p)=0;
		return;
	}			
	void Build(int p,int l,int r){
	    ta(p)=0;
		if(l==r)mn(p)=f[l];
		else{
			bdmd;
			Build(ls(p),l,mid);
			Build(rs(p),mid+1,r);
			PushUp(p);
		}
		return;
	}
	void Update(int p,int l,int r,int le,int ri,int val){
		if(ri<l||r<le)return;
		PushDown(p);
		if(le<=l&&r<=ri){
			ta(p)+=val;
			mn(p)+=val; 
		}
		else{
			bdmd;
			Update(l_s(p),le,ri,val);
			Update(r_s(p),le,ri,val);
			PushUp(p);
		}
		return;
	}
	ll Query(int p,int l,int r,int le,int ri){
		if(ri<l||r<le)return inf;
		PushDown(p);
		if(le<=l&&r<=ri)return mn(p);
		else{
			bdmd;
			return min(Query(l_s(p),le,ri),Query(r_s(p),le,ri));
		}
	}
	#undef ls
	#undef rs
	#undef ta
	#undef mn
	#undef l_s
	#undef r_s
}tr;
namespace SOLVE{
	inline ll rnt(){
		ll x=0;char c=getchar();
		while(!isdigit(c))c=getchar();
		while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
		return x;
	}
	inline void In(){
		n=rnt(),k=rnt();
		_for(i,2,n)d[i]=rnt();
		_for(i,1,n)c[i]=rnt();
		_for(i,1,n)s[i]=rnt();
		_for(i,1,n)w[i]=rnt();
	}
	inline void Pre(){
		++n,++k;
		d[n]=w[n]=inf;
		_for(i,1,n){
			st[i]=lowb(d,n,d[i]-s[i]);
			en[i]=uppb(d,n,d[i]+s[i])-1;
			tmp[en[i]].push_back(i);
		}
		ll sum=0;
		_for(i,1,n){
			f[i]=sum+c[i];
			far(j,tmp[i])sum+=w[j];
		}
		ans=f[n];
	}
	inline void Solve(){
		_for(j,2,k){
			tr.Build(1,1,n);
			_for(i,1,n){
				f[i]=(i<j)?inf:(tr.Query(1,1,n,1,i-1)+c[i]);
				far(kk,tmp[i])tr.Update(1,1,n,1,st[kk]-1,w[kk]);
			}
			ans=min(ans,f[n]);
		}
		printf("%lld\n",ans);
	}
}
int main(){
#ifndef ONLINE_JUDGE
	freopen("date.in","r",stdin);
#endif
	SOLVE::In();
	SOLVE::Pre();
	SOLVE::Solve();
	return 0;
}

[PKUWC2018]Minimax

思路

NBdp 题 \(\times 2\)。

每个节点开一个线段树，对于叶子节点，直接在给权值处更新概率为 \(1\)。

非叶子节点直接合并儿子：

• 如果两棵树都没有当前节点，直接跳过。

• 如果两棵树都有当前节点，继续往下，同时传递儿子节点代表的区间的左/右儿子的树的这个区间的前/后缀和。

• 如果两棵树只有一棵有当前节点，直接为它打乘法标记

到根之后 Get 一下 answer 就好了。

然后 \(\frac{1}{10000}\) 这个东西取个膜等于 \(796898467\)，直接乘概率然后取模就可以了。

然后我说这个对你们来说显然的东西是因为我刚开始没发现可以这么干然后写了一个类来封装分数学了半天重载运算符最后悲惨地删掉了。

代码

点击查看代码

#include<bits/stdc++.h>
#define _for(i,a,b) for(ll i=a;i<=b;++i)
#define for_(i,a,b) for(ll i=a;i>=b;--i)
#define far(i,vec) for(auto i:vec)
#define lowb(a,r,x) lower_bound(a+1,a+r+1,x)-a
#define uppb(a,r,x) upper_bound(a+1,a+r+1,x)-a
#define bdmd int mid=(l+r)>>1
#define NO nullptr
typedef long long ll;
using namespace std;
const int N=3e5+10,inf=1<<30,Y=796898467;
const ll P=998244353;
ll n,m,fa[N],p[N],v[N],son[N][3],num_cnt[N];
namespace LISAN{
	ll lsn[N];
	void Add(ll num){lsn[++m]=num;}
	void LiSan(){
		sort(lsn+1,lsn+m+1);
		m=unique(lsn+1,lsn+m+1)-lsn-1;
		return;
	}
	ll Q(ll num){return lowb(lsn,m,num);}
};
using LISAN::lsn;
using LISAN::Q;
class ValSegmentTree{
 public:
	int tot=0,root[N];
	class TREE{
	 public:
	 	int left_son,right_son;
	 	ll val,tag=1;
	}tree[N*50];
	#define _(p) p,l,r
	#define ls(p) tree[p].left_son
	#define rs(p) tree[p].right_son
	#define va(p) tree[p].val
	#define ta(p) tree[p].tag
	#define l_s(p) tree[p].left_son,l,mid
	#define r_s(p) tree[p].right_son,mid+1,r
	inline void PushUp(int p){
		va(p)=(va(ls(p))+va(rs(p)))%P;
		return;
	}
	inline void Tag(int p,ll tag){
		if(!tag)return;
		va(p)=va(p)*tag%P;
		ta(p)=ta(p)*tag%P;
		return;
	}
	inline void PushDown(int p){
		if(ta(p)<=1)return;
		ta(ls(p))=(ta(ls(p))*ta(p))%P;
		ta(rs(p))=(ta(rs(p))*ta(p))%P;
		va(ls(p))=(va(ls(p))*ta(p))%P;
		va(rs(p))=(va(rs(p))*ta(p))%P;
		ta(p)=1;
		return;
	}
	void UpdateP(int &p,int l,int r,int x){
		if(r<x||x<l)return;
		if(!p)p=++tot;
		PushDown(p);
		if(l==r)va(p)=1;
		else{
			bdmd;
			UpdateP(l_s(p),x);
			UpdateP(r_s(p),x);
			PushUp(p);
		}
		return;
	}
	void Merge(int &q1,int q2,int l,int r,ll gl1,ll gl2,ll pp){
		if(!q1&&!q2)return;
		if(!q2)
			Tag(q1,gl1);
		else if(!q1){
			q1=q2;
			Tag(q1,gl2);
		}
		else{
			PushDown(q1),PushDown(q2);
			bdmd;
			ll lq1=va(ls(q1)),lq2=va(ls(q2)),rq1=va(rs(q1)),rq2=va(rs(q2));
			Merge(ls(q1),ls(q2),l,mid,
				(gl1+rq2*(1-pp+P)%P)%P,
				(gl2+rq1*(1-pp+P)%P)%P,pp);
			Merge(rs(q1),rs(q2),mid+1,r,
				(gl1+lq2*pp%P)%P,
				(gl2+lq1*pp%P)%P,pp);
			PushUp(q1);
		}
		return;
	}
	ll GetAnswer(int p,int l,int r){
		PushDown(p);
		if(l==r)
			return va(p)*va(p)%P*l%P*lsn[l]%P;
		else{
			bdmd;
			return (GetAnswer(l_s(p))+GetAnswer(r_s(p)))%P;
		}
	}
}tr;
namespace SOLVE{
	inline ll rnt(){
		ll x=0,w=1;char c=getchar();
		while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
		while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
		return x*w;
	}
	void Dfs(int u){
		if(!son[u][0]){
			tr.UpdateP(tr.root[u],1,m,Q(v[u]));
		}
		else{
			Dfs(son[u][1]);
			tr.root[u]=tr.root[son[u][1]];
			if(son[u][0]==2){
				Dfs(son[u][2]);
				tr.Merge(tr.root[son[u][1]],tr.root[son[u][2]],1,m,0,0,p[u]);
			}
		}
	}
	inline void In(){
		n=rnt();
		_for(i,1,n){
			fa[i]=rnt();
			son[fa[i]][++son[fa[i]][0]]=i;
		}
		_for(i,1,n){
			ll x=rnt();
			if(!son[i][1])LISAN::Add(v[i]=x);
			else p[i]=x*Y%P;
		}
	}
	inline void Solve(){
		LISAN::LiSan();
		Dfs(1);
		printf("%lld\n",tr.GetAnswer(tr.root[1],1,m));
	}
}
int main(){
#ifndef ONLINE_JUDGE
	freopen("date.in","r",stdin);
#endif
	SOLVE::In();
	SOLVE::Solve();
	return 0;
}/*
5
0 1 1 2 2
5000 5000 1 2 3

*/

\[\Huge{\mathfrak{The\ End}} \]