「学习笔记」树状数组
树状数组
Question
用一个数据结构维护一个序列,支持单点修改和区间求和。
DataStructure:树状数组
前置知识:lowbit
用来计算一个数二进制下的最低位的1和后面的0构成的数。计算方法为:\(\text{lowbit}(x)=x\&(-x)\)
例如 \(\text{lowbit}(14)=2\):
1 1 1 0---- 14
& 0 0 1 0---- -14
------------------
= 0 0 1 0---- 2
正文:
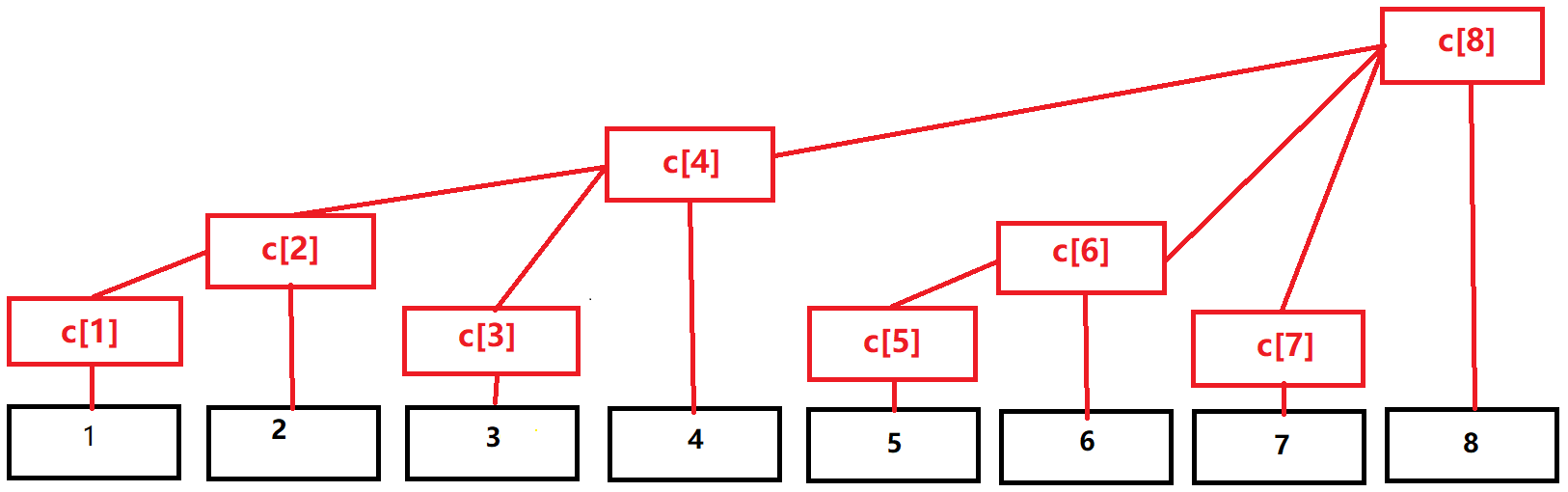
观察这个树状数组,可以得到:
再观察这个树状数组,可以发现:
-
树状数组中某个节点 \(i\) 的父节点的下标为 \(i+\text{lowbit(i)}\) 。
例如 \(c_1\) 他爹为 \(c_{1+1\&(-1)}=c_2\) ,\(c_2\) 他爹为 \(c_{2+2\&(-2)}=c_4\) ,\(c_4\) 他爹为 \(c_{4+4\&(-4)}=c_8\) 。
由此可知单点修改的方法为:沿着父节点一路向上爬,直到更新完整个区间。
复杂度为 \(O(n*lg(n))\)。
-
树状数组中某个节点 \(i\) 的左兄弟下标为 \(i-\text{lowbit(i)}\)
例如 \(c_7\) 左兄弟为 \(c_{7-7\&(-7)}=c_3\),\(c_3\) 左兄弟为 \(c_{3-3\&(-3)}=c_1\)
由此可知查询前缀和的方法为:从最右边的端点开始一直爬左兄弟进行累计。
复杂度为 \(O(n*lg(n))\)。
Code
lowbit:
ll lowbit(int x){return x&(-x);}
修改:
void update(int x,int y){
while(x<=n){
c[x]+=y;
x+=lowbit(x);
}
}
查询:
ll query(ll x){
ll sum=0;
while(x){
sum+=c[x];
x-=lowbit(x);
}
return sum;
}
易错点:
- 调用函数时参数 \(x\) 不能为非正数,否则
lowbit的值会不动甚至比 \(0\) 还小(例如update(0,1)会死循环)。
Examples
A.Luogu P3368/Loj P131
Meaning of the problem
维护一个序列,进行下面两种操作:
- 将某区间每一个数加上 \(x\) 。
- 求出某一个数的值。
Solution
这道题看似和正常树状数组差不多,但是实际上差距很大。裸的树状数组只能单点修改,所以我们要把区间修改转化为单点修改。那我们应该如何去转换呢?
用树状数组维护差分。
举个例子:
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 原数列 | 1 | 3 | 4 | 2 | 5 | 6 |
| 差分(\(c\)) | 1 | 2 | 1 | -2 | 3 | 1 |
我们在 \((1,4)\) 这个区间加上 \(2\) ,得到:
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 现数列 | 3 | 5 | 6 | 4 | 5 | 6 |
| 差分(\(c\)) | 3 | 2 | 1 | -2 | 1 | 1 |
| 差分变化 | +2 | 0 | 0 | 0 | -2 | 0 |
可以发现:差分中只有 \(1\) 处增加了 \(2\) , \(4+1=5\) 处减去了 \(2\) !
所以我们可以得出一个结论:
对区间 \((l,r)\) 的每一个数加上 \(v\) ,会得到 \(c_l=c_l+v,c_{r+1}=c_{r+1}-v\)。
那么我们就可以用树状数组去维护差分变化。而且我们还可以发现一个区间加值在差分的前缀和中,产生的影响仅是该区间的差分前缀和中加上该值。所以单点查询的方法为:用原数组的值加上差分的前缀和。
Code
const int N=1e5+10;
ll n,q,a[N],c[N];
ll lowbit(ll x){return x&(-x);}
void update(ll x,ll y){while(x<=n)c[x]+=y,x+=lowbit(x);}
ll query(ll x){
ll sum=0;
while(x)sum+=c[x],x-=lowbit(x);
return sum;
}
int main(){
n=read();
_for(i,1,n)a[i]=read();
q=read();
while(q--){
op=read();
if(op==1){
ll l=read(),r=read(),d=read();
update(l,d),update(r+1,-d);
}else{
ll d=read();
printf("%lld\n",a[d]+query(d));
}
}
return 0;
}
B.Loj P10114
Meaning of the problem
给定 \(n\) 点,定义每个点的等级是在该点左下方(含正左、正下)的点的数目,试统计每个等级有多少个点。
星星按 \(y\) 坐标增序给出,\(y\) 坐标相同的按 \(x\) 坐标增序给出。
对于全部数据,\(1\le N \le 1.5*10^4,0\le x,y \le 3.2*10^5\) 。
Solution
乍一看:二维树状数组。
仔细一看:数组开不下。
再仔细一看:题目排好序了。
那么我们可以确定,对于第 \(i\) 个点,前面的点都在此点下面,所以我们只要看前面的哪些点在此点左边(即 前面的点的 \(x\) 坐标小于此点的),就知道它左下有多少个点了。
直接用树状数组维护 \(x\) 并动态查询即可。
*有一个点需要注意: \(x,y\) 可能为 \(0\) ,如果不加处理会陷入死循环。我们可以把 \(x\) 整体往后移一位,避免 \(0\) 的出现。
Code
const int N=32010;
int n,a,c[N],ji[N];
inline int lowbit(int x){return x&-x;}
inline void update(int x,int z){while(x<=32010)c[x]+=z,x+=lowbit(x);}
inline int query(int x){
int sum=0;
while(x)sum+=c[x],x-=lowbit(x);
return sum;
}int main(){
n=read();
_for(i,1,n){
a=read();read();
++ji[query(a+1)],update(a+1,1);
}_for(i,0,n-1)printf("%d\n",ji[i]);
return 0;
}
C.Loj P10115
Meaning of the problem
有两个操作:
- 在 \(l,r\) 之间中上一类树。
- 查询 \(l,r\) 之间有几类树。
Solution
把每次种树看成一条线段,然后我们要维护两个东西:\(i\) 左边左端点的数量和右端点的数量。
左端点的数量说明用多少个区间开了,右端点的数量说明又有多少个区间闭合了。
例如:
1 2 3 4 5
1 |---|
2 |---|
3 |-------|
4 |-|
查询 \(3,4\):
\(4\) 左边开了 \(4\) 个区间,\(3\) 左边闭合了 \(1\) 个区间,所以一共有 \(4-1=3\) 种树。
Code
const int N=5e4+10;
int n,m,op,l,r,a[N],c[2][N],ans;
inline int lowbit(int x){return x&-x;}
inline void update(int k,int x,int y){while(x<=n)c[k][x]+=y,x+=lowbit(x);}
inline int query(int k,int x){
int sum=0;
while(x)sum+=c[k][x],x-=lowbit(x);
return sum;
}
int main(){
n=read(),m=read();
while(m--){
op=read(),l=read(),r=read();
if(op==1)update(0,l,1),update(1,r,1);
else printf("%d\n",query(0,r)-query(1,l-1));
}
return 0;
}
D.区间异或和
Meaning of the Problem

Solution
异或和运算有两个性质:
a^b^b=aa^0=a
我们运用这两个性质就可以把它转化成裸的树状数组了。(具体操作见代码)
Code
ll n,m,a[N],op,l,r,c[N],ans;
inline ll lowbit(ll x){return x&-x;}
inline void update1(ll x,ll y){while(x<=n)c[x]^=y,x+=lowbit(x);}
inline void update2(ll x,ll y){
ll z=x;
while(x<=n)c[x]^=a[z]^y,x+=lowbit(x);
}inline ll query(ll x){
ll xor_sum=0;
while(x)xor_sum^=c[x],x-=lowbit(x);
return xor_sum;
}
int main(){
scanf("%lld%lld",&n,&m);
_for(i,1,n)scanf("%lld",&a[i]),update1(i,a[i]);
_for(i,1,m){
scanf("%lld%lld%lld",&op,&l,&r);
if(op)printf("%lld\n",query(r)^query(l-1));
else update2(l,r),a[l]=r;
}
return 0;
}
E.移动电话
Meaning of the Problem

Solution
这道题就是二维树状数组的模板题。
其实二维树状数组和普通的树状数组性质上只是多了一维,即:
- 树状数组中某个节点 \(i,j\) 的父节点的下标为 \(i+\text{lowbit(i)},j+\text{lowbit(j)}\) 。
- 树状数组中某个节点 \(i,j\) 的左兄弟的下标为 \(i-\text{lowbit(i)},j-\text{lowbit(j)}\)
我们直接利用这个性质去写增加一维的树状数组就行了。
注:查询矩阵和的方法:
Code
ll op,n,c[N][N];
ll lowbit(ll x){return x&(-x);}
void update(ll x,ll y,ll z){
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=n;j+=lowbit(j))
c[i][j]+=z;
}ll query(const ll x,const ll y){
ll sum=0;
for(int i=x;i>0;i-=lowbit(i))
for(int j=y;j>0;j-=lowbit(j))
sum+=c[i][j];
return sum;
}int main(){
while(1){
op=read();
if(op==3)break;
else if(op==0)n=read();
else if(op==1){
ll x=read(),y=read(),a=read();
update(x+1,y+1,a);
}else{
ll l=read(),b=read(),r=read(),t=read();
printf("%lld\n",query(r+1,t+1)-query(r+1,b)-query(l,t+1)+query(l,b));
}
}
return 0;
}
G.求逆序对个数
Meaning of the Problem
逆序对的定义:
有一个数列 \(a_1,a_2,a_3,...,a_n\) ,若 \(i<j\) 且 \(a_i>a_j\) ,则称 \(a_i\) 与 \(a_j\) 构成了一个逆序对。
给定数列 \(a\) ,求其中逆序对的个数。
Solution
观察逆序对的性质,可以发现 \(a_i\) 后面比它小的数和它构成了逆序对。
我们可以从最后开始遍历,用树状数组维护 \(a_i\) 后面(比它先遍历)比他小的数的个数,这个个数就是它与后面的数构成的逆序对数
Code
inline int lowbit(int x){return x&-x;}
inline void update(int x,int z){while(x<=N)c[x]+=z,x+=lowbit(x);}
inline int query(int x){
int sum=0;
while(x)sum+=c[x],x-=lowbit(x);
return sum;
}int main(){
scanf("%d",&n);
_for(i,1,n)scanf("%d",&a[i]);
for_(i,n,1)ans+=query(a[i]-1),update(a[i],1);
printf("%d\n",ans);
return 0;
}
Reference
《算法竞赛进阶指南》——李煜东
学校课件


