Welcome To Ke_schol|
收藏闪存小组博问

Ke_scholar

园龄：2年2个月粉丝：30关注：10

2024 暑假友谊赛 2

2024 暑假友谊赛 2

A - 🐕

CodeForces - 1150B

题意

给你 \(n\times n\) 的只包含.和#的矩阵，问你.的部分能否用十的结构补满。

思路

暴力模拟即可。

代码

#include<bits/stdc++.h>
 
using namespace std;
 
using i64 = long long;
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
 
    int n;
    cin >> n;
 
    vector<string> s(n);
    for (auto &i : s) cin >> i;
 
    const int u[] = {1, -1, 0, 0}, v[] = {0, 0, 1, -1};
 
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j ++) {
            if (s[i][j] == '.') {
                int f = 0;
                for (int k = 0; k < 4; k ++) {
                    int x = i + u[k];
                    int y = j + v[k];
                    if (x >= 0 && x < n && y >= 0 && y < n && s[x][y] == '.') {
                        f ++;
                    }
                }
                if (f == 4) {
                    s[i][j] = '#';
                    for (int k = 0; k < 4; k ++) {
                        int x = i + u[k];
                        int y = j + v[k];
                        s[x][y] = '#';
                    }
                }
            }
        }
    }
 
    for (int i = 0; i < n; i ++)
        for (int j = 0; j < n; j ++)
            if (s[i][j] == '.') {
                cout << "No\n";
                return 0;
            }
 
    cout << "Yes\n";
 
    return 0;
}

B - 🐕🐕

CodeForces - 1332D

题意

你需要构造一个矩阵，使得图中存在一条路径，设路径上的值相与得 x，现它有个算法按照 \(dp_{i,j}=\max(dp_{i-1,j}\&a_{i,j},dp_{i,j-1}\&a_{i,j})\) 的转移得到一个 \(dp_{n,m}\) 的值 y, 问你怎样构造矩阵使得 \(x-y=k\)。

思路

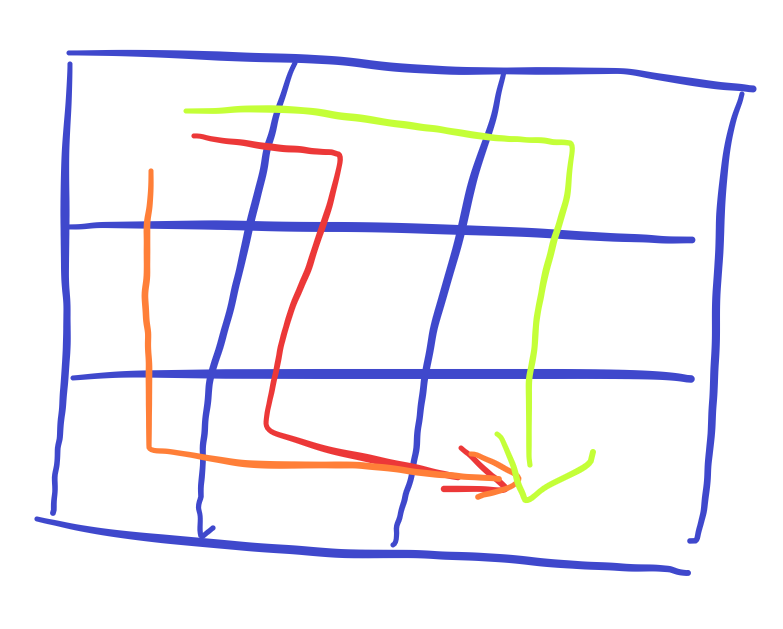
image

观察第二个样例可以得到，我们需要构造使得转移计算的值橙色线最大，绿色线最小，最好使得他们两值与上 \(a_{n,m}\) 都为 0 ，这样我们构造的红色线只要为 k 即可，考虑与值是把两数二进制为 1 的才能为 1，而 \(a_{0,1}\)，和 \(a_{2,1}\) 红色线与其他线重合，需要保持不变，那么绿色线只要全为 0 不用管即可，红色线全为 k，橙色线改变 \(a_{1,0}\)， 假设 \(a_{n,m}\) 为 k，那么为了确保橙色线的最大值与上它后也为 0 ，要让这个最大值 k 位二进制全为 0 即可，即将 1 左移 k 位即可。

注：262143为大于1e5二进制位数的全1二进制数。

代码

#include<bits/stdc++.h>
 
using namespace std;
 
using i64 = long long;
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
 
    int n;
    cin >> n;
 
    int a[3][3] {};
 
    a[2][0] = a[2][1] = a[0][0] = 262143;
    a[0][1] = a[1][1] = a[2][2] = n;
 
    cout << "3 3\n";
 
    int len = log2(n) + 1;
    a[1][0] = (1 << len);
 
    for (int i = 0; i < 3; i ++)
        for (int j = 0; j < 3; j ++)
            cout << a[i][j] << " \n"[j == 2];
 
    return 0;
}

C - 🐕🐕🐕

CodeForces - 1503B

题意

本题是交互题。

Alice 和 Bob 在玩一个游戏：

初始有一个 \(n\times n\) 网格，我们用 \((i,j)\) 表示这个网格第 \(i\) 行第 \(j\) 列的位置，同时初始还有无限个颜色为 \(1,2,3\) 的三种代币。

接下来游戏会进行若干轮，每一轮 Alice 会选择一个颜色 \(a\)，之后 Bob 需要选择一个颜色不是 \(a\) 的代币，并选择网格上一个没有放过代币的位置放上这个代币。

如果当完成一轮之后，有两个相邻的位置上放有相同颜色的代币，则 Alice 获胜。如果 \(n^2\) 轮之后 Alice 仍然没有获胜，则 Bob 获胜。

我们可以证明 Bob 有必胜策略，现在你需要扮演 Bob 并赢下游戏。

交互格式

首先交互器会给你一个整数 \(n\) 表示网格大小。接下来对于每一轮，你需要读入一个整数 \(a\) 表示你这一轮不可以选择什么颜色的代币，然后输出三个整数 \(b,i,j\) 表示你要在 \((i,j)\) 放上颜色为 \(b\) 的代币，\((i,j)\) 必须没有被放过代币。

如果你的操作不合法或是输掉了游戏，交互器会结束输入而你会得到 Wrong answer 的结果，如果 \(n^2\) 轮之后你还没有输掉游戏，请立即结束程序并得到 Accepted 的结果。

思路

考虑 n = 3 ，只填 1 或 2 ，那么当 1 和 2交叉填的时候只能以下这样：

1 2 1
2 1 2
1 2 1

那么上题同理，当我们把 1 的个数或者 2 的个数其中之一这样交叉填满一半的时候，那么剩下的格子都是全部隔开的，只要不填铺满的那个数即可。

代码

#include<bits/stdc++.h>
 
using namespace std;
 
using i64 = long long;
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
 
    int n;
    cin >> n;
 
    int one = 0, two = 0;
    vector a(n + 1, vector<int>(n + 1));
 
    auto solve = [&](int no)->tuple<int, int, int> {
        for (int i = 1; i <= n; i ++) {
            for (int j = 1; j <= n; j ++) {
                if (a[i][j])continue;
                if (one != (n * n + 1) / 2 && two != n * n / 2) {
                    if ((i + j) % 2 == 0 && no != 1) {
                        a[i][j] = 1;
                        one ++;
                        return {1, i, j};
                    }
                    if (((i + j) & 1) && no != 2) {
                        a[i][j] = 2;
                        two ++;
                        return {2, i, j};
                    }
                } else {
                    if (one == (n * n + 1) / 2) {
                        int t = no == 1 ? 2 : (2 ^ 3 ^ no);
                        a[i][j] = t;
                        return {t, i, j};
                    } else {
                        int t = no == 2 ? 1 : (1 ^ 3 ^ no);
                        a[i][j] = t;
                        return {t, i, j};
                    }
                }
            }
        }
    };
 
    for (int i = 1, no; i <= n * n; i ++) {
        cin >> no;
        auto [t, x, y] = solve(no);
        cout << t << ' ' << x << ' ' << y << endl;
    }
 
    return 0;
}

D - 🐕🐕🐕🐕

AtCoder - arc134_b

题意

给定长度为 \(N\) 的字符串 \(s\)。规定 \(s_i\) 表示 \(s\) 的第 \(i\) 个字符。

Snuke 将按下列步骤变换字符串 \(s\) 。

  • 选择\((1,2, \ldots, N)\)中的一个长度为偶数的子序列\(x\)（不一定连续）\(=(x_1, x_2, …, x_{2k})\)。\(k\)可以是\(0\)。
  • 交换\(s_{x_1}\)和\(s_{x_{2k}}\)。
  • 交换\(s_{x_2}\)和\(s_{x_{2k-1}}\)。
  • 交换\(s_{x_3}\)和\(s_{x_{2k-2}}\)。
  • \(\vdots\)
  • 调换\(s_{x_{k}}\)和\(s_{x_{k+1}}\)。

找出经过变换的字符串中，字典序最小的那个。

思路

考虑贪心。

首先我们将每个字母的位置存下来，然后确定一个右边界，枚举左端点，从a到当前字母找有没有字母的位置的比右边界更小，小的话说明有位置可以替换掉当前字母，于是交换一下即可，更新右边界。

代码

#include<bits/stdc++.h>
 
using namespace std;
 
using i64 = long long;
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
 
    int n;
    cin >> n;
 
    string s;
    cin >> s;
 
    map<char, vector<int>> mp;
    for (int i = 0; i < n; i ++) {
        mp[s[i]].push_back(i);
    }
 
    int r = n - 1;
    for (int l = 0; l < n; l ++) {
        for (char c = 'a'; c < s[l] && c < 'z'; c ++) {
            while (mp[c].size() && mp[c].back() > r)
                mp[c].pop_back();
            if (mp[c].size() && mp[c].back() > l) {
                swap(s[l], s[mp[c].back()]);
                r = mp[c].back();
                mp[c].pop_back();
                break;
            }
        }
    }
 
    cout << s << '\n';
 
    return 0;
}

E - 🐕🐕🐕🐕🐕

AtCoder - abc278_d

题意

给定长度为 \(n\) 的数组 \(a\)，每次有三种操作：

  • \(op_i = 1\)，表示将 \(a\) 数组全部元素替换成 \(k\)。
  • \(op_i = 2\)，表示 \(a_i \gets a_i + k\)。
  • \(op_i = 3\)，表示查询 \(a_i\) 的值。

对于每个 \(op_i = 3\)，输出结果。

思路

线段树区间维护操作 1，单点修改维护操作 2 即可。

代码

#include<bits/stdc++.h>
 
using namespace std;
 
using i64 = long long;
 
#define lc u<<1
#define rc u<<1|1
const int N = 2e5 + 5;
i64 w[N], n, m, p;
struct Tree { //线段树
    i64 l, r, sum, add;
} tr[N * 4];
 
void cal_lazy(i64 fa, i64 ch) {
    i64 b = tr[fa].add;
    i64 len = tr[ch].r - tr[ch].l + 1;
    tr[ch].sum = len * b;
}
 
void tag_union(i64 fa, i64 ch) {
    i64 b = tr[fa].add;
    tr[ch].add = b;
}
 
void init_lazy(i64 u) {
    tr[u].add = 0;
}
 
void pushdown(i64 u) {
    if (tr[u].add != 0) {
        cal_lazy(u, lc);
        cal_lazy(u, rc);
        tag_union(u, lc);
        tag_union(u, rc);
        init_lazy(u);
    }
}
 
void pushup(i64 u) { //上传
    tr[u].sum = (tr[lc].sum + tr[rc].sum);
}
 
void build(i64 u, i64 l, i64 r) { //建树
    tr[u].l = l, tr[u].r = r;
    init_lazy(u);
    if (l == r) {
        tr[u].sum = w[l];
        return ;
    }
    i64 mid = (l + r) >> 1;
    build(lc, l, mid);
    build(rc, mid + 1, r);
    pushup(u);
 
}
 
void modify(i64 u, i64 l, i64 r, i64 k) {
    if (tr[u].l >= l && tr[u].r <= r) {
        i64 len = tr[u].r - tr[u].l + 1;
        tr[u].sum = k * len ;
        tr[u].add = k;
        return ;
    }
    pushdown(u);
    i64 mid = (tr[u].l + tr[u].r) >> 1;
    if (l <= mid)
        modify(lc, l, r, k);
    if (r > mid)
        modify(rc, l, r, k);
    pushup(u);
}
 
void modify(i64 u, i64 pos, i64 k) {
    if (tr[u].l == tr[u].r ) {
        tr[u].sum += k;
        return ;
    }
    pushdown(u);
    i64 mid = (tr[u].l + tr[u].r) >> 1;
    if (pos <= mid)
        modify(lc, pos, k);
    else
        modify(rc, pos, k);
    pushup(u);
}
 
i64 query(i64 u, i64 l, i64 r) { //区查
    if (l <= tr[u].l && tr[u].r <= r)
        return tr[u].sum;
    i64 mid = tr[u].l + tr[u].r >> 1;
    pushdown(u);
    i64 res = 0;
    if (l <= mid) res += query(lc, l, r);
    if (r > mid) res += query(rc, l, r);
    return res ;
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
 
    cin >> n;
 
    for (int i = 1; i <= n; i ++)
        cin >> w[i];
 
    build(1, 1, n);
 
    int q;
    cin >> q;
    while (q--) {
        int op, i, x;
        cin >> op;
        if (op == 1) {
            cin >> x;
            modify(1, 1, n, x);
        } else if (op == 2) {
            cin >> i >> x;
            modify(1, i, x);
        } else {
            cin >> i;
            cout << query(1, i, i) << '\n';
        }
    }
 
 
    return 0;
}

F - 🐕🐕🐕🐕🐕🐕

AtCoder - abc216_f

题意

给出两个有 \(n\) 个元素的序列 \(a,b\)，现在在 \(1 - n\) 中选一些数构成集合 \(S\)，使得 \(max_{i \in S} \space a_i \ge \sum_{i \in S} \space b_i\)，问合法的集合 \(S\) 的个数 \(\mod 998244353\)。

思路

考虑 dp。

设 \(dp_i\) 为 b 序列能够凑成的数。

选择一些数，那么将 a 从小到大排序，b 跟着 a 排序得到的答案也是不会变的。

对于第 i 个数，选择它的话，那么其产生的方案数就是 \(\sum_{j-b_i}^{a_i}dp_j\)，这个数对之后的数也会产生贡献，所以要更新后面新的方案数，即对该数进行一次背包。

代码

#include<bits/stdc++.h>
 
using namespace std;
 
using i64 = long long;
 
const int N = 5010, mod = 998244353;
i64 dp[N];
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
 
    int n;
    cin >> n;
 
    vector<array<int, 2>> a(n + 1);
    for (int i = 1; i <= n; i ++)
        cin >> a[i][0];
    for (int i = 1; i <= n; i ++)
        cin >> a[i][1];
 
    sort(a.begin() + 1, a.end());
 
    i64 ans = 0;
 
    dp[0] = 1;
    for (int i = 1; i <= n; i ++) {
        for (int j = a[i][1]; j <= a[i][0]; j ++)
            ans = (ans + dp[j - a[i][1]]) % mod;
        for (int j = 5000; j >= a[i][1]; j--)
            dp[j] = (dp[j] + dp[j - a[i][1]]) % mod;
    }
 
    cout << ans << '\n';
 
    return 0;
}

G - 🐕🐕🐕🐕🐕🐕🐕

CodeForces - 1012B

题意

给你一个 \(n\times m\) 的矩形，一开始有 q 个格子上被标记。对于任意两行两列，如果交汇的四个格子中有三个被标记，那么第 4 个会被自动标记。问你至少需要手动标记几个格子，使得整个矩形内的格子都被标记。

思路

将 n 行 m 列看成 n + m 个点，将 \((x,y),(x+a,y),(x,y+b)\) 被标记的点看成 \(x\rightarrow y，x+a\rightarrow y,x\rightarrow y+b\) 三条边，那么根据题意 \(x+a\rightarrow y+b\) 也会自动连一条边，以此类推形成一整个连通块，那么题目要求完全标记所有元素就转化成了添加多少边可以使得所有的点连通，自然答案就是连通块的数量减 1 了，用并查集计算出连通块的数量即可。

代码

#include <bits/stdc++.h>
 
using namespace std;
 
using i64 = long long;
 
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
 
	int n, m, q;
	cin >> n >> m >> q;
 
	vector<int> fa(n + m + 1);
	iota(fa.begin(), fa.end(), 0);
 
	auto find = [&](auto & f, int x) ->int{
		return fa[x] == x ? x : fa[x] = f(f, fa[x]);
	};
 
	for (int i = 0; i < q; i ++) {
		int x, y;
		cin >> x >> y;
 
		x = find(find, x), y = find(find, y + n);
		if (x != y) {
			fa[x] = y;
		}
	}
 
	int ans = 0 ;
	for (int i = 1; i <= n + m; i++)
		ans += (find(find, i) == i);
 
	cout << ans - 1 << '\n';
 
	return 0;
}

H - 🐕🐕🐕🐕🐕🐕🐕🐕

CodeForces - 1328E

题意

给你一个以 \(1\) 为根的有根树。

每回询问 \(k\) 个节点 \({v_1, v_2 \cdots v_k}\) 。

求出是否有一条以根节点为一端的链使得询问的每个节点到此链的距离均 \(\leq 1\)。

只需输出可行性, 无需输出方案。

思路

每个节点到此链的距离 ≤ 1，说明要么它们的父亲节点在这条链上，要么他们自己在这条链上。又因为这是一棵树，从上到下要到达某个点的话，就必须得经过它的父亲节点，所以那些本身在链上的点，其父亲节点也在这条链上。

那么这题就变成了，给你一些点，判断是否有一条路径经过了这些点的父亲，对这些父亲节点按照他们的深度排序后，观察发现，如果存在这样一条路径的话，那么每一个点都在它前一个点的子树里，因为如果不在前一个点的子树的话，那么说明这个点与前一个点不同子树内，不会存在一条路径经过这两个点。

用 dfs 处理出时间戳，深度，每个点父亲，然后将 k 个点换成其父亲按照深度排序后，判断每个点是否在上一个点的子树内即可。

代码

#include <bits/stdc++.h>
 
using namespace std;
 
using i64 = long long;
 
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
 
	int n, m;
	cin >> n >> m;
 
	vector g(n + 1, vector<int>());
 
	for (int i = 1; i < n; i ++) {
		int u, v;
		cin >> u >> v;
		g[u].push_back(v);
		g[v].push_back(u);
	}
 
	int time = 0;
	vector<int> dfn(n + 1), fa(n + 1), siz(n + 1), dep(n + 1);
	auto dfs = [&](auto & self, int u, int f)->void{
		dfn[u] = ++ time;
		dep[u] = dep[f] + 1, fa[u] = f, siz[u] = 1;;
		for (auto v : g[u]) {
			if (v == f) continue;
			self(self, v, u);
			siz[u] += siz[v];
		}
	};
 
	dfs(dfs, 1, 1);
 
	while (m--) {
		int k;
		cin >> k;
 
		vector<int> a(k);
		for (auto &i : a) {
			cin >> i;
			i = fa[i];
		}
 
		sort(a.begin(), a.end(), [&](auto x, auto y) {
			return dep[x] < dep[y];
		});
 
		bool f = 1;
		for (int i = 1; i < k; i ++) {
			if (dfn[a[i - 1]] <= dfn[a[i]] && dfn[a[i]] < dfn[a[i - 1]] + siz[a[i - 1]])
				continue;
			f = 0;
		}
 
		cout << (f ? "YES" : "NO") << '\n';
	}
 
	return 0;
}

I - 🐕🐕🐕🐕🐕🐕🐕🐕🐕

AtCoder - abc344_f

题意

有一个 \(N \times N\) 的网格，高桥最开始在位置 \((1,1)\)，有 \(0\) 个金币。

假设高桥现在处于位置 \((i,j)\)，每一秒他
可以做出如下选择中的一种：

  • 不移动，获得 \(P_{i,j}\) 的金币。
  • 移动到 \((i,j+1)\)，花费 \(R_{i,j}\) 的金币。
  • 移动到 \((i+1,j)\)，花费 \(D_{i,j}\) 的金币。

高桥在任意位置的金币数都不能小于 \(0\)。

求高桥到达 \((N,N)\) 的最小时间。

思路

获得金币的代价是相同的，那肯定在金币多的地方待着是最优的。

假设在起点待着获得的金币最多，那我完全可以在起点攒够了直接到终点，如果中间某点的金币比我起点还多，那我肯定攒够钱到那个点继续攒嘛\(\dots\)，以此类推，假设选择获得金币的点为 \(a_1,a_2,a_3\dots\)，那么他们能够获得的金币一定是 \(P_{a_i}<P_{a_2}<P_{a_3}\dots\)，时这条路径才是最优的。

设 \(dp_{i,j}\) 表示走到 \((i,j)\) 所需的最少步数和最少花费，用一个 dis 数组辅助计算后从 \((i,j)\) 点到后面的点的花费，然后判断后面的点的 \(P_{x,y}\) 是否大于 \(P_{i,j}\)，有就进行转移。

代码

#include<bits/stdc++.h>
 
using namespace std;
 
using i64 = long long;
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
 
    int n;
    cin >> n;
 
    vector P(n + 1, vector<i64>(n + 1));
    vector R(n + 1, vector<i64>(n + 1, LLONG_MAX >> 1));
    vector D(n + 1, vector<i64>(n + 1, LLONG_MAX >> 1));
 
    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= n; j ++)
            cin >> P[i][j];
 
    for (int i = 1; i <= n; i ++)
        for (int j = 1; j < n; j ++)
            cin >> R[i][j];
 
    for (int i = 1; i < n; i ++)
        for (int j = 1; j <= n; j ++)
            cin >> D[i][j];
 
    vector dp(n + 1, vector<array<i64, 2>>(n + 1, {LLONG_MAX >> 1, 0}));
 
    dp[1][1] = {0, 0};
 
    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= n; j ++) {
 
            vector dis(n + 1, vector<i64>(n + 1, LLONG_MAX >> 1));
 
            dis[i][j] = 0;
            for (int p = i; p <= n; p ++)
                for (int k = j; k <= n; k ++) {
                    if (p > 1) dis[p][k] = min(dis[p][k], dis[p - 1][k] + D[p - 1][k]);
                    if (k > 1) dis[p][k] = min(dis[p][k], dis[p][k - 1] + R[p][k - 1]);
                }
 
 
            for (int p = i; p <= n; p ++)
                for (int k = j; k <= n; k ++) {
                    if (k != n && p != n && P[p][k] < P[i][j]) continue;
 
                    auto [step, money] = dp[i][j];
                    i64 cost = max(0ll, (dis[p][k] - money + P[i][j] - 1) / P[i][j]);
                    i64 Newmoney = money + cost * P[i][j] - dis[p][k];
                    i64 Newstep = step + cost + (p - i + k - j);
                    if (Newstep < dp[p][k][0] || Newstep == dp[p][k][0] && Newmoney > dp[p][k][1]) {
                        dp[p][k] = {Newstep, Newmoney};
                    }
                }
 
        }
 
    cout << dp[n][n][0] << '\n';
 
    return 0;
}

本文作者：Ke_scholar

本文链接：https://www.cnblogs.com/Kescholar/p/18313849

版权声明：本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。

posted @   Ke_scholar  阅读(22)  评论(0)  编辑  收藏  举报
历史上的今天：
2023-07-20 23暑假友谊赛
点击右上角即可分享
微信分享提示
AI IDE Trae
评论
收藏
关注
推荐
深色
回顶
收起