河南萌新联赛2024第（一）场：河南农业大学

河南萌新联赛2024第（一）场：河南农业大学

A-造数_河南萌新联赛2024第（一）场：河南农业大学 (nowcoder.com)

思路

2 的二进制为 10，对于任意一个数，如 13，其二进制为 1101，可由 10 \(\rightarrow\) 100 \(\rightarrow\) 110 \(\rightarrow\) 1100 \(\rightarrow\) 1101，即 +2，×2，+2，×2，+1，即按照二进制来判断需要用多少次加 2 乘 2 ，最后判断需不需要加 1 即可。

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    i64 n;
    cin >> n;

    int ans = 0;
    for (i64 i = 31; i > 0; i --) {
        if (ans) ans ++;
        if ((n >> i) & 1) {
            ans ++;
        }
    }

    cout << ans + (n & 1) << '\n';

    return 0;
}

B-爱探险的朵拉_河南萌新联赛2024第（一）场：河南农业大学 (nowcoder.com)

思路

前置知识： tarjan缩点+拓扑序。

根据题意可以抽象出就是给你一个有向有环图，然后就是用 tarjan 将环缩成点，用拓扑序跑最长路即可。

代码

#include<bits/stdc++.h>

using namespace std;

const int maxn = 1e5 + 15;
int n, m, sum, tim, top, s;
int p[maxn], head[maxn], sd[maxn];
int dfn[maxn], low[maxn];
//DFN(u)为节点u搜索被搜索到时的次序编号(时间戳)，Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号
int stac[maxn], vis[maxn]; //栈只为了表示此时是否有父子关系
int h[maxn], in[maxn], dist[maxn];

vector<int> g[maxn], ng[maxn];

void tarjan(int x) {
    low[x] = dfn[x] = ++tim;
    stac[++top] = x; vis[x] = 1;
    for (auto v : g[x]) {
        if (!dfn[v]) {
            tarjan(v);
            low[x] = min(low[x], low[v]);
        } else if (vis[v]) {
            low[x] = min(low[x], low[v]);
        }
    }
    if (dfn[x] == low[x]) {
        int y;
        while (y = stac[top--]) {
            sd[y] = x;
            vis[y] = 0;
            if (x == y) break;
            p[x] += p[y];
        }
    }
}
int topo() {
    queue <int> q;
    int tot = 0;
    for (int i = 1; i <= n; i++)
        if (sd[i] == i && !in[i]) {
            q.push(i);
            dist[i] = p[i];
        }
    while (!q.empty())
    {
        int k = q.front(); q.pop();
        for (auto v : ng[k]) {
            dist[v] = max(dist[v], dist[k] + p[v]);
            in[v]--;
            if (in[v] == 0) q.push(v);
        }
    }
    int ans = 0;
    for (int i = 1; i <= n; i++)
        ans = max(ans, dist[i]);
    return ans;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n;

    for (int i = 1; i <= n; i ++)
        p[i] = 1;

    vector<int> a(n + 1);
    vector<pair<int, int>> edge;
    for (int i = 1; i <= n; i ++) {
        cin >> a[i];
        edge.push_back({i, a[i]});
        g[i].push_back(a[i]);
    }
    for (int i = 1; i <= n; i++)
        if (!dfn[i]) tarjan(i);
    for (auto &[from, to] : edge) {
        int x = sd[from], y = sd[to];
        if (x != y) {
            ng[x].push_back(y);
            in[y]++;
        }
    }

    cout << topo() << '\n';

    return 0;
}

C-有大家喜欢的零食吗_河南萌新联赛2024第（一）场：河南农业大学 (nowcoder.com)

思路

前置知识：二分图最大匹配，匈牙利算法。

将第 i 个小朋友喜欢的第 j 份零食大礼包看成由 i 向 j 连一条边，问左边的 n 个点能最大匹配右边的多少个点，那么这题就是求二分图的最大匹配数，上板子即可。

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

struct augment_path {
    vector<vector<int> > g;
    vector<int> pa;  // 匹配
    vector<int> pb;
    vector<int> vis;  // 访问
    int n, m;         // 两个点集中的顶点数量
    int dfn;          // 时间戳记
    int res;          // 匹配数

    augment_path(int _n, int _m) : n(_n), m(_m) {
        assert(0 <= n && 0 <= m);
        pa = vector<int>(n, -1);
        pb = vector<int>(m, -1);
        vis = vector<int>(n);
        g.resize(n);
        res = 0;
        dfn = 0;
    }

    void add(int from, int to) {
        assert(0 <= from && from < n && 0 <= to && to < m);
        g[from].push_back(to);
    }

    bool dfs(int v) {
        vis[v] = dfn;
        for (int u : g[v]) {
            if (pb[u] == -1) {
                pb[u] = v;
                pa[v] = u;
                return true;
            }
        }
        for (int u : g[v]) {
            if (vis[pb[u]] != dfn && dfs(pb[u])) {
                pa[v] = u;
                pb[u] = v;
                return true;
            }
        }
        return false;
    }

    int solve() {
        while (true) {
            dfn++;
            int cnt = 0;
            for (int i = 0; i < n; i++) {
                if (pa[i] == -1 && dfs(i)) {
                    cnt++;
                }
            }
            if (cnt == 0) {
                break;
            }
            res += cnt;
        }
        return res;
    }
};

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n;
    cin >> n;

    augment_path ad(n,n);
    for(int i = 0;i < n;i ++){
        int k;
        cin >> k;
        for(int j = 0;j < k;j ++){
            int x;
            cin >> x;
            ad.add(i,--x);
        }
    }

    int res = ad.solve();
    if(res == n){
        cout << "Yes\n";
    }else{
        cout << "No\n" << n - res << '\n';
    }

    return 0;
}

D-小蓝的二进制询问_河南萌新联赛2024第（一）场：河南农业大学 (nowcoder.com)

思路

对于这种给一个区间求种类数的题目，不难想到前缀和的思想。

现考虑求一个数 x 从 1 到 x 的整数的二进制中的 1 的个数之和。

以 25 为例:

可以看出，对于每一位，画红框的地方是每一位的循环节，第 k 位的循环节长度为 \(2^{k+1}\) ，其中有 \(2^k\) 个 1，所以我们可以按位枚举，计算每一位上总共有多少个循环节和剩下非循环节中 1 的个数，因为这里是从 0 开始计算每一位的长度，所以实际计算时 x 需要加 1，具体计算就是，对于第 i 位：

\[\sum_{i=0}^{60}\frac{x+1}{2^{i+1}}\times2^i+\max((x+1)\%2^{i+1}-2^i,0) \]

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

const i64 mod = 998244353;

void solve() {

    i64 l, r;
    cin >> l >> r;

    auto calc = [&](i64 x)->i64{
        i64 res = 0;

        x ++;
        for (int i = 60; i >= 0; i --) {
            i64 y = x / (1ll << (i + 1));
            res = (res + y * (1ll << i) % mod) % mod;
            res = (res + max(x % (1ll << (i + 1)) - (1ll << i), 0ll)) % mod;
        }

        return res % mod;
    };

    cout << (calc(r) - calc(l - 1) + mod) % mod << '\n';

}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int t;
    cin >> t;
    while (t--)
        solve();

    return 0;
}

E-奇妙的脑回路_河南萌新联赛2024第（一）场：河南农业大学 (nowcoder.com)

思路

代码

F-两难抉择新编_河南萌新联赛2024第（一）场：河南农业大学 (nowcoder.com)

思路

对于第 i 个数，直接按 \([1,\frac{n}{i}]\) 的范围枚举两种操作，更新最大值即可。

复杂度 \(O(nln\ n)\)

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n;
    cin >> n;

    i64 ans = 0;
    vector<i64> a(n + 1);
    for (int i = 1; i <= n; i ++) {
        cin >> a[i];
        ans ^= a[i];
    }

    i64 t = ans;
    for (int i = 1; i <= n; i ++) {
        i64 res = t;
        res ^= a[i];
        for (int j = 1; j <= n / i; j ++) {
            ans = max(ans, res ^ (a[i] + j));
        }
        for (int j = 1; j <= n / i; j ++) {
            ans = max(ans, res ^ (a[i] * j));
        }
    }

    cout << ans << '\n';

    return 0;
}

G-旅途的终点_河南萌新联赛2024第（一）场：河南农业大学 (nowcoder.com)

思路

遍历 1 到 n ，用最小堆去维护当前最大的 k 个需要消耗的生命力，当枚举到当前所有消耗的生命力之和减去 k 个最大的也大于了 m 就说明无法继续再往下旅游了，注意会爆longlong，开 int128 即可。

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    i64 n, m, k;
    cin >> n >> m >> k;

    using pii = pair<i64, i64>;
    vector<i64> a(n + 1);
    for (int i = 1; i <= n; i ++) {
        cin >> a[i];
    }

    __int128 Hp = 0, qhp = 0;
    priority_queue<i64, vector<i64>, greater<>> q;

    int ans = 0;
    for (int i = 1; i <= n; i ++) {
        Hp += a[i];
        q.push(a[i]);
        qhp += a[i];
        if (q.size() > k) {
            qhp -= q.top();
            q.pop();
        }
        if (Hp - qhp >= m) break;
        ans = i;
    }

    cout << ans << '\n';

    return 0;
}

H-两难抉择_河南萌新联赛2024第（一）场：河南农业大学 (nowcoder.com)

思路

两种操作都是保证会让原数增大的，所以只要判断下最大值怎么操作即可。

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n;
    cin >> n;

    i64 sum = 0,ma = 0;;
    vector<i64> a(n);
    for(auto &i : a){
        cin >> i;
        sum += i;
        ma = max(ma,i);
    }

    sum += max(ma + n,ma * n) - ma;

    cout << sum << '\n';

    return 0;
}

I-除法移位_河南萌新联赛2024第（一）场：河南农业大学 (nowcoder.com)

思路

按定义化成分数形式可得：\(\frac{a_1}{a_2a_3\dots a_n}\)，要使该式最大化，即分子越大或者让分母越小，所以只要找到右移（倒序）后小于等于 t 的最大值下标即可。

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

struct node {
    int v, id;
};

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    i64 n, t;
    cin >> n >> t;

    vector<node> a(n + 1);
    for (int i = 1; i <= n; i ++) {
        cin >> a[i].v;
        a[i].id = n - i + 1;
    }

    a[1].id = 0;
    sort(a.begin() + 1, a.end(), [](node x, node y) {
        if (x.v == y.v) return x.id < y.id;
        return x.v > y.v;
    });

    for (int i = 1; i <= n; i ++) {
        auto [v, id] = a[i];
        if (id <= t) {
            cout << id << '\n';
            return 0;
        }
    }

    return 0;
}

J-最大矩阵匹配_河南萌新联赛2024第（一）场：河南农业大学 (nowcoder.com)

思路

考虑 dp 。

为了方便线性的转移，可以将矩阵上下翻转，这样就是求 \(\nwarrow\) 的最大边长了。

设 \(dp_{i,j}\) 为 \((i,j)\) 点能够形成的箭头最长长度。

当个为 1 的初始化为 \(dp_{i,j}=1\)，4 个 1 的正方形矩阵初始化为 \(dp_{i,j}=2\)。

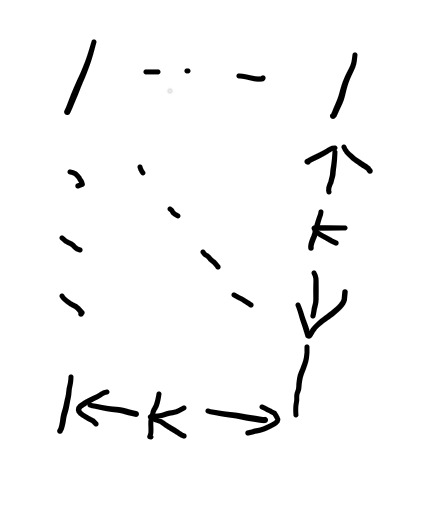
对于这样的 \((i,j)\) 点，一定是 \((i-1,j-1)\) 点先满足条件后它才能继续往下扩展，如果 \(dp_{i-1,j-1}=k\) 即 \((i-1,j-1)\) 点能形成的最大边长为 k 满足条件的矩阵时，那么对于 \((i,j)\) 点就要去判断能否形成 k+1 的边长，具体判断这里要用到二维前缀和和辅助计算矩形内 1 的个数，还要判断第 \((i-k,j)，(i,j-k),(i,j)\) 这三个点是否都为 1才能进行转移。

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, m;
    cin >> n >> m;

    vector a(n + 1, vector<bool>(m + 1));
    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= m; j ++) {
            char c;
            cin >> c;
            a[n + 1 - i][j] = c - '0';
        }

    vector s(n + 1, vector<int>(m + 1));
    for (int i = 1; i <= n; i ++) {
        for (int j = 1; j <= m; j ++) {
            s[i][j] = a[i][j] + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
        }
    }

    auto get = [&](int x1, int y1, int x2, int y2)->int{
        return s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1];
    };

    int ans = 0;
    vector dp(n + 1, vector<int>(m + 1));

    for (int i = 1; i <= n; i ++) {
        for (int j = 1; j <= m; j ++) {
            int k = dp[i - 1][j - 1];
            if (a[i][j] && a[i - 1][j] && a[i][j - 1] && a[i - 1][j - 1])
                dp[i][j] = 2;
            else if (a[i][j])
                dp[i][j] = 1;
            if (a[i][j] && a[i - k][j] && a[i][j - k] && get(i - k, j - k, i, j) == 3 * k + 1)
                dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + 1);
            ans = max(ans, dp[i][j]);
        }
    }

    cout << ans << '\n';

    return 0;
}

K-图上计数(Easy)_河南萌新联赛2024第（一）场：河南农业大学 (nowcoder.com)

思路

因为可以删掉任意边又合并任意联通块，所以直接就想象成给你一堆点，合并成两堆使得其乘积最大，即就是两堆点数接近 \(\frac{n}{2}\) 时最大。

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    i64 n, m;
    cin >> n >> m;

    vector g(n + 1, vector<int>());
    for (int i = 0; i < m; i ++) {
        int u, v;
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }

    cout << (n / 2)*(n - n / 2) << '\n';

    return 0;
}

L-图上计数(Hard)_河南萌新联赛2024第（一）场：河南农业大学 (nowcoder.com)

思路

本题只能断桥，同理，和上一题一样用 tarjan 先断掉所有的桥得到若干个连通块，把每个块的大小塞进数组中，题目就变成了选择其中的一些元素之和使得其与剩下的元素之和的乘积最大，没错，变成了背包问题，但是使用常规的 01 背包会超时，可以观察到所有的元素之和等于 n ，根据 \(\frac{x\times(x+1)}{2}=n\)，所以连通块大小的种类不会超过 \(\sqrt n\)，那么可以统计每个联通块大小的个数，采取二进制或单调队列优化跑多重背包。

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

struct SCC {

    int top = 0, cntscc = 0, dfncnt = 0;
    vector<int> dfn, low, stk, instk;
    vector<int> sccnum, sccid;
    vector<vector<int>> g, scc;
    //割点
    vector<bool> flag, vis;
    //割桥
    vector<int> father;
    vector<bool> isbridge;

    SCC(int n) {
        //缩点
        dfn.assign(n + 1, 0);
        low.assign(n + 1, 0);
        stk.assign(n + 1, 0);
        sccnum.assign(n + 1, 0);
        sccid.assign(n + 1, 0);
        instk.assign(n + 1, 0);
        g.resize(n + 1);
        scc.resize(n + 1);
        //求割点
        flag.assign(n + 1, 0);
        vis.assign(n + 1, 0);
        //求割桥
        father.assign(n + 1, 0);
        isbridge.assign(n + 1, 0);
    }

    void add(int u, int v) {
        g[u].push_back(v);
    }

    //缩点
    void tarjan(int u) {
        dfn[u] = low[u] = ++dfncnt;
        stk[++top] = u;
        instk[u] = 1;

        for (auto v : g[u]) {
            if (!dfn[v]) {
                tarjan(v);
                low[u] = min(low[u], low[v]);
            } else if (instk[v]) {
                low[u] = min(low[u], low[v]);
            }
        }

        if (dfn[u] == low[u]) {
            cntscc ++;
            int v;
            do {
                v = stk[top --], instk[v] = 0;
                sccid[v] = cntscc;
                scc[cntscc].push_back(v);
                sccnum[cntscc] ++;
            } while (u != v);
        }
    }

    void tarjan_GeDian(int u, int fa) { // u 当前点的编号，father 自己爸爸的编号
        vis[u] = 1;
        low[u] = dfn[u] = ++ dfncnt;  // 打上时间戳

        int child = 0;  // 每一个点儿子数量
        for (auto v : g[u]) { // 访问这个点的所有邻居
            if (!vis[v]) {
                child ++; // 多了一个儿子
                tarjan_GeDian(v, u);
                low[u] = min(low[u], low[v]); // 更新能到的最小节点编号
                if (fa != u && low[v] >= dfn[u] && !flag[u]) {
                    // 如果不是自己，且不通过父亲返回的最小点符合割点的要求，并且没有被标记过
                    // 要求即为：删了父亲连不上去了，即为最多连到父亲
                    flag[u] = 1;
                }
            } else if (v != fa) { // 如果这个点不是自己，更新能到的最小节点编号
                low[u] = min(low[u], dfn[v]);
            }
        }
        // 主要代码，自己的话需要 2 个儿子才可以
        if (fa == u && child >= 2 && !flag[u]) {
            flag[u] = 1;
        }
    }

    //当 isbridge[x] 为真时，(father[x],x) 为一条割边。
    int cntbridge = 0;
    void tarjan_GeQiao(int u, int fa) {
        father[u] = fa;
        low[u] = dfn[u] = ++dfncnt;

        for (auto v : g[u]) {
            if (!dfn[v]) {
                tarjan_GeQiao(v, u);
                low[u] = min(low[u], low[v]);
                if (low[v] > dfn[u]) {
                    isbridge[v] = 1;
                    ++ cntbridge;
                }
            } else if (dfn[v] < dfn[u] && v != fa) {
                low[u] = min(low[u], low[v]);
            }
        }
    }
};

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, m;
    cin >> n >> m;

    SCC qiao(n);

    vector<pair<int, int>> edge(m);
    for (int i = 0; i < m; i ++) {
        int u, v;
        cin >> u >> v;
        edge[i] = {u, v};
        qiao.add(u, v);
        qiao.add(v, u);
    }

    for (int i = 1; i <= n; i ++) {
        if (!qiao.dfn[i]) {
            qiao.tarjan_GeQiao(i, i);
        }
    }

    SCC sd(n);
    for (int i = 0; i < m; i ++) {
        auto [u, v] = edge[i];
        if (qiao.isbridge[u] && qiao.father[u] == v || qiao.isbridge[v] && qiao.father[v] == u)
            continue;
        sd.add(u, v);
        sd.add(v, u);
    }

    for (int i = 1; i <= n; i ++) {
        if (!sd.dfn[i]) {
            sd.tarjan(i);
        }
    }

    set<int> object;
    vector<int> num(n + 1);
    for (int i = 1; i <= sd.cntscc; i ++) {
        object.insert(sd.sccnum[i]);
        num[sd.sccnum[i]] ++;
    }

    vector<int> dp(n + 1);

    dp[0] = 1;
    for (auto &i : object) {
        int has = num[i];
        for (int k = 1; k <= has; k <<= 1) {
            has -= k;
            i64 w = k * i;
            for (int j = n; j >= w; j --)
                dp[j] |= dp[j - w];
        }
        if (has) {
            i64 w = has * i;
            for (int j = n; j >= w; j --)
                dp[j] |= dp[j - w];
        }
    }

    i64 ans = 0;
    for (int i = 1; i <= n; i ++) {
        if (dp[i]) {
            ans = max(ans, 1ll * (n - i) * i);
        }
    }

    cout << ans << '\n';

    return 0;
}