SMU Summer 2024 Contest Round 3

寻找素数对

题意

给你一个偶数，找到两个最接近的素数，其和等于该偶数。

思路

处理出 1e5 以内的素数，然后遍历，更新最接近的答案。

代码

 #include<bits/stdc++.h>
 
using namespace std;
 
using i64 = long long;
 
vector<int> euler_range(int n) {
    vector<int> phi(n + 1), prime;
    vector<bool> is_prime(n + 1, true);
    is_prime[1] = 0, phi[1] = 1;
    for (int i = 2; i <= n; i++) {
        if (is_prime[i]) prime.push_back(i), phi[i] = i - 1;
        for (int j = 0; j < (int)prime.size() && i * prime[j] <= n; j++) {
            is_prime[i * prime[j]] = 0;
            if (i % prime[j]) phi[i * prime[j]] = phi[i] * (prime[j] - 1);
            else {
                phi[i * prime[j]] = phi[i] * prime[j];
                break;
            }
        }
    }
    return prime;
}
 
const int N = 1e5;
auto pr = euler_range(N);
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
 
    int x;
    set<int> s(pr.begin(), pr.end());
    while (cin >> x) {
        int a = 0, b = 0;
        for (auto i : pr) {
            if (i > x) break;
            if (s.count(x - i)) {
                if (!a) a = i, b = x - i;
                else if (abs(x - i - i) < abs(a - b))
                    a = i, b = x - i;
            }
        }
        if (a > b) swap(a, b);
        cout << a << ' ' << b << '\n';
    }
 
    return 0;
}

抱歉

题意

平面上有 n 个点，每个点至少有 2 条曲线线段连接，所有曲线线段不相交，但是任意两点之间可以有多条曲线，问你 n 个点将平面分成了 m 份中存在的曲线线段数量。

思路

满足最小的条件，即每个点都能有两条曲线线段相连的图中最少有 n 条线段。

如图：

可以看出，最小符合条件的连线方式将平面分成了 2 份，又因为两点之间可以有多条曲线，所以每增加一个面只需要加一条曲线即可。

如图：

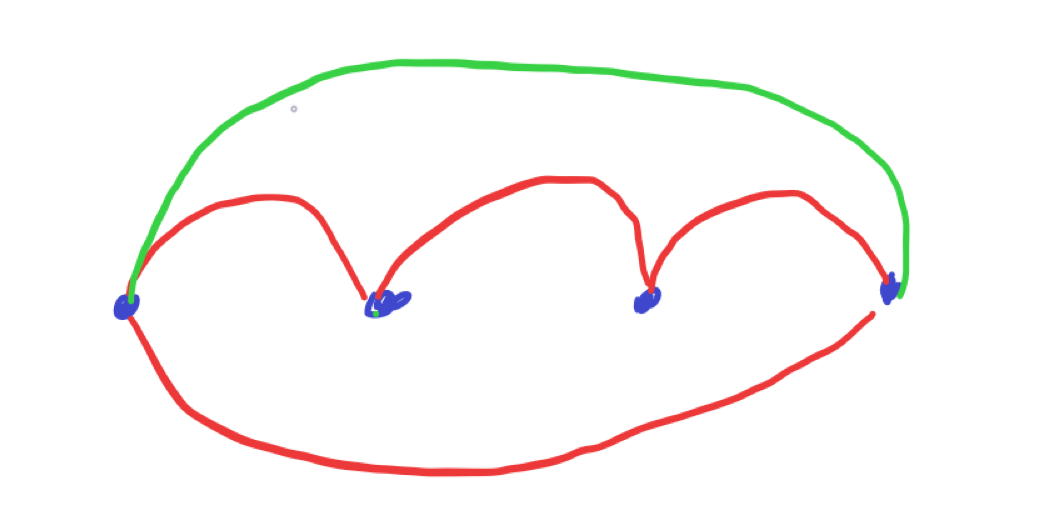
所以答案就是 $n+m-2$，记得开longlong。

代码

 #include<bits/stdc++.h>
 
using namespace std;
 
using i64 = long long;
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
 
    i64 n,m;
    while(cin >> n >> m && n && m){
       	cout << n + m - 2 << '\n';
    }
 
    return 0;
}

搬寝室

题意

从 n 个物品中选出 2k 个物品，每两个物品产生的贡献是其重量差值的平方，求最小的贡献值。

思路

n 个选 2k 个，考虑dp。

因为要求差值的平方最小，所以我们将物品按重量按差值排序，排序后相邻的物品其重量差值相对最小。

然后处理出第 i 个物品与 i + 1 个物品间的差值平方。

设 $dp_{i,j}$ 为前 i 个物品中搬运 j 次的最小贡献。

对于第 i 个物品，如果选择它，则答案是 i-1 物品与它的贡献加上 $dp_{i-2,j-1}$ 时的贡献，如果不选，那答案就等于 $dp_{i-1,j}$ 。

代码

 #include<bits/stdc++.h>
 
using namespace std;
 
using i64 = long long;
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
 
    int n, k;
    while (cin >> n >> k) {
        vector<i64> w(n + 1);
        for (int i = 1; i <= n; i ++)
            cin >> w[i];
 
        sort(w.begin() + 1, w.end());
 
        vector<vector<i64>> dp(n + 1, vector<i64>(k + 1, LLONG_MAX / 2));
 
        vector<int> val(n + 1);
        for (int i = 1; i < n; i ++) {
            val[i] = pow(w[i + 1] - w[i], 2);
        }
 
        for (int i = 0; i <= n; i ++)
            dp[i][0] = 0;
 
        for (int i = 2; i <= n; i ++)
            for (int j = 1; j * 2 <= i && j <= k; j ++) {
                dp[i][j] = min(val[i - 1] + dp[i - 2][j - 1], dp[i - 1][j]);
            }
 
        cout << dp[n][k] << '\n';
    }
 
    return 0;
}

Nuts

题意

累加 n 个数大于 10 的部分。

思路

按题意模拟。

代码

 #include<bits/stdc++.h>
 
using namespace std;
 
using i64 = long long;
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
 
    int n;
    cin >> n;
 
    int ans = 0;
    while (n --) {
        int x;
 
        cin >> x;
        ans += max(0, x - 10);
    }
 
    cout << ans << '\n';
 
    return 0;
}

Happy Birthday! 2

题意

给你一个含有 N 个正整数的序列 A，请你构造两个序列 B 和 C。

设这两个序列长度分别为 𝑥x 和 𝑦y，则应满足：

$1≤𝑥,𝑦≤𝑁$
$1≤𝐵_𝑖,𝐶_𝑖≤𝑁$ 且两序列均严格递增
$B$ 与 $C$ 互异
$∑_{𝑖=1}^𝑥𝐴_{𝐵_𝑖}≡∑_{𝑗=1}^𝑦𝐴_{C_i}( mod 200)$

其中互异的定义：若 $𝑥≠𝑦$ 或 $𝑥=𝑦$ 但存在一个位置 𝑖 使得 $𝐵_𝑖≠𝐶_𝑖$，则 $B$ 与 $C$ 互异。

思路

结论，在 201 个序列中一定存在两个在模 200 的情况余数相等的序列。

证明：若前面 200 个序列的余数两两不等，则第 201 个序列一定与前面某个序列的余数相等。

考虑到当 $n=8$ 时，其子集序列达到了 256，所以我们可以直接枚举其所有子集，找到满足条件的序列，$n < 8$ 时也是直接暴力枚举找到答案即可，$n > 8$ 时必定有解，按照 $n=8$ 的做法即可。

枚举时注意从 1 开始，因为最少要有一个被选。

代码

 #include<bits/stdc++.h>
 
using namespace std;
 
using i64 = long long;
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
 
    int n;
    cin >> n;
 
    const int p = 200;
 
    vector<i64> w(n);
    for (auto &i : w)
        cin >> i;
 
    n = min(n, 8);
 
    map<int, vector<int>> mp;
 
    auto print = [](vector<int> num) {
        cout << num.size() << ' ';
        for (auto i : num)
            cout << i << " \n"[i == num.back()];
    };
 
    for (int i = 1; i < 1 << n; i ++) {
        i64 sum = 0;
        vector<int> tmp;
 
        for (int j = 0; j < n; j ++) {
            if ((i >> j) & 1) {
                sum = (sum + w[j]) % p;
                tmp.push_back(j + 1);
            }
        }
 
        if (mp.count(sum)) {
            cout << "Yes\n";
            print(mp[sum]);
            print(tmp);
            return 0;
        } else
            mp[sum] = tmp;
    }
 
    cout << "No\n";
 
    return 0;
}

Bowls and Dishes

题意

有 n 道菜和 m 个条件限制，每个条件要求第 $A_i$ 道菜和第 $B_i$ 道菜都有人投票才算满足，现有 k 个人，每个人可以在第 $C_i$ 道菜和第 $D_i$ 道菜中选择一个投票，现问你每个人投票后满足条件的菜的数量最多有多少。

思路

因为 k 最大只有 16 ，所以直接枚举即可。

0 表示第 i 个人投 $C_i$ 道菜，1 表示其投 $D_i$ 道菜。

代码

 #include<bits/stdc++.h>
 
using namespace std;
 
using i64 = long long;
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
 
    int n, m;
    cin >> n >> m;
 
    vector<array<int, 2>> ab(m);
    for (auto &[a, b] : ab)
        cin >> a >> b;
 
    int k;
    cin >> k;
    vector<array<int, 2>> cd(k);
    for (auto &[c, d] : cd)
        cin >> c >> d;
 
    int ans = 0;
    for (int i = 0; i < 1 << k; i ++) {
 
        vector<int> dish(n + 1);
        for (int j = 0; j < k; j ++) {
            dish[cd[j][(i >> j) & 1]] ++;
        }
 
        int res = 0;
        for (auto [a, b] : ab)
            res += (dish[a] && dish[b]);
        ans = max(ans, res);
    }
 
    cout << ans << '\n';
 
    return 0;
}

Rush Hour 2

题意

给定一张 𝑛 个点，𝑚 条边的无向图，每条边有两个属性 $c_i,d_i$。

你现在位于点 1，想要前往点 𝑛，现在的时间是 0。当时间为 𝑡 时经过第 𝑖 条边所需的时间是 $c_i+\lfloor \frac{d_i}{t+1}\rfloor $ 。

你可以在城市中停留任意非负整数时间，请求出你到达点 𝑛n 所花费的最短时间，如果无法到达，输出 -1。

思路

假设当前时间为 t，经过第 i 座城市，则当前答案为 $t + c_i+\lfloor \frac{d_i}{t+1}\rfloor$，仔细观察 $t + \frac{d}{t+1}$，转化为 $t+1+\frac{d}{t+1}-1$ ，其实就是中学时常说的对勾函数，当且仅当 $t+1=\sqrt d$ 即 $t=\sqrt d -1$ 时，取得最小值，所以当走到第 i 座城市的时候，判断一下该时的时间有没有到达 $\sqrt d -1$，没有就等到这个时候再走，大于这个时间直接走即可，其余就是普通的 $dijkstra$ 。

代码

 #include<bits/stdc++.h>
 
using namespace std;
 
using i64 = long long;
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
 
    int n, m;
    cin >> n >> m;
 
    vector g(n + 1, vector<array<int, 3>>());
    for (int i = 0; i < m; i ++) {
        int u, v, c, d;
        cin >> u >> v >> c >> d;
        g[u].push_back({v, c, d});
        g[v].push_back({u, c, d});
    }
 
    vector<i64> dis(n + 1, -1);
    using ar2 = array<i64, 2>;
    priority_queue<ar2, vector<ar2>, greater<>> Q;
 
    dis[1] = 0;
    Q.push({0, 1});
 
    while (Q.size()) {
        auto [time, u] = Q.top();
        Q.pop();
 
        if (dis[u] < time) continue;
 
        for (auto &[v, c, d] : g[u]) {
            i64 t = time, okt = round(sqrt(d)) - 1;
            if (t < okt) t = okt;
 
            if (dis[v] == -1 || dis[v] > t + c + d / (t + 1)) {
                dis[v] = t + c + d / (t + 1);
                Q.push({dis[v], v});
            }
        }
    }
 
    cout << dis[n] << '\n';
 
    return 0;
}

Count Descendants

题意

给出一个 $n$ 个点的有根树，节点编号为 $1, 2, \cdots n$，树根为 $1$，第 $i$（$2 \le i \le n$）号节点的父亲是 $p_i$。
给出 $q$ 个查询，第 $i$ 个查询包含 $a_i, b_i$，计算满足以下条件的点 $u$ 的个数：

1、 $a_i$ 位于 $u$ 到 $1$ 的最短路径上（端点也算）；

2、$u$ 到根上的路径恰好有 $b_i$ 条边。
$n, q \le 2 \times 10^5, 0 \le b_i < n$。

思路

前置知识：时间戳——树中的应用 - 岸南 - 博客园 (cnblogs.com)

由第一个条件可知满足条件的节点一定是 $a_i$ 自己或是其子孙，判断其子孙可以采用时间戳，若一个点的 $[Tin_u,Tout_u]$ 被 $[Tin_{a_i},Tout_{a_i}]$ 包含。那么 u 就是 $a_i$ 的子孙节点。

由第二个条件可得，从根节点到 u 的边就是指的 u 在树中的深度。

那么我们按照深度将节点的时间戳存进去，由于 dfs 是深度优先搜索，那么存进去的时间戳一定是升序排列，那么我们只要二分去找到该深度中被 $a_i$ 的时间戳包含的个数就是我们要求的答案了。

代码

 #include<bits/stdc++.h>
 
using namespace std;
 
using i64 = long long;
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
 
    int n;
    cin >> n;
 
    vector g(n + 1, vector<int>());
    for (int i = 2; i <= n; i ++) {
        int x;
        cin >> x;
 
        g[x].push_back(i);
    }
 
    int timer = 0;
    map<int, vector<int>> mp;
    vector<int> tin(n + 1), tout(n + 1);
 
    auto dfs = [&](auto && self, int u, int d)->void{
        tin[u] = timer ++;
        mp[d].push_back(tin[u]);
        for (auto v : g[u]) {
            self(self, v, d + 1);
        }
        tout[u] = timer ++;
    };
 
    dfs(dfs, 1, 0);
 
    int q;
    cin >> q;
    while (q--) {
        int u, d;
        cin >> u >> d;
        auto end = lower_bound(mp[d].begin(), mp[d].end(), tout[u]);
        auto start = lower_bound(mp[d].begin(), mp[d].end(), tin[u]);
        cout << end - start << '\n';
    }
 
    return 0;
}

To 3

题意

给你一个数，问你最少删除其中哪些位后使得该数能够被 3 整除。

思路

因为数最大只有 1e18，也就是最多只有 18 位，那么枚举一下删掉哪些位即可。

代码

 #include<bits/stdc++.h>
 
using namespace std;
 
using i64 = long long;
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
 
    i64 n;
    cin >> n;
 
    i64 ans = -1;
    i64 len = 1, shi = 1, t = n / 10;
    while (t) {
        len ++, shi *= 10, t /= 10;
    }
 
    for (int i = 0; i < 1ll << len; i ++) {
        i64 res = 0, num = 0, t10 = shi;
        for (int j = 0; j < len; j ++) {
            if (!((i >> j) & 1)) res = res * 10 + (n / t10 % 10);
            else num ++;
            t10 /= 10;
        }
 
        if (res && res % 3 == 0) {
            if (ans == -1) ans = num;
            else ans = min(ans, num);
        }
    }
 
    cout << ans << '\n';
 
    return 0;
}

上一篇SMU Summer 2024 Contest Round 2

下一篇2024 暑假友谊赛-热身1

本文作者：Ke_scholar

本文链接：https://www.cnblogs.com/Kescholar/p/18294108

posted @ 2024-07-10 15:10 Ke_scholar 阅读(8) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

	#include<bits/stdc++.h>

	using namespace std;

	using i64 = long long;

	vector<int> euler_range(int n) {
	vector<int> phi(n + 1), prime;
	vector<bool> is_prime(n + 1, true);
	is_prime[1] = 0, phi[1] = 1;
	for (int i = 2; i <= n; i++) {
	if (is_prime[i]) prime.push_back(i), phi[i] = i - 1;
	for (int j = 0; j < (int)prime.size() && i * prime[j] <= n; j++) {
	is_prime[i * prime[j]] = 0;
	if (i % prime[j]) phi[i * prime[j]] = phi[i] * (prime[j] - 1);
	else {
	phi[i * prime[j]] = phi[i] * prime[j];
	break;
	}
	}
	}
	return prime;
	}

	const int N = 1e5;
	auto pr = euler_range(N);

	int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int x;
	set<int> s(pr.begin(), pr.end());
	while (cin >> x) {
	int a = 0, b = 0;
	for (auto i : pr) {
	if (i > x) break;
	if (s.count(x - i)) {
	if (!a) a = i, b = x - i;
	else if (abs(x - i - i) < abs(a - b))
	a = i, b = x - i;
	}
	}
	if (a > b) swap(a, b);
	cout << a << ' ' << b << '\n';
	}

	return 0;
	}

Ke_scholar

SMU Summer 2024 Contest Round 3

SMU Summer 2024 Contest Round 3

寻找素数对

题意

思路

代码

抱歉

题意

思路

代码

搬寝室

题意

思路

代码

Nuts

题意

思路

代码

Happy Birthday! 2

题意

思路

代码

Bowls and Dishes

题意

思路

代码

Rush Hour 2

题意

思路

代码

Count Descendants

题意

思路

代码

To 3

题意

思路

代码

公告

最新随笔

我的标签

合集 (3)

随笔分类 (242)

随笔档案 (228)

阅读排行榜

评论排行榜

推荐排行榜

最新评论