洛谷100题计划(25/100)

洛谷100题计划(25/100)

P1164 小A点菜 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

01背包模版题(?

\(dp[j]\)表示剩\(j\)元时有多少种点菜方案,\(dp[j] = dp[j] + dp[j - a[i]]\)表示原来的(\(dp[j]\))再加上和\(a[i]\)凑一起等于\(j\)的方案数(\(dp[j-a[i]]\)),\(m\)等于\(0\)时方案数为\(1\)

#include <bits/stdc++.h>
#define debug(a) cout<<#a<<"="<<a<<'\n';

using namespace std;
using i64 = long long;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int n, m;
	cin >> n >> m;
	vector<int> a(n), dp(m + 1);
	for (int i = 0; i < n; i ++)
		cin >> a[i];

	dp[0] = 1;
	for (int i = 0; i < n; i ++) {
		for (int j = m; j >= a[i]; j--) {
			dp[j] += dp[j - a[i]];
		}
	}
	
	cout << dp[m] << endl;

	return 0;
}

P1192 台阶问题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

和上题类似,\(dp[i]\)表示第\(i\)级台阶的不同方式数,不过每次可以向上迈\(1 \sim K\)级台阶,所以\(dp[1] \sim dp[k]\)都可以一步到达, \(dp[i]=dp[i]+dp[i-j]\)即表示原来到达第\(i\)级的再加上从\(i-j\)级台阶迈\(j\)个台阶到达的

#include <bits/stdc++.h>
#define debug(a) cout<<#a<<"="<<a<<'\n';

using namespace std;
using i64 = long long;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	const int mod = 1e5 + 3;
	int n,k;
	cin >> n >> k;
    
	vector<int> dp(n + 1,0);
	for(int i = 1;i <= k;i ++)
		dp[i] = 1;
    
	for(int i = 2;i <= n;i ++){
		for(int j = 1;j <= k && i - j >= 0;j ++){
			dp[i] = (dp[i] % mod + dp[i - j] % mod) % mod;
		}
	}

	cout << dp[n] << '\n';

	return 0;
}

P1170 兔八哥与猎人 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

啊这题刚开始以为只要是周围八个方向就行了,wa了一发后发现不对劲,对于猎人这个点,也就是说他与兔子之间只要没有直接相隔一个点都可以看到兔子

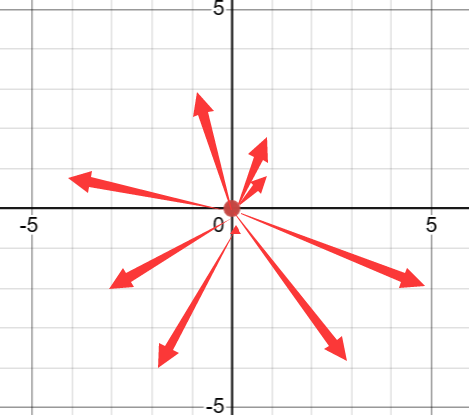
多写几组点后,比如\((1,1),(4,1),(5,4)\)这些都是与\((0,0)\)直接相连且中间线段不会经过一个整数点,也就是一棵树,再细心点就会发现这些点与原点的关系就是\(|ax - bx|\)与\(|ay-by|\)的最大公约数都是\(1\),即\(gcd(|ax-bx|,|ay-by|)=1\)的点都是猎人能直接看到的,所以我们只要判断这个就可以做出这题了,另外对于\(c++14\),可以使用自带的\(\_\_gcd(a,b)\)函数来求最大公约数,而对于\(c++17\),可以使用头文件中的std::gcd来求最大公约数

#include <bits/stdc++.h>
#define debug(a) cout<<#a<<"="<<a<<'\n';

using namespace std;
using i64 = long long;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T;
	cin >> T;
	while(T--){
		int ax,ay,bx,by;
		cin >> ax >> ay >> bx >> by;		

		bool Yes = true;
		if(gcd(abs(ax - bx), abs(ay - by)) == 1) Yes = false;

		cout << (Yes ? "yes" : "no") << '\n';
	}

	return 0;
}

P1181 数列分段 Section I - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

从左向右每超过\(M\)的区段和就单独开一段,记录区间数

#include <bits/stdc++.h>
#define debug(a) cout<<#a<<"="<<a<<'\n';

using namespace std;
using i64 = long long;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int n,m;
	cin >> n >> m;
	vector<int> a(n);
	for(auto &i : a) cin >> i;

	int now = 0, ans = 1;
	for(int i = 0;i < n;i ++){
		if(now + a[i] <= m){
			now += a[i];
		}else{
			now = a[i];
			ans ++;
		}
	}

	cout << ans << '\n';

	return 0;
}

P1364 医院设置 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题意就是说以每个点为中点.求一个距离和(其他每个点到中点的距离再乘以每个点的人口数),可以不用看成一颗树来求,记录每个点的人口数,然后建立一个无向图,每个点遍历一遍,算出以这个点为中心时的距离和,然后找一个最小的即可

#include <bits/stdc++.h>
#define debug(a) cout<<#a<<"="<<a<<'\n';

using namespace std;
using i64 = long long;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int n;
	cin >> n;
	vector<int> w(n + 1);
	vector<vector<int>> G(n + 1);
	for(int i = 1;i <= n;i ++){
		int x,y;
		cin >> w[i] >> x >> y;
		G[i].push_back(x);
		G[i].push_back(y);
		G[x].push_back(i);
		G[y].push_back(i);
	}

	i64 now = 0;
	auto dfs = [&](auto self,int u,int v,int len)->void{
		if(!u) return ;

		for(auto i : G[u]){
			if(i == v) continue;
			self(self,i,u,len + 1);
			now += w[i] * len;
		}
		return ;
	};//就是一个函数

	i64 ans = LLONG_MAX;
	for(int i = 1;i <= n;i ++){
		now = 0;
		dfs(dfs,i,0,1);
		ans = min(ans, now);
	}

	cout << ans << '\n';

	return 0;
}