2023 SMU RoboCom-CAIP 选拔赛

前言

更详细题解可以参考咱学长的(

2023 SMU RoboCom-CAIP 选拔赛.zip

A. 小斧头

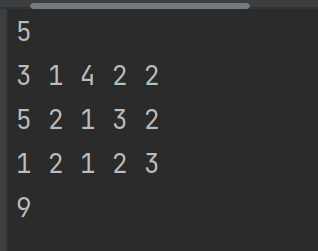
f_k 表示满足条件的j = k 的(i,j)对的数量.如上图中第四行即为f1至f5的元素,f1 = 1即有(1,1)满足条件,f2 = 2即有(1,2),(2,2)满足条件,后面同理,然后要找到一个last_k,即表示k开始向前和向后a数组或b数组最大值发生改变的地方.

得出f_k = last_k + (b[k] >= a[k]) * (k - last_k)

last_k可以用单调栈求出.

 

 

#include  <map>
#include  <set>
#include  <cmath>
#include  <queue>
#include  <stack>
#include  <cstdio>
#include  <vector>
#include  <climits>
#include  <cstring>
#include  <cstdlib>
#include  <iostream>
#include  <algorithm>
#define inf 0x3f3f3f3f
#define endl '\n'
#define int long long

using namespace std;

const int N = 1e5 + 10, mod = 1e9 +7;

//typedef long long ll;
typedef pair<int,int> PII;
//queue<PII> q1;
map<vector<int>, int > mp;
//priority_queue <int,vector<int>,greater<int> > q2;
int n,m,t,k;
/*
*/
int ans;
void solve()
{
    cin >> n;
    vector<int> a(n + 1), b(n + 1), c(n + 1),f(n + 1);
    for (int i = 1; i <=n ; ++i) {
        cin >> a[i];
    }
    for (int i = 1; i <= n ; ++i) {
        cin >> b[i];
    }
    for (int i = 1; i <= n ; ++i) {
        c[i] = max(a[i], b[i]);
    }
    stack<int> stk1, stk2;
    int lst;
    for (int i = 1; i <= n ; ++i) {
        while(!stk1.empty() && a[i] > c[stk1.top()])
            stk1.pop();
        while(!stk2.empty() && b[i] > c[stk2.top()])
            stk2.pop();
        if(b[i] >= a[i]){
            if(stk2.empty())
                lst = 0;
            else
                lst = stk2.top();
            f[i] = f[lst] + i - lst;
        }
        else{
            if(stk1.empty())
                lst = 0;
            else
                lst = stk1.top();
            f[i] = f[lst];
        }
        ans += f[i];
        stk1.push(i);
        stk2.push(i);
    }
//    for(auto i : f)
//        cout << i << ' ';
//    cout << endl;
    cout << ans << endl;
    return ;
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int Ke_scholar = 1;
    //cin >> Ke_scholar ;
    while(Ke_scholar--)
        solve();
    return 0;
}

 

B. 能不能整除?

蒟蒻只会40分做法,学长的有一百分做法(不过咱没看懂QAQ

 40分:就是去统计一下每种A[i] / A[j]出现的次数

#include <bits/stdc++.h>
#define endl '\n'
#define int long long
#define  inf 0x3f3f3f3f

using namespace std;
const int N = 2e3 + 10;

//typedef long long ll;
typedef pair<int,int> PII;
//queue<PII> q1;
map<int, int > mp;
int n,m,t,k;
int c;
priority_queue <int,vector<int>,greater<int> > C;
/*
*/
int mod,ans;
vector<int> a;
void solve()
{
    cin >> n >> t >> mod;
    for(int i = 0;i < n;i ++){
      int x;
      cin >> x;
      a.push_back(x);
    }
    for(auto i : a){
        for(auto j : a)
            mp[i / j] ++;
    }
    for(auto [i,j] : mp){
        if(mp.find(t - i) != mp.end()){
            ans = (ans + j % mod * (mp.find(t - i)->second % mod)) % mod;
        }
    }
    cout << ans << endl;
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);cout.tie(nullptr);
    int Ke_scholar = 1;
    //cin >> Ke_scholar;
    while(Ke_scholar--)
        solve();
    return 0;
}

 

 

C. 又是一道构造题

实际上就是构造的矩阵中每一个元素是a,b数组中的公因数,构造完后再对该矩阵每行每列的乘积判断一下,不合理直接输出-1退出即可.

#include  <map>
#include  <set>
#include  <cmath>
#include  <queue>
#include  <cstdio>
#include  <vector>
#include  <climits>
#include  <cstring>
#include  <cstdlib>
#include  <iostream>
#include  <algorithm>
#define inf 0x3f3f3f3f
#define endl '\n'
#define int long long

using namespace std;

const int N = 2e4 + 10, mod = 1e9 +7;

//typedef long long ll;
typedef pair<int,int> PII;
//queue<PII> q1;
map<vector<int>, int > mp;
vector<int> a,b;
//priority_queue <int,vector<int>,greater<int> > q2;
int n,m,t,k;
/**/
int ans;

void solve()
{
    a.clear();
    b.clear();
    ans = 0;
    cin >> n >> m;
    vector<vector<int> > ma(n,vector<int>(m,0));
    for(int i = 0;i < n; i++){
        int x;
        cin >> x;
        a.push_back(x);
    }
    for(int i = 0;i < m;i ++){
        int x;
        cin >> x;
        b.push_back(x);
    }
    auto g = a;
    auto gg = b;
    for(int i = 0;i < n;i ++){
        for(int j = 0;j < m;j ++){
            int x = __gcd(a[i],b[j]);
            a[i] /= x;
            b[j] /= x;
            ma[i][j] = x;
        }
    }
    for(int i = 0;i < n;i ++){
        int c = 1;
        for(int j = 0;j < m;j ++){
            c *= ma[i][j];
        }
        if(c != g[i]){
            cout << -1 << endl;
            return ;
        }
    }
    for(int i = 0;i < m;i ++){
        int c = 1;
        for(int j = 0;j < n;j ++){
            c *= ma[j][i];
        }
        if(c != gg[i]){
            cout << -1 << endl;
            return ;
        }
    }
    for(auto i : ma){
        for(auto j : i){
            cout << j << ' ';
        }
        cout << endl;
    }
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int Ke_scholar = 1;
    cin >> Ke_scholar ;
    while(Ke_scholar--){
        solve();
        cout << endl;
    }
    return 0;
}