SMU Spring 2023 Contest Round 3(2023年湘潭大学新生赛)

Problem A. 签到啦

从大到小排序,累加大于行李w时输出下标即可

int ans;
void solve()
{
    cin >> n >> m;
    int ans = 0;
    vector<int> a(n);
    for(int i = 0;i < n;i ++){
        cin >> a[i];
    }
    sort(a.begin(), a.end());
    reverse(a.begin(),a.end());
    for(int i = 0;i < n; i++ ){
        ans += a[i];
        if(ans >= m){
            cout << i + 1 << endl;
            return;
        }
    }
}

 

 Problem B. 熙巨打票

冷却时间小于操作时间时,实际上就等于操作时间乘以票数,大于操作时间时,假设操作时间4分钟,冷却时间10分钟,在两台上操作完后还需要等6分钟才能进行操作,6分钟后加上第一台操作完毕的时间刚好10分钟这时第二台又可以操作了,如此往复,票数是奇数时除以2就是要等待的次数,偶数时需减一次,因为最后一次出完后不需要再等待了.

void solve() {
   int a,b,n;
   cin >> a >> b >> n;
   if(a <= b){
       cout << b * n << endl;
       return ;
   }
   else{
       if(n & 1){
           cout << b * n + (n>>1) * (a - b) << endl;
       }
       else{
           cout << b * n + ((n >> 1) - 1) * (a - b) << endl;
       }
   }
}

 

 Problem C. 三元分配

按题意我们可以先分成四种情况,即(以下奇数简称奇,偶数简称偶)奇奇奇,奇奇偶,奇偶偶,偶偶偶,其中奇奇奇和奇偶偶一定是不能配对的,偶偶偶是一定可以配对,所以我们要对奇奇偶这种情况再讨论,因为两个部门要凑成质数才可以进行配对,而两个奇数加起来是质数只能是两个1,且两个1加一个偶数是一定可以配对的,另外再讨论两个奇数与偶数配对成质数的情况即可,当偶数是0时,这时就变成了两个奇数配对了,此时要特判一下

 

 

 

 

bool f(int x){
    if(x < 2)
        return false;
    if(x == 2)
        return true;
    for(int i = 2;i <= sqrt(x);i ++)
        if(x % i == 0)
            return false;
    return true;
}
void solve()
{
    cin >> n >> m >> k;
    if((n + m + k) & 1){
        cout << 'P' << endl;
        return ;
    }
    if(n % 2 == 0 && m % 2 == 0 && k % 2 == 0){
        cout << 'R' << endl;
        return ;
    }
    if(n == 1 && m == 1 || n == 1 && k == 1 || m == 1 && k == 1){
        cout << 'R' << endl;
        return ;
    }
    if(f(n + m) && f(n + k) &&n != 0 || f(m + n) && f(m + k) && m != 0 || f(k + n) && f(k + m) && k != 0){
        cout << 'R' << endl;
        return ;
    }
    cout << 'P' << endl;
    return ;
}

 

Problem D. "逆"天求和

哎,还特意查了一下逆元的公式啥的,最后发现这道题要做的话感觉又和逆元没啥关系

 

感兴趣的可以自己推到一下,就是说当p为质数时,其1到p-1的逆元都在1到p-1中且互不重复

所以我们直接1到p-1累加即可

void solve()
{
    cin >> n;
    int sum = 0;
    for(int i = 1;i < n;i ++){
        sum += i; 
    } 
    cout << sum << endl;
}

 

 

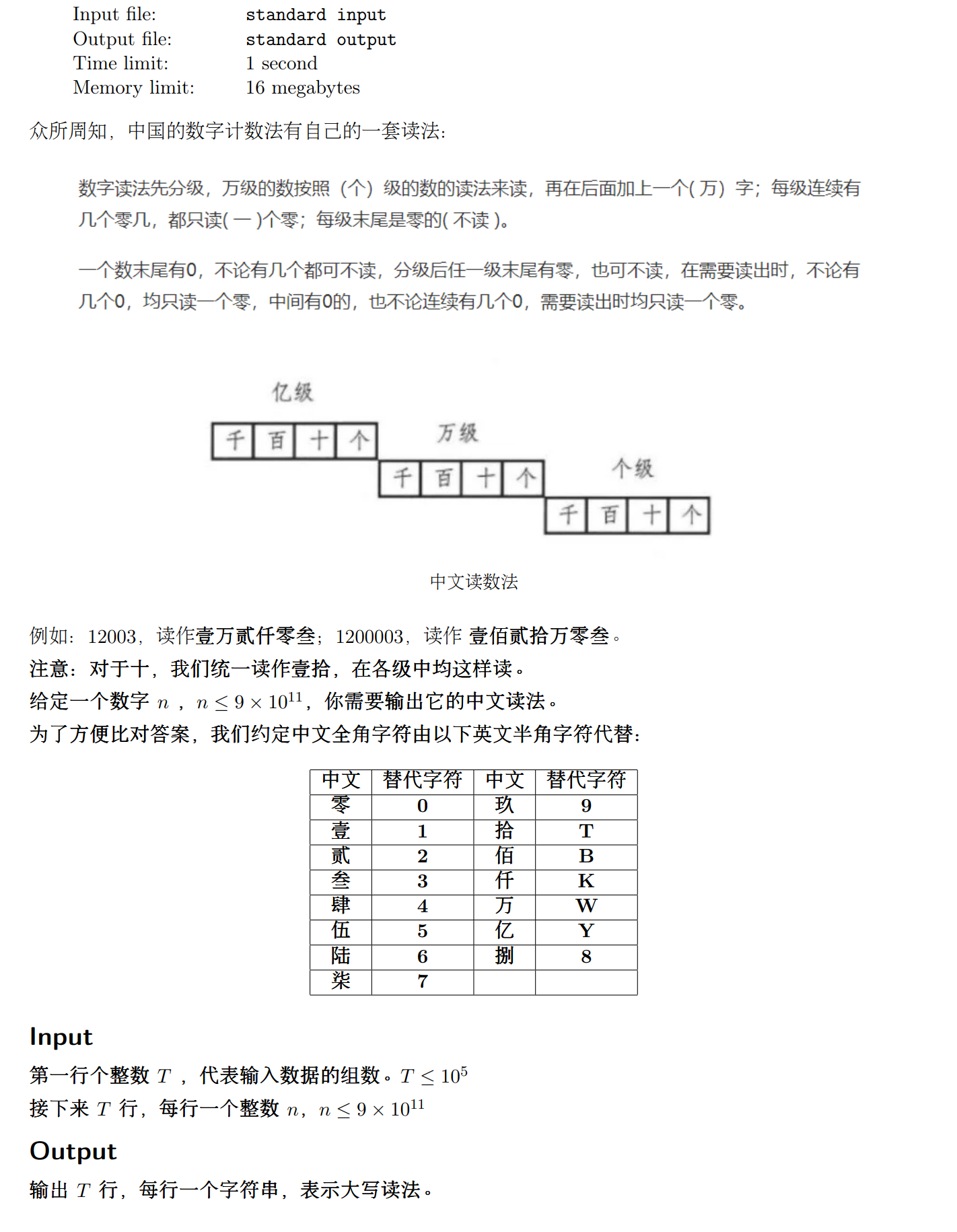
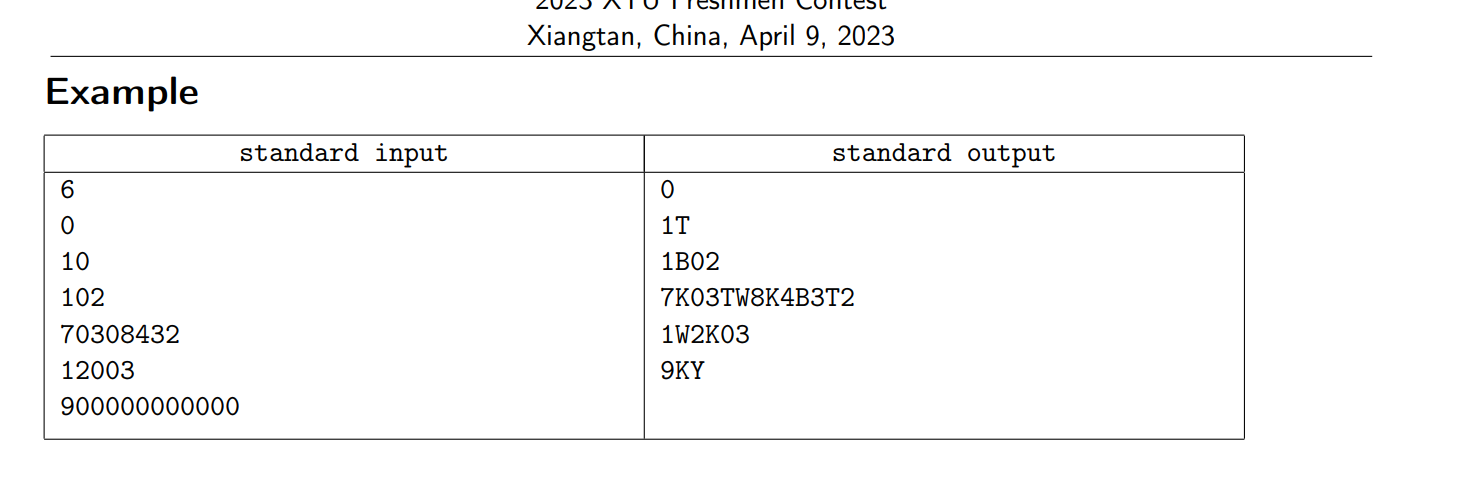
Problem E. 读中国数字

纯模拟,不想多说(

 

#include  <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define endl '\n'
#define int long long

using namespace std;

const int N = 1e5 + 10, mod = 1e9 +7;

//typedef long long ll;
typedef pair<int,int> PII;
//queue<PII> q1;
//priority_queue <int,vector<int>,greater<int> > q2;
int n,m,t,k;
/*
*/
int ans;
void solve()
{
    string num;
    cin >> num;
    if(num == "0"){
        cout << num << endl;
        return ;
    }
    string chinese = "";
    string unit[] = {"", "T", "B", "K", "W", "Y"};
    string digit[] = {"0", "1", "2", "3", "4", "5", "6", "7", "8", "9"};
    int len = num.length();
    int i = 0;
    while (i < len) {
        int j = len - i - 1;
        int k = j % 4;
        bool fw = false,fy = false;
        if (num[i] == '0') {
            int zeroCount = 0;
            bool f = false;
            while (i < len && num[i] == '0') {
                i++;
                if((len - i) == 8 && !fy){
                    chinese += "Y";
                    f = true;
                    fy = true;
                }
                if((len - i) == 4 && !f && !fw && chinese.back() != 'Y'){
                    chinese += "W";
                    f = true;
                    fw = true;
                }
                zeroCount++;
            }
            if (j == 4 && !f && !fw) {
                chinese += "W";
            } else if (j == 8 && !f && !fy) {
                chinese += "Y";
            }
            if(zeroCount >= 1 && i != len && (len - i) != 4 && (len - i) != 8)
                chinese += '0';
        } else {
            chinese += digit[num[i] - '0'] + unit[k];
            if (j == 4 && !fw) {
                chinese += "W";
                fw = true;
            } else if (j == 8 && !fy) {
                chinese += "Y";
                fy = true;
            }
            i++;
        }
    }
    cout << chinese << endl;
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int Ke_scholar = 1;
    cin >> Ke_scholar ;
    while(Ke_scholar--)
        solve();
    return 0;
}

 

 Problem H. 我爱XTU

可以每次计算x,t,u的数量,用pair对其中两个的差进行一个存储,如果这个pair前面出现过,说明从前面到现在有加了x,t,u数量相同的子串,需要注意的当x,t,u数量相等的时候需要加一次,或者在最开始就往pair对里放一组{0,0}.

 

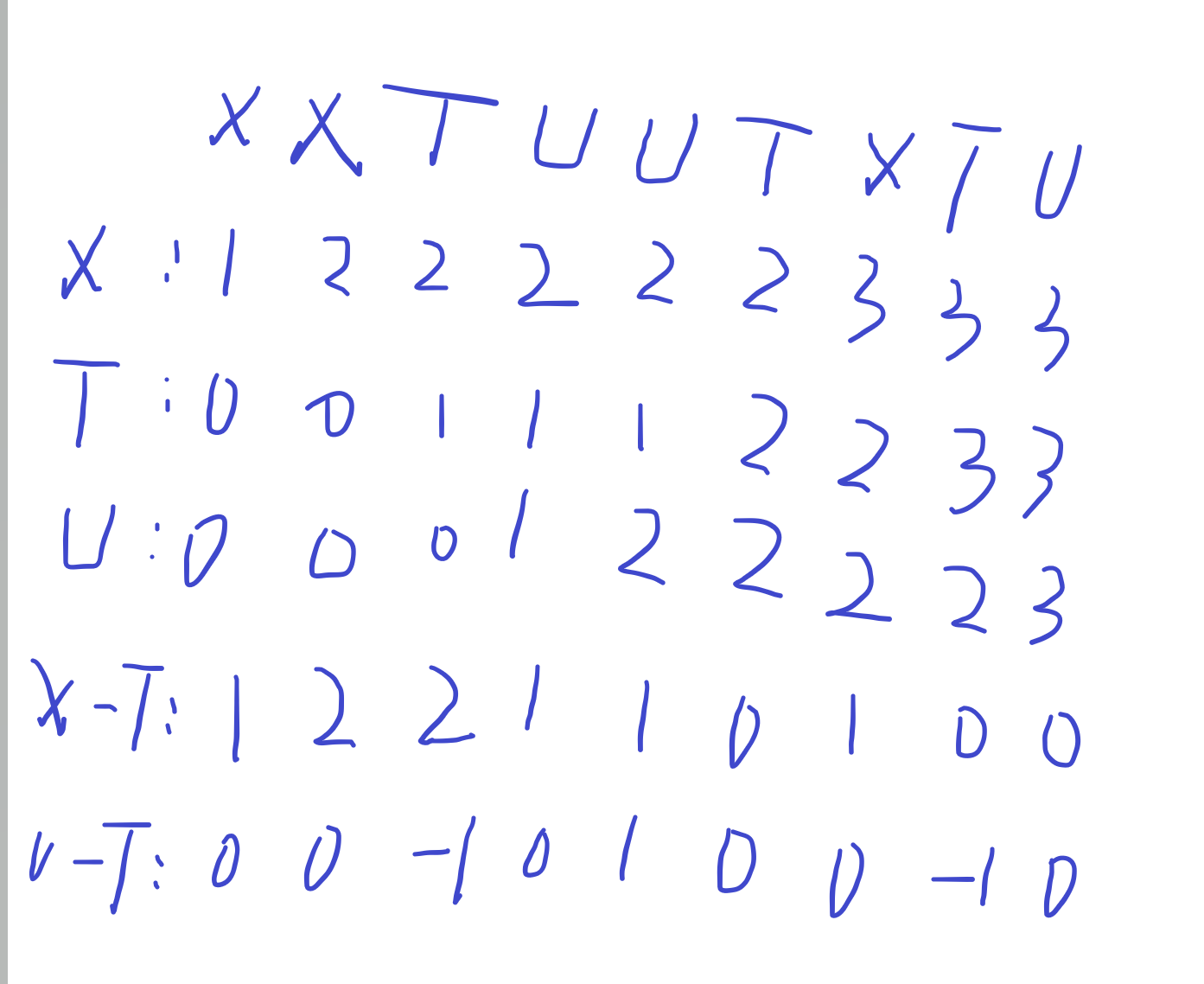
#include  <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define endl '\n'
#define int long long

using namespace std;

const int N = 1e5 + 10, mod = 1e9 +7;

//typedef long long ll;
typedef pair<int,int> PII;
//queue<PII> q1;
//priority_queue <int,vector<int>,greater<int> > q2;
int n,m,t,k;
/*
*/
int ans;
void solve()
{
    string s;
    cin >> s;
    ans = 0;
    int x = 0, t = 0, u = 0;
    map<PII, int> mp;
    for(int i = 0;i < s.size();i ++){
        if(s[i] == 'X')
            x ++;
        else if(s[i] == 'T')
            t ++;
        else
            u ++;
        int divx = x - t;
        int divu = u - t;
        if(x == t && t == u)
            ans ++;
        if(mp.count({divx,divu})){
            ans += mp[{divx, divu}];
           // cout << x << ' ' << t << ' ' << u << endl;
        }
        mp[{divx,divu}]++;
    }
    cout << ans << endl;
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int Ke_scholar = 1;
    cin >> Ke_scholar ;
    while(Ke_scholar--)
        solve();
    return 0;
}