Graph Algorithm

1、定义

A graph consists of a set of vertices V and a set of edges E.

Each edge is a pair (v, w), where v,w belong to V. 

 

路径 A path in a graph is a sequence of vertices w1, w2, ... ,wn.

长度 The length of such a path is the number of edges on the path, which is equal to N-1.

 

权 Sometimes an edge has a third component, known as either a weight or a cost. 

 

Spanning tree 生成树

假设一个连通图有N 个顶点和e条边，其中n-1 条边和n个顶点构成一个极小连通子图，称该极小连通子图为此树的生成树

 

2、图的储存表示

1）邻接矩阵表示法

顶点表：记录各个顶点信息的一位数组

邻接矩阵：一个表示各个顶点之间的关系（边或弧）的二维数组。

const MAX_NUM=20;   //最大顶点数
typedef int AdjMatrix[MAX_NUM][MAX_NUM];  //邻接矩阵

typedef struct
{
	VertexType vexs[MAX_NUM]; //顶点表
	AdjMatrix arcs;  //邻接矩阵
	int vexnum, arcnum; //图实际顶点数与弧数
}MGraph;

在无向图中，第i行（列）1的个数就是顶点i的度。

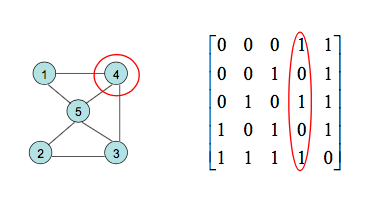
无向图的邻接矩阵是对称的；

有向图的邻接矩阵可能是不对称的。

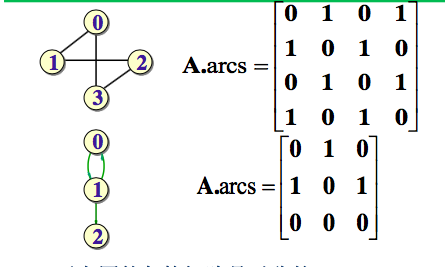
在有向图中，第i行1的个数就是顶点i的出度，第j列1的个数就是j的入度

如果有权值的存在，则也可以在邻接矩阵上加上

 

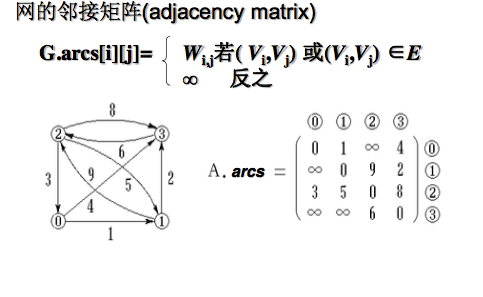
2）邻接表

以一种链式结构形式的存储结构

 

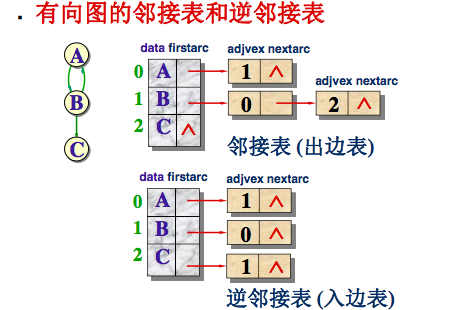
typedef struct ArcNode
{
	int ajdvex; //该弧所指向结点的位置
    ArcNode* nextArc;  //指向下一条弧指针
    InfoNode info;  //弧所带信息，可以是权值
}ArcNode;

typedef struct VNode
{
    VertexType data; //顶点信息
    ArcNode* firstArc;  //指向第一条依附该结点的弧的位置
}VNode, Adjist[MAX_NUM][MAX_NUM];

typedef struct
{
	Adjist verties;  //邻接表
	int vexnum, arcnum;
	int kind; //图的种类
}ALgraph;

　　

带权图的边结点中info保存改变上的权值。

顶点Vi的边链表的头结点存放在下标为i的顶点数组中。

在邻接表的边链表中，各个边结点的链入顺序任意，视边结点输入次序而定。

设图中有n个结点，e条边，则用邻接表表示无向图时，需要n个顶点结点，2*e个边结点；

用邻接表表示有向图时，若不考虑你邻接表，只需n个顶点结点，e个边结点。

建立邻接表的时间复杂度为O(n*e)，若顶点信息为顶点的下标，则时间复杂度为O(n+e).

 

3、图的遍历

从图的某一个顶点出发访问遍图中其余顶点，且使每个顶点仅被访问过一次，就叫做图的遍历。

为避免重复访问，可设置一个表示顶点是否被访问过的辅助数组visited[]，它的初始状态设置为0，一旦某个结点被访问过则立即让对应的visited[i]=1

 

1）DFS 深度优先搜索

算法思想：

从图的某一结点v开始，由v出发，访问它的任一邻接顶点w1；再从w1出发，访问与w1邻接但还没有访问过的顶点w2；再从w2出发，进行类似的访问，…… 如此进行下去，直至到达所有的邻接顶点都被访问过的顶点u为止。接着，退回一步，退到前一次刚访问过的顶点，看是否还有其他没有访问过的邻接顶点。如果有，则访问此顶点，之后再从此顶点出发，进行与上述类似的访问；如果没有，就在退回一步进行搜索，重复上述过程，直到连通图中所有顶点都被访问过为止。（贪心算法？）

 

进一步描述：

（1）从图中某个顶点v出发，访问之；

（2）依次从顶点v的未被访问过的邻接点出发，深度优先遍历图，直到图中所有和顶点v有路径相同的顶点都被访问到；

（3）若此时图中尚有顶点未被访问到，则另选一个未被访问过的顶点作起始点，重复上述（1）（2）的操作，直到图中所哟的顶点都被访问到为止。

//DFS
//遍历算法
void Graph_Traverse(AdjGraph G)
{
	int* visited = new int[NumVertices];
	for(int i=0; i<G.n;i++)
		visiter[i]=0; //访问数组visited初始化
	for(int i=0;i<G.n;i++)
		if(!visited[i])DFS(G, i, visited);

	delete[] visited;
}

void DFS(AdjGraph G, int v, int visited[])
{
	cout<<GetValue(G,v)<<" "<<endl; //访问顶点v
    visited[v]=1;
    int w=GetFirstNeighbor(G,v); //取v的第一个邻接顶点w
    while(w!=-1)
    {
    	if(!visited[w])DFS(G,w,visited);  //若顶点w未访问过，递归访问顶点w
    	w=GetNextNeighbor(G,v,w);  //取顶点v排在w后下一个邻接顶点
    }
}

　　

图中有n个顶点，e条边。

如果用邻接表表示图，沿Firstarc->nextarc 链可以找到某个顶点v 的所有邻接顶点w。由于总共有2e个边结点，所以扫描边的时间为O(e)，而且对所有顶点递归访问1次，时间复杂度为O(n+e)

 

如果用邻接矩阵表示图，则查找每一个顶点的所有的边，所需时间为O(n)，则时间复杂度为O(n^2).

 

2) 广度优先搜索BFS

算法思想：

访问了起始顶点v后，由v出发，依次访问v的各个未被访问过的邻接顶点w1, w2, w3,..., wt, 然后在顺序访问w1, w2, ... ,wt的所有还未被访问过的邻接顶点。再从这些访问过的邻接顶点出发，再访问它们的所有还未被访问过的邻接顶点，……如此做下去，直到图中所有顶点都被访问到为止。

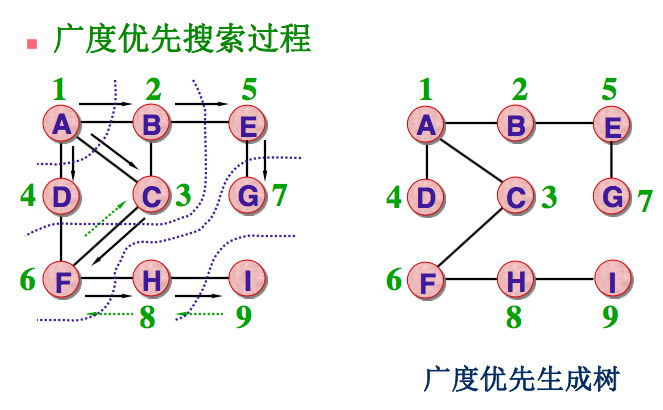
进一步描述：

（1）从图中的某个顶点v出发，访问之；

（2）依次访问顶点v的各个未被访问过的邻接点，将v的全部邻接点都访问到；

（3）分别从这些邻接点出发，依次访问它们的未被访问过的邻接点，并使“先被访问过的顶点的邻接点” 先于“后被访问的顶点的邻接点”被访问，直到图中所有已被访问过的顶点的邻接点都被访问到。

 

//BFS
void Graph_Traverse(AdjGraph G)
{
	int* visited = new int[NumVertices];
	for(int i=0; i<G.n;i++)
		visited[i]=0;
	for(int i=0;i<G.n;i++)
		if(!visited[i])BFS(G,i,visited);

	delete[] visited;
}

void BFS(AdjGraph G, int v, int visited[])
{
	cout<<GetValue(G, v)<<" "<<endl;  //访问结点
	Queue<int>q;   //用队列来储存着一层正在访问的结点
	InitQueue(&q);
	EnQueue(&q,v); //进队列
	while(!QueueEmpty(&q))
	{
		Dequeue(&q,v);
		int w = GetFirstNeighbor(G,v);
		while(w!=-1)
		{
			if(!visited[w])
			{
				cout<<GetValue(G, w)<<" "<<endl;
			    visited[w]=1;
			    EnQueue(&q, w);
			}
			w=GetNextNeighbor(G,v,w);
		}
	}
	delete[] visited;
}

　　

算法分析：

如果使用邻接表表示图，则循环的总时间代价为d0+d1+d2+ ... +d(n-1)=O(e)，其中的di是顶点i的度。

如果使用邻接矩阵，则对于每一个被访问过的顶点，循环要检测矩阵中的n个元素，总的时间代价为O(n^2).