APIO 历年真题乱做

VP 做题就是舒服……知道题目大致难度，知道大家得分分布，写挂了马上能看到评测结果。

就是不知道对临场水平提升有没有太大的帮助。

2020

100+100+10，金。

补题进度：100+100+100。

A

感觉有一车紫严格大于这个东西。

首先你要看懂题，我试了，没有样例解释根本读不懂！

在真正理解题意之后，我们考虑，这个题实际上是两部分。

• 求出能够进行粉刷的起点；

• 利用这些起点，每次可以用线段 \([i,i+m-1]\) 覆盖原序列，最小化覆盖原序列所需的线段条数，或者报告无解。

第二个部分是一个普及组贪心，不再赘述。

现在考虑第一个部分怎么做。

考虑一个最朴素的 DP，设 \(f_{i,j}\) 表示第 \(i\) 位置用第 \(j\) 个粉刷商所能粉刷的最长长度。

不难得到转移：

• \(f_{i,j}=0\)，第 \(i\) 个位置不能用第 \(j\) 个商人刷；

• \(f_{i,j}=f_{i+1,(j+1)\bmod m}+1\)，第 \(i\) 个位置能用第 \(j\) 个商人刷。

另外令 \(g_i=\max_{j=0}^{m-1} f_{i,j}\)，那么 \(i\) 能作为起点的充要条件为 \(g_i=m\)。

然后这个 DP 看起来就有很多空状态，结合 \(f(k)\) 很小的性质，我们提前处理出能够粉刷出第 \(i\) 个位置的商人，只转移这些 \(j\) 就行。

DP 数组用 umap 存。

复杂度 \(O(能过)\)，仔细分析起来太复杂了。

总结：成功签到。

B

挺有意思。

一看到瓶颈路优先想 kruskal 重构树。

然后考虑这个两车不能相遇的限制是吓人的，我们只要 \(x\) 和 \(y\) 所在的连通块不是链就一定能满足条件。

证明考虑分两种情况讨论：

• 如果存在一个度数至少为 \(3\) 的节点，然后 \(x\) 车到这个节点的第三条出边上，让 \(y\) 车先过，然后 \(x\) 车再过，相当于错车。

• 如果不存在这样的点，那么连通块一定是环，也就是说存在两条 \(x \to y\) 的不相交的路径。

于是考虑魔改 kruskal 重构树。

连通块是否为链是容易用并查集维护的，我们只需要记录链首和链尾，对于以下任意一种情况，都是链 \(\to\) 非链：

• 合并两个连通块，至少有一个不是链；

• 合并两个连通块，两个链不能首尾相接；

• 连通块内出现环。

如果任意时刻链 \(\to\) 非链，那么我们暴力将这个连通块内所有的点的点权都赋为当前边权，表示到加入这条边以后这个连通块才合法。因此我们还需要维护连通块内的点，合并时启发式合并即可。

考虑什么时候无解：

• \(x\) 和 \(y\) 不连通；

• \(x\) 和 \(y\) 所在的连通块是链。

复杂度 \(O(n \log n)\)。

总结：这个魔改挺有新意，题面看起来也很可做。

C

\(O(n^2)\) 还原原树，然后爆搜合法排列。

因为合法状态数并不是很多，可以获得 10 分的高分。

哎哎感觉正解不难想，当时纯摆了就没咋想。

首先考虑如果我们 \(O(n^2)\) 还原原树之后，怎么构造出合法的排列。

考虑选取一点为根，我们从它的儿子子树内，从深度最大的点开始，交替选取在不同儿子子树内的点，这样一定可以满足要求。

问题是如果这个根的儿子子树太大的话，它是不能和别的点配对的。

于是我们想到这个根应当是树的重心。

现在考虑不能 \(O(n^2)\) 还原树了，我们怎么求出重心，每个点所在的儿子子树，每个点的深度这三个信息。

首先要求重心。

随机取一点为根，考虑 bow 式重心，也就是满足 \(2size_x \ge n\) 的点中，\(size_x\) 最小的一个，我们用 \(n-1\) 次询问求出子树和即可。

求出重心之后，可以用 \(n-1\) 次询问求出每个点的深度。

最后考虑判断每个点在哪个子树内，因为每个点的儿子个数至多为 \(3\)，所以我们可以询问每个点和重心儿子之间的距离，用深度判断是否在这个儿子的子树内即可，这样的询问次数不会超过 \(2(n-1)\)。

这样我们用 \(4(n-1)\) 次询问获得了我们所有想要的信息，然后直接套上面的构造即可。

2021

3+100+100，金。

补题进度：3+100+100。

A

暴力都不想写。

返回 A 可以获得 3 分的高分。

后来听说了一点正解，根本不想补，就咕了吧。

B

第个位数次独立切黑，有点激动。

但是说实话感觉这个题不如 C 难。

首先考虑，我们的最优策略大概长什么样子，用模糊的语言描述大概是先在左侧左右乱跳，然后到一定高度了之后一路向右跳跳到终点区间。

设 \(val_1=\max_{i=B}^{C-1} h_i\)，\(val_2=\max_{i=C}^{D} h_i\)，那么有解肯定需要保证 \(val_1<val_2\)，可以把这个作为进一步思考的条件。

于是我们想到了一种贪心策略：从 \([A,B]\) 的最高点开始跳，哪边高跳哪边，直到跳出 \(val_1\) 的限制，或者是再跳就超出了 \(val_2\) 的限制，然后一路向右跳到答案。

这个贪心策略怎么想怎么对，每次在能跳最高的时候不跳最高的，只会使得答案变劣。

于是我们进行一点细致的讨论，假设当前能跳的左右两边里，较高的点为 \(x\)：

• \(h_x \le val_1\)，那么肯定跳 \(x\)；

• \(val_1<h_x \le val_2\)，如果 \(x \in [C,D]\)，那么一步到位，否则两步到位；

• \(h_x>val_2\)，那么我们一路向右跳。

一三两个部分都可以倍增处理，具体地，设 \(f_{i,j}\) 表示从 \(i\) 开始任意方向跳 \(2^j\) 步到达的最高高度所在节点，\(g_{i,j}\) 表示只能向右跳的最高节点，那么我们相当于是先跳 \(f\)，达到高度之后我们再判断是第二类情况还是第三类情况，如果是第三类那么我们接着跳 \(g\)。

注意一点细节，如果最开始 \([A,B]\) 的最高点高度 \(>val_2\)，那么我们不能选最高点为起点，我们选 \(g_{x,0}\) 最大的点，然后一直跳 \(g\)。

复杂度 \(O(n \log n)\)。

总结：比较传统的贪心题，思路也有迹可循，不算太 ad-hoc，应该没人说我是 dd 吧？

C

提供一种 lcx 都写不挂的方法。

首先最小化要考虑初始化问题，所以我们把它转化为最大化，也就是最大化保留边的边权和。

然后发现不同的 \(k\) 是独立的，我们先思考对于单个 \(k\) 怎么做。

不难想到一个 DP，设 \(f_{x,0/1}\) 表示考虑 \(x\) 子树内的点，\(x\) 是/否可以和它的父亲连边。

转移考虑：

\[f_{x,0}=\sum_{y \in son(x)} \max(f_{y,0}+w(x,y),f_{y,1}) \]

\[f_{x,1}=\sum_{y \in son(x)} \max(f_{y,0}+w(x,y),f_{y,1}) \]

其中 \(f_{x,0}\) 选择的 \(f_{y,0}+w(x,y)\) 不能超过 \(k-1\) 个，\(f_{x,1}\) 选择的 \(f_{y,0}+w(x,y)\) 不能超过 \(k\) 个。

我们将 \(x\) 的儿子按 \(f_{y,0}+w(x,y)-f_{y,1}\) 排序，初始全选 \(f_{y,1}\)，然后选 \(f_{y,0}+w(x,y)-f_{y,1}\) 中前 \(k\) 大的即可。

这样做的复杂度为 \(O(n^2 \log n)\)。

然后进一步分析。

我们发现，如果当前的 \(k\) 很大，对于大部分点来说，它的所有边都是能被保留的，并且不随着 \(k\) 的值变化。

于是考虑我们将点按度数分为两类：\(deg_x \le k\)，称为一类点，\(deg_x>k\)，称为二类点。

有一个想法是，将一类点视为叶子，它们将二类点分割成了若干子树，这些子树都是独立的。

因为此时 \(x\) 的儿子大小是动态变化的，所以我们将排序改为在每个点维护一个堆。

从小到大枚举 \(k\)，我们需要分别决策三类贡献：

• 一类点对一类点：保留所有边，也就是做一个差分，预处理出两边度数都 \(\le k\) 的边的边权和。

• 二类点对二类点：根据上文所说，它们一定被划分到了一棵子树内，正常做就行；

• 二类点对一类点：因为我们将一类点视为叶子，那么它放进堆里的权值就是 \(w(x,y)\)。

实现上，我们只需要从二类点开始 dfs，如果 dfs 到了一类点，我们将 \(w(x,y)\) 放进父亲堆中并返回，并删去这条边，这样我们在以后的 DP 过程中不会再遇见它。

否则我们求解 DP 并将 \(f_{y,0}+w(x,y)-f_{y,1}\) 放进父亲堆中，将 \(f_{y,1}\) 累加到父亲的 DP 数组上。答案就是每个根的 \(f_{x,1}\) 之和，加上我们预处理的第一类答案。

然后注意我们每次 DP 结束时因为把二类点对一类点的边删了，所以我们不能把堆清空，只能清除二类点对二类点的边。我们对于堆中元素，维护边的种类，同时维护二类点对二类点的一个时间戳，这样就可以延时删除了。

删边按理说应该写链式前向星，但是 \(10^5\) 不怕多 log 就写了 set，这样好写多了。

千万注意不要每次都 dfs 一类点，这样做复杂度是假的。

现在分析复杂度。

设每次计算时二类点的个数为 \(cnt\)，那么单次计算我们的复杂度是 \(O(cnt \log^2 cnt)\)，又因为 \(\sum cnt=\sum deg=2n-1\)，所以我们总体复杂度为 \(O(n \log^2 n)\)。

总结：小清新 DP 优化，这个点度数均摊复杂度有点意思。都说这个题好口胡难写，我觉得想要把细节都处理清楚的话应该是难口胡好写吧。哎哎怎么两个小时了。

2022

14+60+100，线下银，线上银。

补题进度：14+100+100。

A

没读懂题。

读懂题了，直接状压原图可以获得 14 分的高分。

草正解怎么这么抽象，这我补啥啊，润了算了。

B

只会无脑分怎么办。

考虑如何刻画一个含有关键点的环，我们可以从某个点出发，经过若干条边到关键点的链上，然后再从链上某个点走回来。

一个点到链上，一定是链的一个前缀，链上到一个点，一定是链的一个后缀。

于是我们可以想到维护每个点到链上的前缀位置和后缀位置，分别记为 \(pre_i\) 和 \(suf_i\)，如果 \(pre_i \ge suf_i\)，那么一定有环，否则一定没有。

每次加边在原图和反图上做一个加边 dfs，同时做一个剪枝，如果我们当前点的 \(pre\) 或者 \(suf\) 没有被更新，那么我们就返回。因为我们本质不同的 \(pre_i\) 和 \(suf_i\) 只有 \(O(k)\) 个，所以这样做的复杂度为 \(O((n+m)k)\)，可以获得 60 分的高分。

实在不会了，来看题解。这是人能想到的吗。

考虑因为 \(pre\) 和 \(suf\) 不好维护，所以我们就不维护了（？）

因为我们最终关心的是 \(pre\) 和 \(suf\) 的相对关系，所以我们给每个 \(pre\) 和 \(suf\) 选取线段树上一个极短的，包含 \([pre,suf]\) 的节点，并且就把它当成原来的 \(pre\) 和 \(suf\)，这样我们判定是否有环，只需要考虑是否有线段被放到了叶子节点上。

考虑 \(x \to y\) 的实质，相当于 \(suf_x \to \min(suf_x,suf_y),pre_x \to \max(pre_x,pre_y)\)，于是我们考虑把这个东西推广到线段树上：

• \(suf_y \le pre_x\)，一定有环；

• \([pre_y,suf_y] \subseteq ls[pre_x,suf_x]\)，\([pre_x,suf_x] \leftarrow ls[pre_x,suf_x]\)；

• \([pre_x,suf_x] \subseteq rs[pre_y,suf_y]\)，\([pre_y,suf_y] \leftarrow rs[pre_y,suf_y]\)；

在进行 \(x\) 或 \(y\)，更新之后，我们需要遍历 \(x\) 或 \(y\) 的所有入边和出边递归更新，和之前 dfs 的过程是相似的。

这样每次更新区间长度减半，总复杂度为 \(O((n+m) \log k)\)。

总结：首先这个均摊复杂度分析就很有意思，这个记录近似值减少更新次数更厉害，感觉是一类很好的思想，不过很难想到就是了。

C

首先读完题应该就会 \(m \le 120\)。

考虑从小到大加数，每次将数放到开头，递增子序列个数 \(+1\)，放到结尾，递增子序列个数 \(\times 2\)。

然后递归构建排列即可，这样排列长度不会超过 \(2\lfloor \log n \rfloor\)。

实现这个做法应该有 90 分的高分。

然后我们进一步考虑，我们排列长度的更准确的值为 \(\lfloor \log n\rfloor+\text{popcount(n)}\)。

所以，我们每次只删去一个 \(1\) 是排列长度超限的主要原因，同时发现只要我们能够将相邻的两个二进制 \(1\)，每次用一次操作解决，那么我们就能构造出长度合法的排列。

于是我们的问题变成了，怎么做才能让递增子序列个数能够做到每次 \(+3\)。

其实很简单，考虑我们初始构造一个长度为 \(2\) 的递减序列，每次将数插入到前两个数后面，子序列数量正好 \(+3\)。

于是我们递归构建即可，注意这样做初始子序列个数为 \(3\)，需要特判 \(n=2\) 和 \(n=4\) 的情况。

总结：挺有意思的构造题，不是很难想到，但是最后 \(m=120 \to 90\) 我总觉得有随机化做法。

2023

100+40+4，线下铜，线上银。

补题进度：100+100+4。

A

看到每次除以 \(2\) DNA 动了。

考虑建立分层图，\((x,i)\) 表示使用了 \(i\) 次除以 \(2\) 操作，在 \(x\) 点。

跑以 \(n\) 为终点的最短路，那么有清零能力的点是起点。

然后考虑对于能除以 \(2\) 的点 \(x\)，我们可以松弛如下：

• \((x,i) \to (y,i)\)，\(dis_y=dis_x+w\)；

• \((x,i) \to (y,i+1)\)，\(dis_y=\frac{dis_x+w}{2}\)。

但是这个第二个转移看起来就很危险，因为我们可能一直向下松弛，dijsktra 提前把不该弹出的点弹出了，而当时已经是 2023 年不能写 spfa。

所以我们强制每次在上一层的点没有全部弹出之前，不能弹出下一层的点，这样就没问题了。

复杂度 \(O(km \log km)\)。

总结：没啥好总结的。成功签到。

B

首先看到给了 \(O(nv\log n)\) 不少分，推测可能和正解有关。

于是我们枚举中位数 \(x\)，将序列上的数分为三类：

• \(<x\) 的数，个数记为 \(w(l,r,0)\)；

• \(=x\) 的数，个数记为 \(w(l,r,1)\)；

• \(>x\) 的数，个数记为 \(w(l,r,2)\)。

考虑 \(x \in S(l,r)\) 的条件是什么。

我们有一个想法是：

\[|w(l,r,0)-w(l,r,2)| \le w(l,r,1) \]

于是我们的答案就是满足上面的条件的区间 \([l,r]\) 中，\(w(l,r,1)\) 的最大值。

扫描右端点，线段树简单维护即可做到 \(O(nv \log n)\)。获得了 40 分的高分。

然后实际上我就不会做了……于是开始翻讨论区，发现进一步的思路可能是扔到二维平面上。

那我们还是考虑这个式子：

\[|w(l,r,0)-w(l,r,2)| \le w(l,r,1) \]

实际上感觉带着绝对值太难受了，所以我们把绝对值拆了：

\[\max(w(l,r,0)-w(l,r,2),w(l,r,2)-w(l,r,0)) \le w(l,r,1) \]

\[\max(w(l,r,0)-w(l,r,2)-w(l,r,1),w(l,r,2)-w(l,r,0)-w(l,r,1)) \le 0 \]

到这里不难想到一个不成熟的思路：

我们令 \(x_l=w(1,l,0)-w(1,l,2)-w(1,l,1),y_l=(1,l,2)-w(1,l,0)-w(1,l,1)\)，那么区间 \([l,r]\) 合法当且仅当 \((x_{l-1},y_{l,-1})\) 在 \((x_r,y_r)\) 的右上方（含端点）。

这个看起来就很有前途，于是我们继续想下去。

我们因为还是扫描线，所以考虑 \((x_r,y_r) \to (x_{r+1},y_{r+1})\) 会产生什么变化：

• \(a_r=0\)，点向右下方移动一格；

• \(a_r=1\)，点向左下方移动一格；

• \(a_r=2\)，点向左上方移动一格。

也就是说：

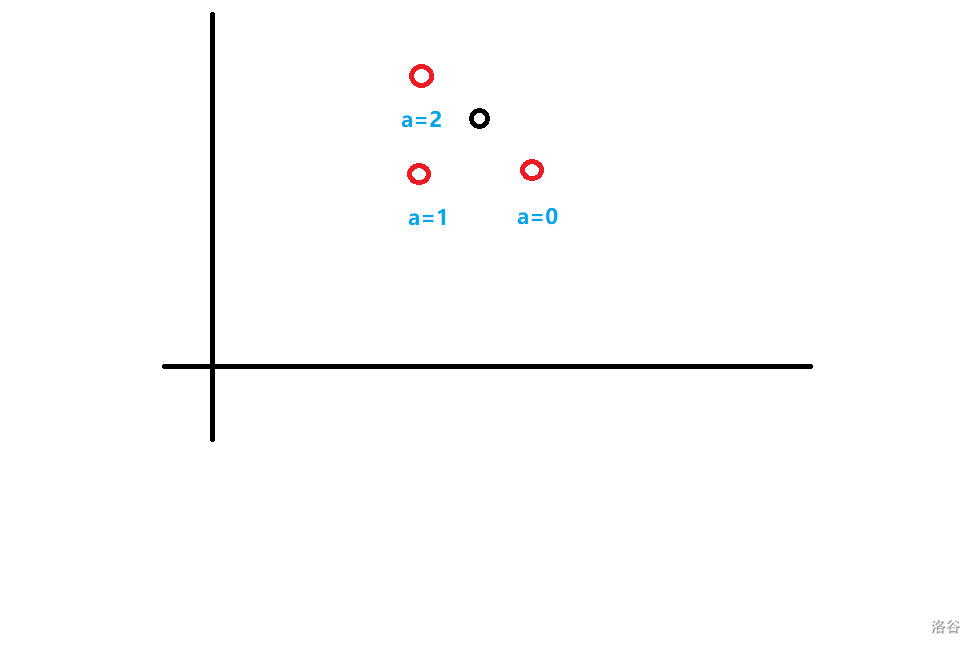
继续观察，发现整个图是若干条斜率为 \(-1\)，截距从 \(0\) 开始递减的线段，每条线段代表了被 \(a_i=1\) 划分的连续区间。

继续考虑图上的两条线段，上面的线段上选一个点，下面的线段上选一个点，那么只要这两个点满足之前所说的左上右下关系，那么答案就可以是这两条线段的截距之差。

用更直观的语言来说明，设上方线段左右端点的横坐标分别为 \(l_1,r_1\)，下方线段左右端点的横坐标分别为 \(l_2,r_2\)，那么我们只需要满足：

\[\begin{cases}l_2 \le r_1 \\ l_1 \le r_2\end{cases} \]

所以我们只需要求出线段的左右端点，就能扫描线求出答案。因为线段的总数是 \(O(n)\) 的，所以这一部分的复杂度是 \(O(n \log n)\)。

现在考虑线段的左右端点，实际上就是原序列上，连续段区间的的前缀最小值和前缀最大值。我们维护一棵支持单点修改，查询前缀最小值和前缀最大值的线段树即可，因为线段的总数是 \(O(n)\) 的，所以修改和查询的总数也是 \(O(n)\) 的，所以这一部分的复杂度也是 \(O(n \log n)\)。

总体复杂度 \(O(n \log n)\)。

总结：神仙题，也算是没看题解切题。前 40 分是套路，枚举中位数然后扫描线求解，后面构造二维平面上分析实在是太神仙了，没有明显提示根本想不到。整个思路很连贯很自然。我感觉评黑不过分。

C

快进到你读完题拿了 4 分。

不会了。

没题解我也会不了啊。

2024

100+10+100，银。

补题进度：100+100+100。

A

来搞笑的不是。

首先考虑原序列有若干合法的前缀，我们说一个前缀合法，当且仅当：

• 对于 \(m\) 个人，他们的前缀集合相同；

• 不存在非叶子节点被删除。

第一个条件可以用桶维护出现次数非 \(0\) 非 \(m\) 的节点。

第二个条件可以在不合法的删除节点打上标记，删除一个节点是找它能够删除的祖先节点，依次撤销标记并删除，记录当前存在的标记个数即可。

对于每一个合法的前缀，我们都可以把它作为一个划分点，不难发现这满足了答案上界。

总结：成功签到。

B

太困难。

首先读完题有了一个 \(O(n^2)\) DP 的做法，搭配 \(w=0\) 可以获得 10 分的低分。

然后发现这个 DP 可以按点的度数根号分治，使用 log 数据结构维护，做到 \(O(n \sqrt{n \log n})\)，可以获得 10 分的低分。

查看题解后发现自己脑子有问题……怎么是决策单调性来着。

我们重新考虑原 DP，设 \(f_i\) 表示经过第 \(i\) 条边的最小代价，那么有转移：

\[f_{i}=\min_{x_i=y_j,b_j \le a_i}f_j+w(b_j+1,a_i-1)t_{x_i}+c_i \]

其中 \(w(l,r)\) 表示被 \([l,r]\) 完全包含的线段个数。

然后这个 \(w\) 不难看出来满足四边形不等式，但是我就是没看出来。

于是考虑在每个点开一个单调队列维护 DP 值。具体来说，我们将边按 \(a_i\) 排序，每次在 \(x_i\) 单调队列中求出答案，然后挂到 \(b_i\) 上，到 \(b_i\) 时刻再把它放到 \(y_i\) 的单调队列里面。

这里的单调队列就是决策单调性的正常二分队列，不再赘述。

现在考虑 \(w(l,r)\) 的计算，还是考虑把线段挂到右端点上，每次在左端点加 \(1\)，查询前缀和。因为需要在线做，所以用主席树即可。

注意把时间离散化，不然很容易被卡。

复杂度 \(O(n \log^2 n)\)。

总结：的确没做过啥决策单调性的题，DP 优化光想 ds 优化了。

C

还是通信题好玩。

我们考虑树形结构是一个很重要的提示，树有很多种构建方式，我们先猜测最常见的一种：每个节点向编号小于自己的节点连边。

因为 C 删除的边的个数实在是太多了，所以感觉和整体树的形态相关的做法都很困难，于是我们只考虑连边节点之间带来的信息。

因为我们想要传递的是一个数，尝试和外星人进行沟通后，我们有了一个奇思妙想：\(i \to x \bmod i\)，我们发现这样构造恰好满足的树的限制，又给 B 传递了 5000 个同余方程，即使 C 删去其中的一半，B 也能轻松从剩下 2500 个中，exCRT 出 \(x\) 的值。

实际上，取 \(n=60\) 即可通过原题数据，这个交互库有点菜。

总结：很好玩的题，但是放到比赛中就是随机区分。