C++-纸牌金字塔 解题思路

【Horn Studio】编程专栏：纸牌金字塔 解题思路

题目

题目描述

高度为1的纸牌金字塔是通过将两张纸牌彼此相对放置而构成的。 对于h > 1，通过将高度为h-1的卡片金字塔放置在底座上来构建高度为h的卡片金字塔。底座由高度为1的h金字塔和顶部为h-1的卡片组成。 例如，高度为1,2和3的纸牌金字塔如下所示：

 

 

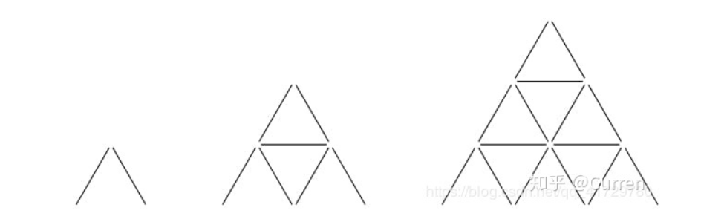
 您从N张牌开始，然后建造最高的金字塔。 如果有剩余的纸牌，则可以使用剩余的纸牌建立最高的金字塔。 您重复此过程，直到不可能建造另一个金字塔。 最后，您将建造多少座金字塔？

 

输入

第一行一个整数t表示数据组数(1≤t≤1000)(1≤t≤1000)

每组数据一行包括一个整数n表示纸牌的数量。(1≤n≤1e9)(1≤n≤1e9)

输出

每组数据一行表示答案

样例输入 复制

5
3
14
15
24
1

样例输出 复制

1
2
1
3
0

提示

来源

思路

乍一眼看来没有任何头绪，跟你说二分法你肯定也不信，但是，这道题真的是用二分，还十分简单……

先找找规律：

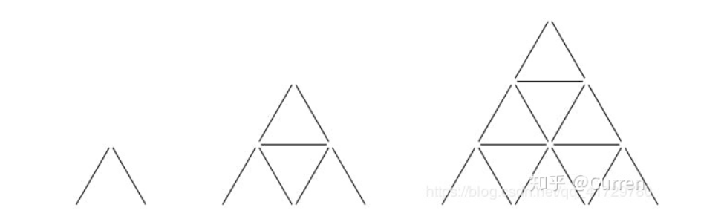
     （第一个：2，第二个：7，第三个：15），梦回dp算法，总结出来的规律是：

(1 + h) * h + h * (h - 1) / 2

有了这个就很简单了（忘了告诉你：十年OI一场空，不开Long long见祖宗）

接下来将木棍数二分，如果：

                long long mid = (le + ri) / 2;
                if (calNum(mid) > n) {
                    ri = mid - 1;
                } else {
                    res = max(res, calNum(mid));
                    le = mid + 1;
                }

然后综合一下代码，成了！

代码

#include <bits/stdc++.h>
using namespace std;

long long calNum(long long h)
{
    return (1 + h) * h + h * (h - 1) / 2;
}

int main()
{
    int t;
    cin >> t;
    while (t--) {
        long long n;
        cin >> n;
        long long cnt = 0;
        while (n >= 2) {
            cnt++;
            long long le, ri;
            le = 1;
            ri = n;
            long long res = -1;
            while (le <= ri) {
                long long mid = (le + ri) / 2;
                if (calNum(mid) > n) {
                    ri = mid - 1;
                } else {
                    res = max(res, calNum(mid));
                    le = mid + 1;
                }
            }
            n -= res;
        }
        cout << cnt << endl;
    }

}

彩蛋

冯子坤用C++做了个编程语言？！T237047 Horn Coding - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)