可持久化线段树
定义
建出的存储信息为不同版本情况的线段树（又称主席树）
核心思想
但直接每次复制一次，空间时间复杂度受不了
于是我们每次只新建有修改的点，没修改的直接连到老版本上
因此动态开点，记录新的根即可
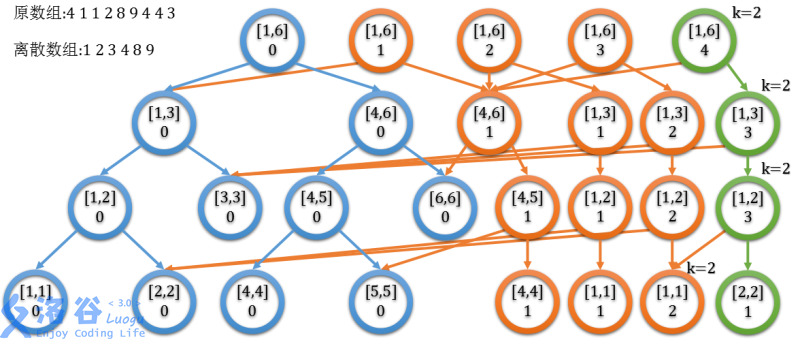
注意它“认子不认父”
时间空间复杂度均为 \(O(nlogn)\)
运用时要注意，找到前后序列的变化，
代码：
流程也跟着代码推出来
以P3919 【模板】可持久化线段树 1（可持久化数组）为例
0. 建树（有时可以省略）
inline ll build(ll l, ll r, ll p)
{
p = ++idx; // 开点
if(l == r)
{
tree[p] = a[l];
return p;
}
ll mid = (l + r) >> 1;
lc[p] = build(l, mid, lc[p]), rc[p] = build(mid + 1, r, rc[p]); // 单独用数组存子节点
return p; // 动态开点的线段树返回新开的节点
}
root[0] = build(1, n, 1); // main中
1. 修改
与以前的版本共同递归下去，先复制以前版本，再做修改，同时更新所在版本的根节点
inline ll update(ll last, ll id, ll val, ll l, ll r)
{
ll p = ++idx;
tree[p] = tree[last], lc[p] = lc[last], rc[p] = rc[last]; // 指向上个版本，复制上个版本的对应信息
if(l == r && l == id)
{
tree[p] = val;
return p;
}
ll mid = (l + r) >> 1;
if(mid >= id) lc[p] = update(lc[last], id, val, l, mid);
else rc[p] = update(rc[last], id, val, mid + 1, r, );
return p;
}
root[i] = update(root[ban], loc, val, 1, n, root[i]); // main
2. 查询
这里就跟普通线段树相同，\(p\) 一开始为查找的对应版本的根
inline ll query(ll id, ll l, ll r, ll p)
{
if(l == r && l == id) return tree[p];
ll mid = (l + r) >> 1;
if(mid >= id) return query(id, l, mid, lc[p]);
else return query(id, mid + 1, r, rc[p]);
}
应用
1. 静态区间第 \(k\) 大
这个题利用的是主席树维护信息的可减性
建可持久化权值线段树，对应权值离散化后在对应位置插入
从 \(1\sim n\)，每个位置都是一个版本，不用建树，修改相同
查询则类似于平衡树上找第 \(k\) 小的思想：直接在树上二分
当 \(tree[l[now]]-tree[l[pre]]\ge x\) 时，进入左边
这个式子的含义就是 \(l\sim r\) 区间中比 \(mid\) 小的数的个数
否则进入右边，注意 \(x\) 要减去左子树的节点数（同平衡树）
inline ll update(ll pre, ll id, ll val, ll l, ll r)
{
ll p = ++idx;
lc[p] = lc[pre], rc[p] = rc[pre], tree[p] = tree[pre] + val;
if(l == r && l == id) return p;
ll mid = (l + r) >> 1;
if(mid >= id) lc[p] = update(lc[pre], id, val, l, mid);
else rc[p] = update(rc[pre], id, val, mid + 1, r);
return p;
}
inline ll query(ll pre, ll noww, ll x, ll l, ll r)
{
if(l >= r) return l;
ll mid = (l + r) >> 1, res = tree[lc[noww]] - tree[lc[pre]];
if(res >= x) return query(lc[pre], lc[noww], x, l, mid);
else return query(rc[pre], rc[noww], x - res, mid + 1, r);
}
// main 函数中
for(reg ll i = 1; i <= n; ++i) root[i] = update(root[i - 1], lsh[a[i]], 1, 1, cnt);
for(reg ll i = 1; i <= m; ++i)
{
li = read(), ri = read(), ki = read();
print(rel[query(root[li - 1], root[ri], ki, 1, cnt)]), putchar('\n');
}
2. 找区间绝对众数
这里用到一个性质：（值域为 \(l\sim r\)，中间为 \(mid\)）
若有绝对众数，则在值域为 \(l\sim mid\) 或 \(mid+1\sim r\) 两段中一定有且仅有一段数的总个数大于总区间长度的一半
就转化为上面的题，建可持久化权值线段树查询每段中的数个数并判断，注意特判无解的情况
inline int update(int pre, int id, int val, int l, int r)
{
int p = ++idx, mid = (l + r) >> 1;
lc[p] = lc[pre], rc[p] = rc[pre], tree[p] = tree[pre] + val;
if(l == r && l == id) return p;
if(mid >= id) lc[p] = update(lc[pre], id, val, l, mid);
else rc[p] = update(rc[pre], id, val, mid + 1, r);
return p;
}
inline int query(int pre, int noww, int l, int r, int x)
{
if(l >= r) return l;
int mid = (l + r) >> 1, sl = tree[lc[noww]] - tree[lc[pre]], sr = tree[rc[noww]] - tree[rc[pre]];
if(sl > x) return query(lc[pre], lc[noww], l, mid, x);
if(sr > x) return query(rc[pre], rc[noww], mid + 1, r, x);
return 0;
}
// main 中
for(reg int i = 1; i <= n; ++i) a = read(), root[i] = update(root[i - 1], a, 1, 1, n);
for(reg int i = 1; i <= m; ++i)
{
li = read(), ri = read();
print(query(root[li - 1], root[ri], 1, n, (ri - li + 1) >> 1)), putchar('\n');
}
3. 在线找区间内某一值域内的数
仍然用前缀相减的思路，查出 \(1\sim r,1\sim l- 1\)
对每个前缀开权值线段树，再按序列下标可持久化
如果卡空间且可以离线，也可以用树状数组 + 扫描线
\(ans\) 的意思是当前没有被表示的最小数
如果区间内值在 \(1\sim ans\) 的数的和 \(tot\ge ans\)
意味着凑出 \(1\sim ans-1\) 后还有多余和 \(x\)， \(x=tot-(ans-1)\)
则 \(1\sim tot\) 都可以凑出，因为 \(ans\sim tot\) 中的数 \(-x\) 后在 \(1\sim ans-1\) 内，可以凑
那 \(ans\) 就变为 \(tot+1\)，直至 \(tot<ans\)，无法继续了
复杂度 ?
考虑从 \(ans\to tot+1\) 后又扩展一次
那么 \(1\sim tot+1\) 中数的和要 \(\ge tot+1\)，此时 \(1\sim ans\) 和为 \(tot\)
说明 \(ans+1\sim tot+1\) 中一定有数
那么 \(1\sim tot+1\) 中数的和即大于 \(2\times ans\)，\(ans\) 扩展两次至少翻倍
因此只会扩展 \(\log V\) 次
用主席树维护值域
inline int update(int pre, int id, int val, int l, int r)
{
int p = ++idx;
ls[p] = ls[pre], rs[p] = rs[pre], sum[p] = sum[pre] + val;
if(l == r) return p;
int mid = (l + r) >> 1;
if(mid >= id) ls[p] = update(ls[pre], id, val, l, mid);
else rs[p] = update(rs[pre], id, val, mid + 1, r);
return p;
}
inline int query(int pre, int nw, int l, int r, int nl, int nr)
{
if(l <= nl && nr <= r) return sum[nw] - sum[pre];
int mid = (nl + nr) >> 1, res = 0;
if(mid >= l) res += query(ls[pre], ls[nw], l, r, nl, mid);
if(mid < r) res += query(rs[pre], rs[nw], l, r, mid + 1, nr);
return res;
}
int main()
{
n = read();
for(reg int i = 1; i <= n; ++i) a[i] = read();
m = read();
for(reg int i = 1; i <= n; ++i) root[i] = update(root[i - 1], a[i], a[i], 1, inf);
for(reg int i = 1; i <= m; ++i)
{
li = read(), ri = read(), ans = 1;
while(1)
{
tot = query(root[li - 1], root[ri], 1, ans, 1, inf);
if(tot >= ans) ans = tot + 1;
else break;
}
print(ans), putchar('\n');
}
return 0;
}
4. 区间增加，之后找单点前 k 小
想对每个时刻维护以重要度为下标的权值线段树
但是空间不够，也不能一个个加入区间内元素
由于之后一次性询问，可以将区间差分，利用前缀相减，得到这个时刻的权值线段树
发现每个位置对上个位置，总共有 \(O(n)\) 个修改，可以用主席树维护
然后在主席树上二分即可
inline ll update(ll pre, ll id, ll val, ll l, ll r)
{
ll p = ++idx;
sum[p] = sum[pre] + val * id, num[p] = num[pre] + val, ls[p] = ls[pre], rs[p] = rs[pre];
if(l == r) return p;
ll mid = (l + r) >> 1;
if(mid >= id) ls[p] = update(ls[pre], id, val, l, mid);
else rs[p] = update(rs[pre], id, val, mid + 1, r);
return p;
}
inline ll query(ll p, ll k, ll l, ll r)
{
if(l == r) return min(k, num[p]) * l;
ll mid = (l + r) >> 1;
if(num[ls[p]] >= k) return query(ls[p], k, l, mid);
else return query(rs[p], k - num[ls[p]], mid + 1, r) + sum[ls[p]];
}
int main()
{
m = read(), n = read();
for(int i = 1; i <= m; ++i)
{
u = read(), v = read(), d = read();
lin[u].pb(mp(d, 1)), lin[v + 1].pb(mp(d, -1));
}
for(int i = 1; i <= n; ++i)
{
root[i] = root[i - 1];
for(pll j : lin[i]) root[i] = update(root[i], j.fi, j.se, 1, cnt);
}
for(int i = 1; i <= n; ++i)
{
xi = read(), ai = read(), bi = read(), ci = read(), ki = (ai * last + bi) % ci + 1;
last = query(root[xi], ki, 1, cnt);
print(last), putchar('\n');
}
return 0;
}
5. 找到相对上一位置变化较小的信息，维护
很有意思的题
首先发现直接优化不好做，这时一般考虑二分答案，发现答案确实有单调性
如果已知答案是 \(x\)，把 \(<x\) 的数看作 \(-1\)，\(\ge x\) 的数看作 \(1\)
如果左端点在 \([a,b]\)，右端点在 \([c,d]\) 的区间有和 \(\ge 0\) 的区间，那么就符合要求，否则不行
想到这我就一直在想随着每次二分的答案变化，感觉 \(-1,1\) 变化很多，不好维护
但是我忽略了：这是可以二分前预处理的！
如果把数按值从大到小排序，那么每个位置相对于前面总共只有 \(O(n)\) 个位置变化！
那么就可以主席树维护出这棵以序列位置为下标的线段树
维护区间和，前缀和的最大值，后缀和的最大值
inline int cmp(const int &c, const int &d)
{
if(c != d) return a[c] < a[d];
return c < d;
}
struct segt
{
int sum, ls, rs, lmx, rmx;
}tree[M];
inline segt pushup(segt p, segt lson, segt rson)
{
p.sum = lson.sum + rson.sum;
p.lmx = max(lson.lmx, lson.sum + rson.lmx), p.rmx = max(rson.rmx, rson.sum + lson.rmx);
return p;
}
inline int build(int l, int r)
{
int p = ++idx;
if(l == r)
{
tree[p] = (segt){1, 0, 0, 1, 1};
return p;
}
int mid = (l + r) >> 1;
tree[p].ls = build(l, mid), tree[p].rs = build(mid + 1, r);
tree[p] = pushup(tree[p], tree[tree[p].ls], tree[tree[p].rs]); return p;
}
inline int update(int pre, int id, int l, int r)
{
int p = ++idx;
tree[p] = tree[pre], tree[p].sum -= 2;
if(l == r)
{
tree[p].lmx = tree[p].rmx = -1;
return p;
}
int mid = (l + r) >> 1;
if(mid >= id) tree[p].ls = update(tree[pre].ls, id, l, mid);
else tree[p].rs = update(tree[pre].rs, id, mid + 1, r);
tree[p] = pushup(tree[p], tree[tree[p].ls], tree[tree[p].rs]); return p;
}
inline segt query(int p, int l, int r, int nl, int nr)
{
if(l <= nl && nr <= r) return tree[p];
int mid = (nl + nr) >> 1; segt res; res.ls = res.rs = 0;
if(mid >= l && mid < r)
{
res = pushup(res, query(tree[p].ls, l, r, nl, mid), query(tree[p].rs, l, r, mid + 1, nr));
return res;
}
if(mid >= l) return query(tree[p].ls, l, r, nl, mid);
return query(tree[p].rs, l, r, mid + 1, nr);
}
inline int check(int x)
{
ans = 0;
if(q[2] < q[3] - 1) ans = query(root[x], q[2] + 1, q[3] - 1, 1, n).sum;
ans += query(root[x], q[1], q[2], 1, n).rmx + query(root[x], q[3], q[4], 1, n).lmx;
if(ans >= 0) return 1;
return 2;
}
int main()
{
n = read();
for(int i = 1; i <= n; ++i) a[i] = read(), id[i] = i;
sort(id + 1, id + n + 1, cmp), root[1] = build(1, n);
for(int i = 2; i <= n; ++i) root[i] = update(root[i - 1], id[i - 1], 1, n);
Q = read();
for(int i = 1; i <= Q; ++i)
{
q[1] = (read() + las) % n + 1, q[2] = (read() + las) % n + 1;
q[3] = (read() + las) % n + 1, q[4] = (read() + las) % n + 1;
sort(q + 1, q + 5);
int l = 1, r = n;
while(l < r)
{
int mid = (l + r + 1) >> 1;
if(check(mid) == 1) l = mid;
else r = mid - 1;
}
las = a[id[l]], print(las), putchar('\n');
}
return 0;
}
6. 优化贪心过程
发现异或值最大？二进制下按位贪心是常见思路
但每次加上一个数，可持久化 trie 树不好做
假设现在从最高位开始取，发现贪心过程中前面的位已经固定了
想让当前位为 \(1\)，根据 \(x\) 的值也可确定这一位想要 \(0/1\)
也就是说，想要取的数的范围确定了
在 \([l,r]\) 内找有没有值域为 \([a,b]\) 的数，这就是主席树维护的经典问题
时间复杂度 \(O(q\log n\log V)\)
#include<bits/stdc++.h>
using namespace std;
const int N = 200010, M = 4000010, mx = 200001;
int n, m, a[N], bi, xi, li, ri, ans, idx, ll, rr, tot, sum[M], ls[M], rs[M], root[N];
inline int read()
{
char ch = getchar(); int x = 0;
while(ch < '0' || ch > '9') ch = getchar();
while(ch >= '0' && ch <= '9') x = (x << 1) + (x << 3) + ch - '0', ch = getchar();
return x;
}
inline void print(int x)
{
if(x / 10) print(x / 10);
putchar(x % 10 + '0');
}
inline int update(int pre, int id, int val, int l, int r)
{
int p = ++idx;
sum[p] = sum[pre] + val, ls[p] = ls[pre], rs[p] = rs[pre];
if(l == r) return p;
int mid = (l + r) >> 1;
if(mid >= id) ls[p] = update(ls[pre], id, val, l, mid);
else rs[p] = update(rs[pre], id, val, mid + 1, r);
return p;
}
inline int query(int pre, int nw, int l, int r, int nl, int nr)
{
if(l <= nl && nr <= r) return sum[nw] - sum[pre];
int mid = (nl + nr) >> 1, res = 0;
if(mid >= l) res += query(ls[pre], ls[nw], l, r, nl, mid);
if(mid < r) res += query(rs[pre], rs[nw], l, r, mid + 1, nr);
return res;
}
int main()
{
n = read(), m = read();
for(int i = 1; i <= n; ++i)
{
a[i] = read();
root[i] = update(root[i - 1], a[i] + 1, 1, 1, mx);
}
for(int i = 1; i <= m; ++i)
{
bi = read(), xi = read(), li = read(), ri = read();
ans = tot = 0, ll = rr = 0;
for(int j = 18; j >= 0; --j)
{
if((bi >> j) & 1) ll = ans - xi, rr = ans + (1 << j) - xi - 1;
else ll = ans + (1 << j) - xi, rr = ans + (1 << (j + 1)) - xi - 1;
ll = max(ll, 0), rr = min(rr, mx - 1);
if(query(root[li - 1], root[ri], ll + 1, rr + 1, 1, mx)) ans += ((bi >> j) & 1) ? 0 : (1 << j), tot += (1 << j);
else ans += ((bi >> j) & 1) ? (1 << j) : 0;
}
print(tot), putchar('\n');
}
return 0;
}
