《Pyramid Codes: Flexible Schemes to Trade Space for Access Efficiency in Reliable Data Storage Systems》金字塔码

第一部分：Introduction部分

问题1：Introduction部分，第五段，[16，12]ERC和3-Copy达到了相同的可靠性，在每一个块独立失败概率为0.01的情况下，这个是怎么证明的。

问题2：同上，第五段后半部分，那么多的IO次数是怎么计算出来的：5次读旧块（4个冗余+1个数据），5次计算恢复数据块，5次更新所有块。

在系统中，要分清各种性能指标，读和写是不一样的，第六段提到的是写性能，主要方法就是先用复制的方法增添冗余，然后等处理器负载低的时候，创建ERC，再把复制块删除，此时，存储降低（因为变为ERC存储到系统内），提高了写的性能（和复制方式的写性能一模一样），设计简单。

针对上述，什么是写入性能？我有了新的理解：就是当存数据的时候，好不好存的问题，再具体一点，复制方式存数据的时候，直接就存进去了，因为复制简单，所以写入很快；ERC方式存数据的时候，因为需要计算块，所以要磨磨唧唧的，就慢，同时也需要系统利用率。我们可以把写概括为计算+存储这个过程，同样的，读概括为存储取数据+计算为完整数据的过程。

同理，什么是读呢？其实就是DC数据收集功能，再直白一点，如果是复制块，那么直接读出来直接就可以用；而如果是ERC方法，读出来的是“零零散散的”，需要再拼装计算一下，才能得到完整的数据，所以读性能不如复制块的读性能。

现在有两个极端，一个是Copy方案，一个是ERC方案，这两个方案是两个极端，Copy是存储空间最大-访问效率最高，ERC方案是存储空间最小-访问效率最低，作者提出了自己的方案，可以在这两种之间自由的选择，都达到了最优的界。

 

 

第二部分：基本金字塔码

什么是MDS码呢？我之前的理解是Singleton界取等号的时候，其实有更简单的理解，就是n中的任意k个块，都可以还原出原始数据就OK，这样的理解更简单；按照这样的理解，所以复制方案其实也是MDS码，（1+r，1）MDS码；磁盘阵列RAID-5也是MDS码，是（k+1，k）MDS码。

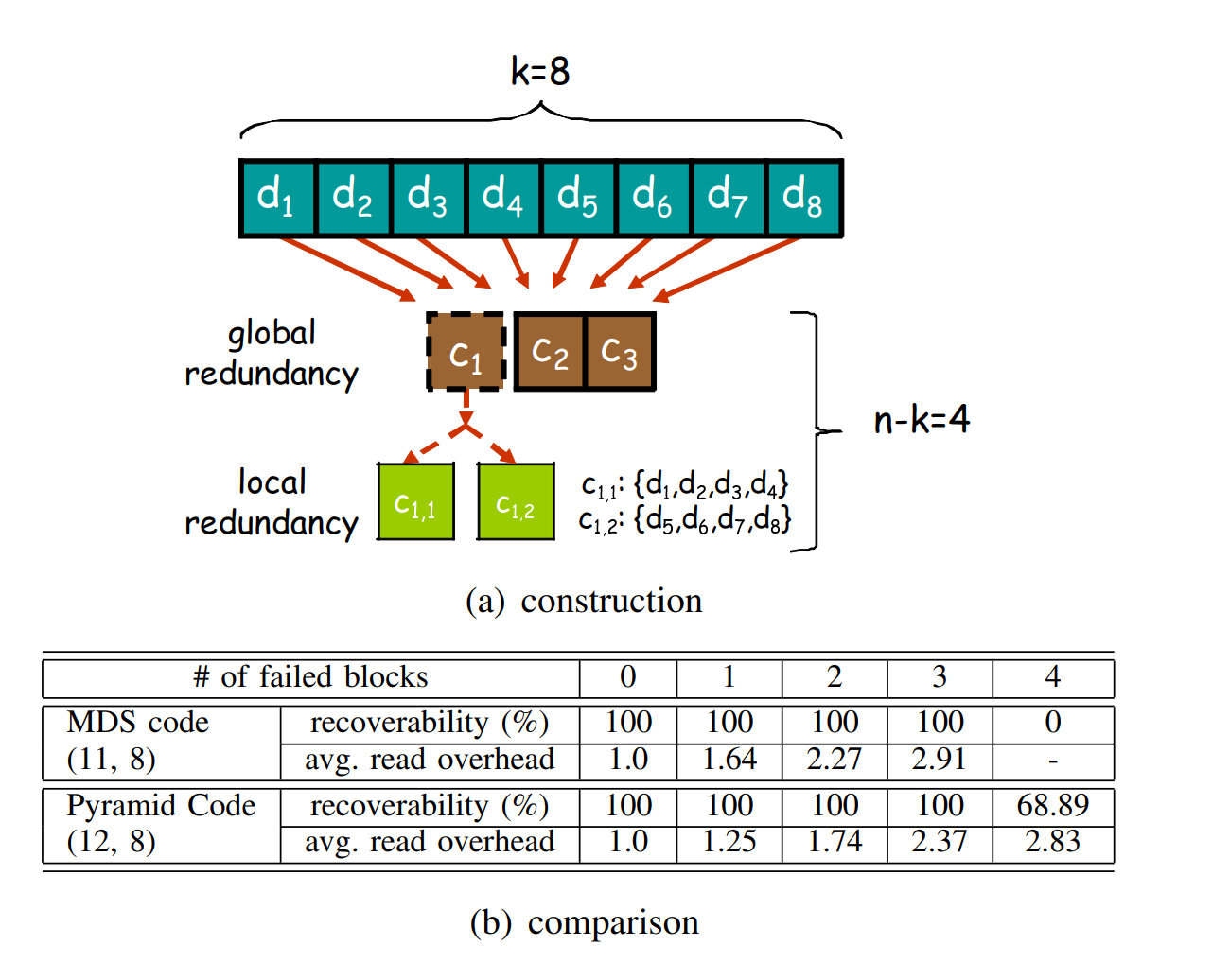
问题1：（11，8）MDS码是怎么添加冗余的，其实d1-d8是所有的数据块，可以保持不变的；然后c1-c3是根据d1-d8来增添冗余。当然，也可以把d1-d8变为c1-c11，这样计算量大，但是更加安全。

问题2：c1,1 c1,2合并后得到的c1，这个是怎么成立的，参考后面的生成矩阵的构造，其实就一切都明白了。

问题3：什么是MDS码？这个问题很傻逼，但是根据作者的描述，我又产生了疑惑。作者描述说，（11，8）的MDS码，假如发生了一位错误，假设错误在d1-d8中，那么读取开销为：d1-d8中的没有错误的7个+8，这个8是怎么来的呢，（答：由MDS的性质决定，任意的8个都能得到1个节点）我知道是通过MDS的属性而来，但是再具体一点说，MDS的属性难道不是说，n个块中，可以用任意的k个得到原始数据吗？在文章中，d1-d8都是数据块，没有编码过的，唯一的编码块是冗余块c1-c3，举例，假如d1错误，可以由d2-d8 ，再结合c1来生成d1，也可以d3-d8，再结合c1,c2,c3来生成，只要满足8个，就能完成恢复。

基本金字塔码的构造：先将数据分成L个不相交的组，记为S1,S2,... ,SL,其中每一个组包含kl个块；然后保持m1个冗余块中的m1不变，并且为每一个组sl计算m0 = m-m1个新的冗余块。

 

 

第三部分：广义金字塔码

为什么要提出广义金字塔码呢？图2介绍的很清楚：当一个组内，出现过多的失败时，能不能解决？该怎么解决呢？

能不能解决？（a）不能，如(a)所示，第一组内通过MDS属性是解决不了的，所以只能通过大的MDS属性来解决，d1-d12和c1,c2,c3,c4整个是[16,12]的MDS码，那么现在d7-d12（6个）c1,c2,c,3,c4这一共才10个，达不到12个，所以恢复不了。

（b）通过大的MDS也不能，因为d1-d4,d9,d10,d12，这是7个信息块，c3,c4这是2个冗余块，c2能通过c21,c22计算出来，这才10个，达不到12个，恢复不了。

（b）只能通过作者提出的广义金字塔码来恢复。所以当失败的块过多时，基本金字塔码没法解决该问题，只能通过整个码的MDS属性来解决（有时也解决不了），而非组内的MDS属性，这样的代价就是修复带宽和没有用金字塔码的带宽一样，所以广义金字塔码的作用就是解决这两个问题。（一个是修复不了；一个是修复带宽）

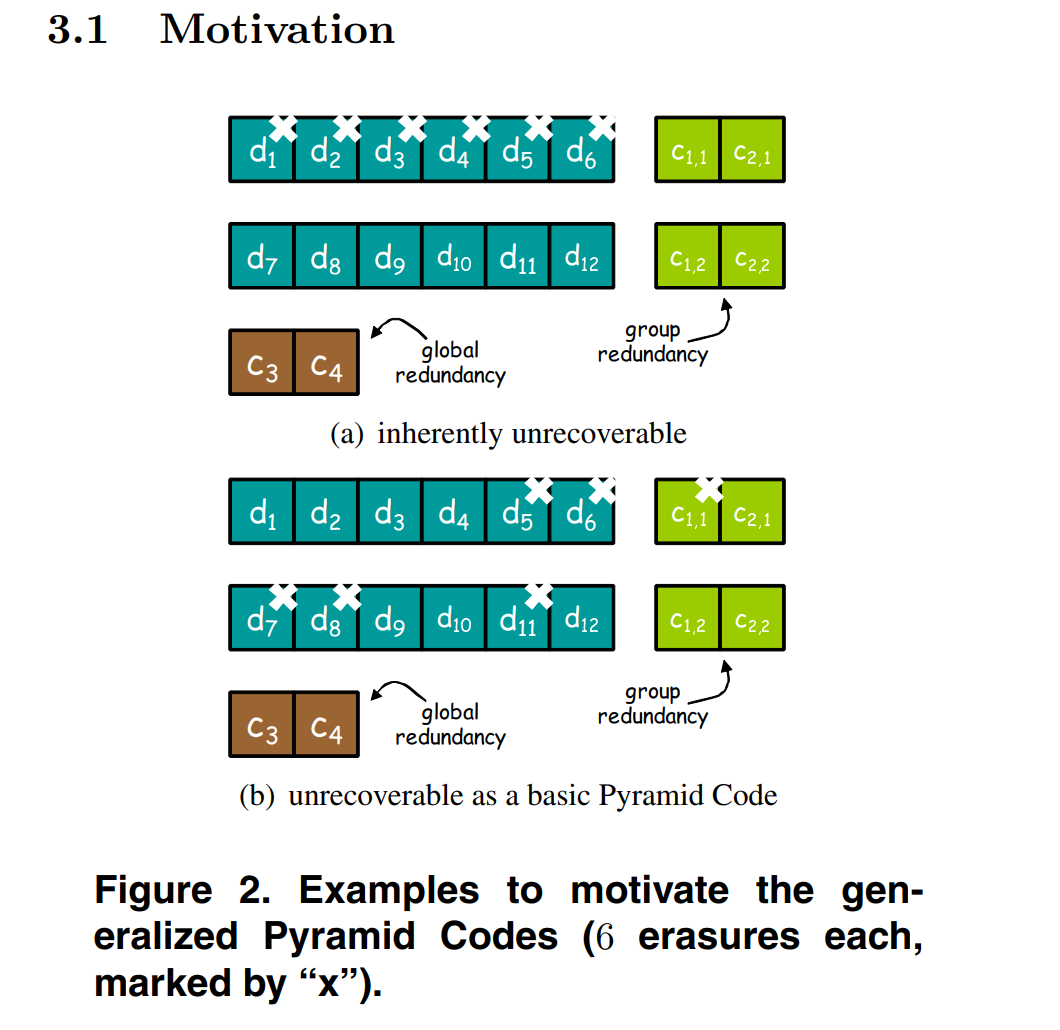
怎么解决呢？

通过我的学习，有两种，分别是（r，t）-locality和（r，δ）-locality，作者后面提出的抽象一下是（r，t）-locality，接下来详细说明。

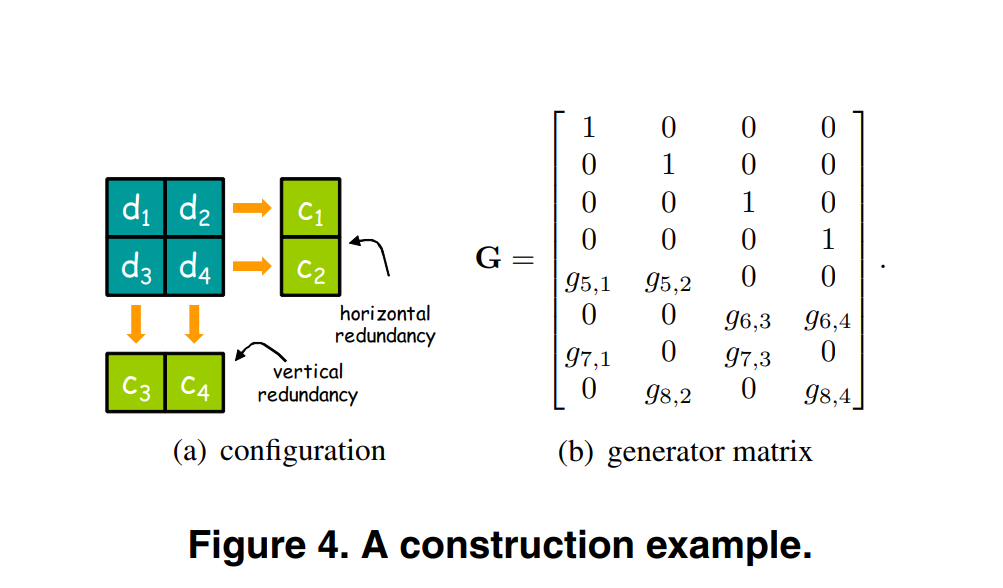
如上图4（a）所示，其实是（r，t）-locality，其中r=2，t=2，为什么这么讲呢？如下图（手写）所示，r=2是因为局部性为2，即如果d1出现失败，可以通过d2与c11来解决，需要两个节点的帮助，即r=2；t=2是因为可以有两种方法解决d1失败的问题，第一个是通过d2与c11，第二个是通过d3与c21来解决，所以t=2，假设也有斜着的块c31，c32，那么t=3（当然这种情况没有必要，这里只是举例）。

接着讲（r，δ）- locality方法，是右边的，其中c11和c12是d1与d2的冗余块，此时如果d1发生失败，那么可以通过第一组内的d2，c11,c12来恢复d1；假如d1，d2都发生错误（或者第一组中的任意2个发生错误），那么可以通过其他两个块解决，因为他们满足[4，2]MDS属性；r=2是因为局部性为2，即d1发生错误，任意两个都可以恢复；δ = 2是因为需要的冗余节点个数为2，以第一组为例，冗余节点分别是c11和c12，那么δ = 2 ，假如冗余节点个数变多时，那δ会变大。

 

 

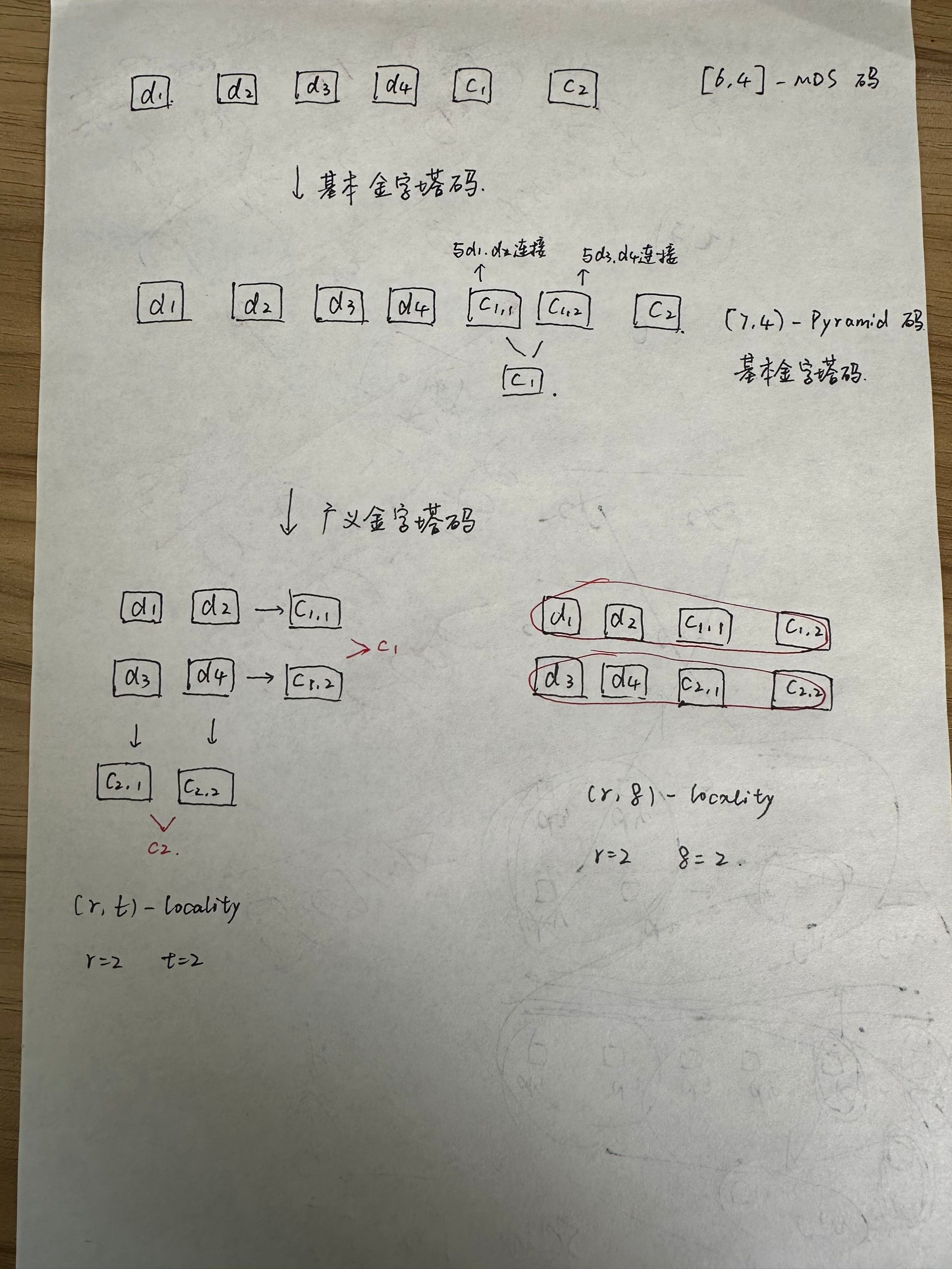
新的理解：

1.理解了什么是“金字塔”码，编码是从外到内，解码是从内到外，具体解释如下图：假设d1，d2，d3发生错误了，该怎么修复呢？最先判断的当然是用最小的修复代价来做，但是发现修复不了（即第一排蓝色框框修复不了）；然后用稍微大的框框（绿色）来修复，发现也修复不了，因为绿色框内满足[8，6]-MDS码，但是现在是3个错误，无法修复；再接着通过棕色的框框，即[16，12]-MDS码来修复，可以修复，修复的代价是多少呢？

这里要好好琢磨一下，用d4-d12，这是9个现成的块，还有c3，c4一共2个现成的块，c2需要通过两个绿色的块来组合，那么总共的代价是：9 + 2 + 2 = 13个块，也就是需要读13个块来修复d1；

现在d1修复好了以后，我们还需要通过同样的方法来修复d2吗？当然不用，我们可以用局部性来修复了：最小的蓝色框框还是不满足，绿色框框是满足的，代价是多少呢？d1 + d4 + d5 + d6 这是4个，两个蓝色组成c1,1 这是2个，绿色是1个，一共是7个块的读代价，也就是需要读7个块来修复d2，但是！问题来了，d4-d6我们是不是刚刚读了？那么此时我们还需要读吗？不需要，所以此时读的代价是7-3 = 4个。

现在d1，d2都修复好了，我们要修复d3，只需要用蓝色的局部性来做，具体来说，需要d1，d2，蓝色块，一共三个块，d1刚刚读了，不需要读，那么一共需要2个块；

这样是不是从外到内来解码呢？编码也是同样的道理。

 

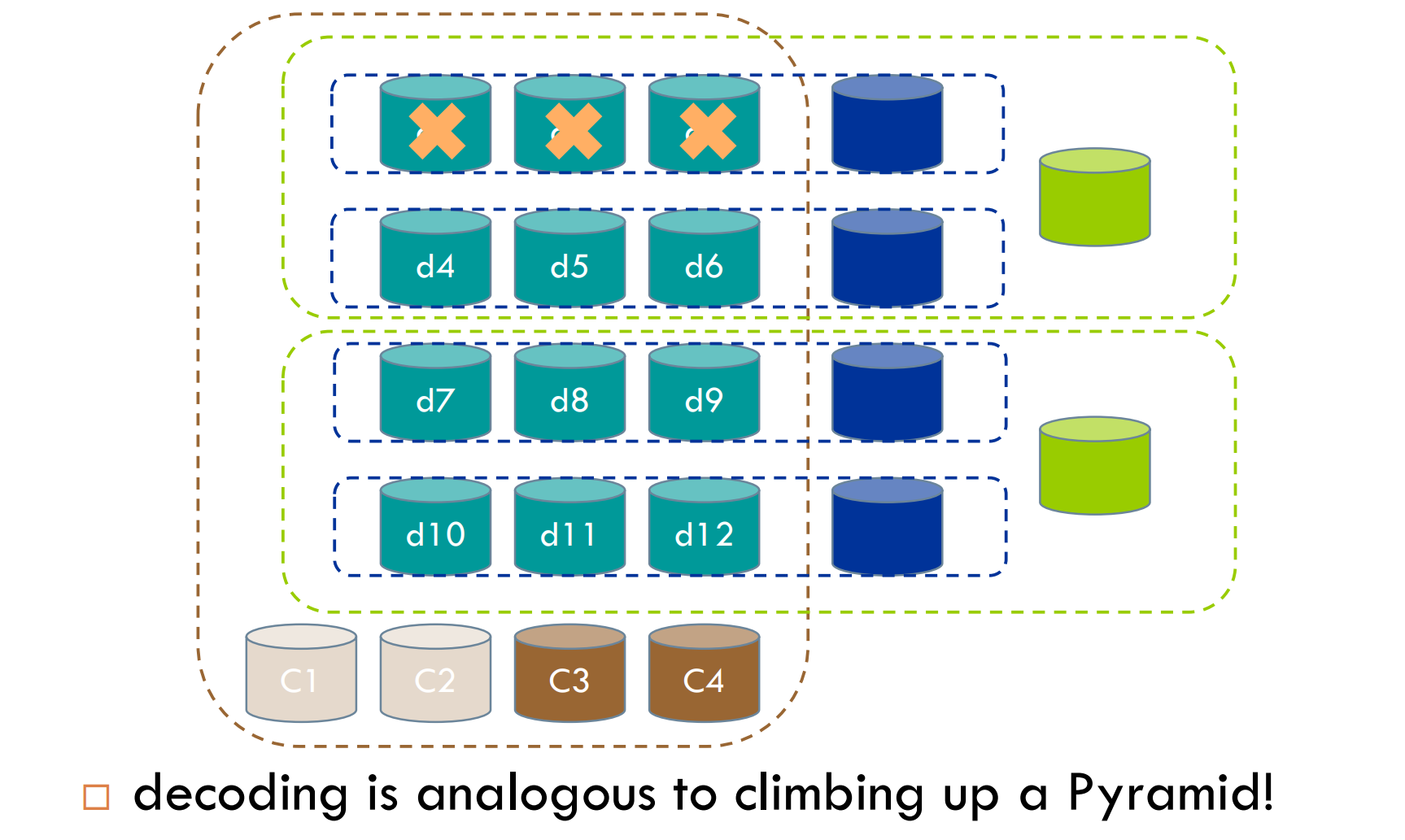
2.理解了DC数据收集和Repair数据修复的模型

就是在计算read代价那个部分，如下图，为什么MDS Code 或者 Pyramid Code 读的代价是这么大呢？我们来计算一下（当失败块=1时）

MDS：8/11的概率是数据块失败，此时先通过MDS属性修复失败的块，需要读任意的8个完成修复；然后再读剩下的7个块满足数据收集功能，此时一共读了7+8=15个块，平均8/11 * 15/8 = 11/15；3/11的概率是冗余块失败，此时不需要Repair，只用DC，代价=3/11；总的代价= 18/11 = 1.636 ，即1.64

Pyramid ：分情况，有8/12的概率数据块失败，此时需要：4个块的修复代价，再加上其他7个块的DC代价，总共=8/12 * （4+7）/8 = 11/12；如果是冗余块失败，则Reapair代价=0，直接DC，代价=4/12 *8/8 = 15/12 = 1.25

本质就是：如果有数据节点失败，先完成修复，再进行数据收集功能，这两个功能是分开的。（文章提到的模型如此，DC和Repair是分开的）